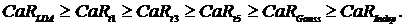Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Расчет величины рискового капиталаВ данном разделе рассмотрена реализация разработанной модели АМА на примере расчета капитала на покрытие операционного риска одного из кредитных банков средней величины. Будем в дальнейшем называть его - Банк. В качестве источников данных о потерях кредитных организаций, связанных с операционными рисками, была использована база ORX Analytics (далее - ORX), и консолидированные данные агентства Fitch. ORX - международная база данных, консолидирующая анонимную информацию о потерях операционных рисков, более чем 200 кредитных страховых и инвестиционных компаний из более чем 11 стран мира (ORX 2010). На основании данных ORX основными факторами операционного риска являются «Внешнее мошенничество» и «Внутреннее мошенничество» (более 75% убытков за последние 5 лет приходятся именно на них). Для демонстрации работы реализованного алгоритма АМА рассмотрена упрощенная модель симуляции убытков по трем следующим категориям риска: · «Внешнее мошенничество» (1); · «Внутреннее мошенничество» (2); · «Прочие» (3). Распределение величин убытков Оценка параметров Результат оценки параметров представлен в Приложении №4 «Оценка вероятностных распределений убытков» (таблица 4.1). Поскольку тесты Колмогорова-Смирнова и Андерсона-Дарлинга не могут быть использованы для распределений, превышающих установленный порог, выбор распределения порогового значения проводился на основе информационного критерия Акаике:  где L - значение функции максимального правдоподобия, q - число оцениваемых параметров распределения. На основании полученных результатов (таблица 4.1), логистическое распределение наилучшим образом описывает распределение порогового значения и. Таким образом, для моделирования величин убытков категорий 1-3 использована модель с логистическим распределением порога значимости и параметрами: Распределение частоты наступления убытков Оценка распределения частот наступления убытков по категориям 1-3 проводилась методом максимального правдоподобия в пакете MATLAB:
Для моделирования частот наступления убытков категорий 1-3 наилучшим образом подошли следующие вероятностные распределения:
Матрица Расчет величины ожидаемых убытков и рискового капитала Проведем дискретизацию полученного набора Расчет величины математического ожидания
Оценка коэффициента корреляции частоты наступления событий Матрица линейных корреляций Матрицы корреляций Моделирование набора частот для распределений Пуассона Первые три столбца матрицы Численный расчет корреляционного поля полученных зависимых процессов матрицы Freq_Mtrx эмпирически подтверждает разработанный алгоритм стохастического моделирования генерирования случайных процессов с предопределенной структурой зависимостей:
Средневзвешенное квадратичное отклонение составляет менее 4%, что обусловлено исключительно числом произведенных итераций:
Дискретизация вероятностного распределения Входными параметрами модуля FFT.m являются: · · На рисунках 5.1, 5.2 Приложения №5 «Стохастическое моделирование величины совокупного убытка» приведены 100 случайно выбранных траекторий совокупных значений величин убытков по каждой из трех категорий риска для случая независимых убытков и структуры зависимостей, определенной при помощи t-копулы Стьюдента (v=1). Оценка величины рискового капитала. Подходы LDA иАМА. Модель LDA В соответствии с упрощениями, предложенными Базельским Комитетом (Базель II) при реализации подхода LDA, использовано предположение о наличии идеальной корреляции между убытками, что позволяет получать величину совокупного рискового капитала К суммированием величин
При помощи аппроксимации (3.1) были получены оценки величин VaR в разбивке по категории риска • 250.2 млн. рублей для уровня значимости 99.9%; • 74 млн. рублей для уровня значимости 99.5%. Проверка адекватности полученных на основе аппроксимации (3.1) величин VaR для рассмотренного примера проводилась при помощи численного моделирования зависимых случайных процессов наступления убытков (с коэффициентом корреляции 1) и расчета величины рискового капитала на их покрытие на основе разработанного программного инструментария. Столбцы 4-6 матрицы Расчет величины VaR дискретного вектора вероятностного распределения В качестве аргументов в функцию CaR_Calculation.m последовательно передавались строки матрицы Данный алгоритм был проделан в цикле миллион раз Полученные результаты (Приложение №6 «Сравнение расчетных значений рискового капитала») свидетельствую о том, что при уровне достоверности близком к единице Модель АМА Расчет величины VaR в рамках подхода АМА также производился при помощи модуля CaR _ Calculation.m . В качестве аргументов в функцию CaR_Calculation.m последовательно передавались строки матрицы Алгоритм cтохастической модели Монте-Карло аппроксимации случайной суммы, был проделан в цикле миллион раз В таблице 2 представлено сравнение величин рискового капитала в разрезе по категориям риска, полученные для случая независимых распределений частот и для случая коррелированных убытков, моделирование которых осуществлялось при помощи копулы Гаусса и t-копул Стьюдента с v = 1,2,3 степенями свободы. Помимо расчета величины VaR, в модуле CaR _Calculation.m также реализован расчет показателя ES на основе меры риска Expected ShortFall, удовлетворяющей аксиомам когерентности. Детализированные результаты сравнения полученных расчетов приведены в Приложении №6 «Сравнение расчетных значений рискового капитала». Таблица 2.
В соответствии с результатами полученных расчетов величина принимает наибольшее значение при предположении об идеальной зависимости убытков (модель LDA, уровень значимости: 99.9%): 243,9 млн. рублей. Наименьшее значение величина Данный результат наглядно демонстрирует искомый эффект экономии рискового капитала за счет учета диверсификации рисков и полностью согласуется с теорией копул, выявляющей усиление структур зависимостей копул в последовательности: |
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 360. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
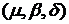 обобщенного распределения Парето при предположении о постоянном, нормальном и логистическом распределении порога значимости проводилась на основании алгоритма, описанного в главе 2 средствами MATLAB (Приложение №8 «Листинг MATLAB»).
обобщенного распределения Парето при предположении о постоянном, нормальном и логистическом распределении порога значимости проводилась на основании алгоритма, описанного в главе 2 средствами MATLAB (Приложение №8 «Листинг MATLAB»).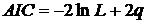 ,
,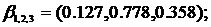
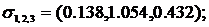
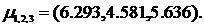
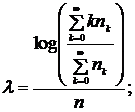
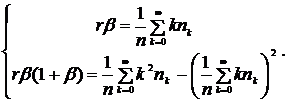
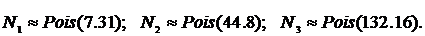
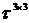 корреляций Кендалла частот наступления убытков категорий 1-3 приведена в таблице 4.2 Приложения №4.
корреляций Кендалла частот наступления убытков категорий 1-3 приведена в таблице 4.2 Приложения №4.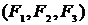 вероятностных распределений величины убытков методом взвешенного среднего. Шаг дискретизации h выбран равным 100 тыс. рублей, число точек дискретизации D выбрано равным 1048576 =
вероятностных распределений величины убытков методом взвешенного среднего. Шаг дискретизации h выбран равным 100 тыс. рублей, число точек дискретизации D выбрано равным 1048576 = 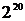 , так чтобы максимально возможный убыток (100 млрд. рублей РФ) заведомо превышал 99.9% квантиль распределения величины убытков.
, так чтобы максимально возможный убыток (100 млрд. рублей РФ) заведомо превышал 99.9% квантиль распределения величины убытков.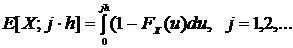 для каждого шага h производился численно средствами MATLAB. Листинг модуля дискретизации приведен в Приложении №8 «Листинг MATLAB».
для каждого шага h производился численно средствами MATLAB. Листинг модуля дискретизации приведен в Приложении №8 «Листинг MATLAB».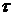 проводилась по формуле (исходя из определения):
проводилась по формуле (исходя из определения):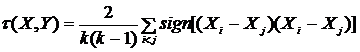 .
.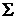 была получена из
была получена из 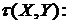
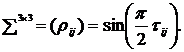
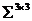 приведены в Приложении №4 «Оценка вероятностных распределений убытков» таблица 4.2.
приведены в Приложении №4 «Оценка вероятностных распределений убытков» таблица 4.2. , осуществлялось на основе копулы Гаусса и t-копул Стьюдента для 1-й, 3-х и 5-и степеней свободы (v=1,3,5). Число итераций М было выбрано равным 500тыс., 1 млн., 10 млн. В разделе 3.3 приведено исследование зависимостисходимости процесса Монте-Карло от числа итераций. Корреляционнаяструктура равномерно распределенных случайных величин в 2-х и 3-х мерномразрезе для различных копул приведена в Приложении №5 «Стохастическоемоделирование величины совокупного убытка». Листинг модуля генерацииматрицы Freq__Mtrx частот приведен в Приложение №8 «Листинг MATLAB»,(модуль Freq_Generation.m).
, осуществлялось на основе копулы Гаусса и t-копул Стьюдента для 1-й, 3-х и 5-и степеней свободы (v=1,3,5). Число итераций М было выбрано равным 500тыс., 1 млн., 10 млн. В разделе 3.3 приведено исследование зависимостисходимости процесса Монте-Карло от числа итераций. Корреляционнаяструктура равномерно распределенных случайных величин в 2-х и 3-х мерномразрезе для различных копул приведена в Приложении №5 «Стохастическоемоделирование величины совокупного убытка». Листинг модуля генерацииматрицы Freq__Mtrx частот приведен в Приложение №8 «Листинг MATLAB»,(модуль Freq_Generation.m).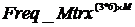 содержат набор независимых частот наступления убытков; следующие три столбца содержат набор идеально зависимых частот наступления убытков, полученных при помощи копулы Гаусса с единичной корреляционной матрицей и используемых для сравнения с результатами методики LDA; следующие три столбца (7-9) содержат набор зависимых частот, полученных при помощи копулы Гаусса и корреляционной матрицы
содержат набор независимых частот наступления убытков; следующие три столбца содержат набор идеально зависимых частот наступления убытков, полученных при помощи копулы Гаусса с единичной корреляционной матрицей и используемых для сравнения с результатами методики LDA; следующие три столбца (7-9) содержат набор зависимых частот, полученных при помощи копулы Гаусса и корреляционной матрицы 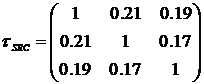 ;
; 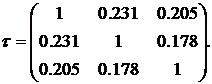
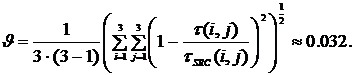
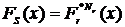 совокупной величины убытков
совокупной величины убытков 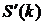 для каждой итерации t вычислялась при помощи модуля FFT.m (Приложение №8 «Листинг MATLAB»). При реализации функции FFT.m были использованы алгоритмы быстрого прямого и обратного преобразования Фурье.
для каждой итерации t вычислялась при помощи модуля FFT.m (Приложение №8 «Листинг MATLAB»). При реализации функции FFT.m были использованы алгоритмы быстрого прямого и обратного преобразования Фурье.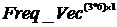 - t-вектор матрицы случайных частот наступления убытков по каждой их трех категорий риска и в разрезе 6 структур различных зависимостей
- t-вектор матрицы случайных частот наступления убытков по каждой их трех категорий риска и в разрезе 6 структур различных зависимостей 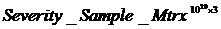 - матрица дискретных распределений величин убытков по трем категориям риска.
- матрица дискретных распределений величин убытков по трем категориям риска.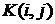 для каждой категории убытков
для каждой категории убытков 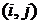 :
: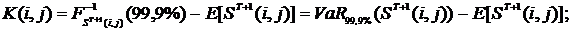
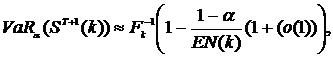 при
при 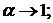 (3.1)
(3.1)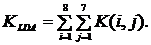
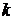 и по кредитной организации в целом:
и по кредитной организации в целом: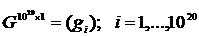 реализован в модуле CaR_Calculation.m (Приложение №8 «Листинг MATLAB»).
реализован в модуле CaR_Calculation.m (Приложение №8 «Листинг MATLAB»).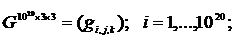
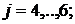
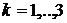 для каждой категории риска
для каждой категории риска 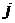 .
.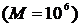 для каждого шага t смоделированных частот, затем полученные денежные эквиваленты квантилей по всем траекториям были сгруппированы по категориям риска, сложены и усреднены по числу итераций.
для каждого шага t смоделированных частот, затем полученные денежные эквиваленты квантилей по всем траекториям были сгруппированы по категориям риска, сложены и усреднены по числу итераций.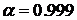 аппроксимация (3.1) может быть использована для оценки квантиля многомерной свертки независимых распределений (относительная погрешность
аппроксимация (3.1) может быть использована для оценки квантиля многомерной свертки независимых распределений (относительная погрешность 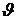 составляет 8.2 %). При
составляет 8.2 %). При 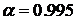 относительная погрешность
относительная погрешность 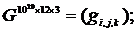
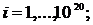
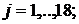
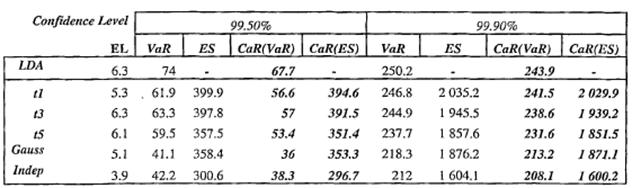 Сравнение расчётных значений капитала на покрытие операционного риска (млн. рублей).
Сравнение расчётных значений капитала на покрытие операционного риска (млн. рублей).