
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Моделирование зависимых структур случайных величин. Копульные функции.В задачах моделирования сложных зависимых структур и объектов, часто возникающих в финансовой и актуарной математике, особое место занимает аппарат копульных преобразований или копулы. По сути копулы позволяют моделировать многомерные распределения из одномерных с заранее установленными параметрическими зависимостями. Остановимся более подробно на основных фактах теории копул, использованных при построении модели. Виды зависимостей. Определение (Коэффициент линейной корреляции Пирсона Коэффициентом корреляции Пирсона двух случайных величин X, Y называется: Рассмотрим двумерное распределение случайных величин (X, Y):
Лемма (Верхняя и нижняя границы Фреше) Для любой двумерной функции распределения распределениями
Лемма (О симуляции случайных величин) Пусть
Данная Лемма позволяет моделировать выборку из любого вероятностного распределения при помощи набора равномерно распределенных случайных величин. Генератор псевдослучайных равномерных случайных величин реализован во всех современных компьютерах. Однако, корреляция Пирсона не сохраняется при обратном преобразовании. Для того чтобы генерировать случайные выборки из произвольных многомерных вероятностных распределений с предопределенной структурой зависимостей, необходимо использовать коэффициенты корреляции, не зависящие от самих вероятностных распределений. Корреляционными мерами являются коэффициент  Рассмотрим две пары непрерывных случайных величин Определение (Коэффициент Коэффициент зависимости т для пар
Определение (Коэффициент RankCorr (Spearman's rho)) Коэффициент ранговой корреляции Спирмена RankCorr равен: Определение (Коэффициент предельной зависимости Коэффициент предельной ("хвостовой") зависимости равен: Коэффициент предельной зависимости отражает вероятность того, что X будет «очень большой» при условии, что У- «очень большая», где «очень Большие» понимаются в терминах эквивалентных квантитлей соответствующих вероятностных распределений. Копульные структуры. Преобразование Холецкого Определение (Копула (Copula))[19] Копулой С называется совместное многомерное распределение Теорема Склара Для любой функции многомерного распределения Замечание Условие единственности Теоремы Склара выполняется только в случае непрерывных одномерных распределений. Остановимся более подробно на двух основных типах копул: экстремальные и эллиптических. Класс экстремальных копул включает следующие важнейшие копулы: При Эллиптические или неявные копулы получили наиболее широкое распространение в стохастической математике. В их основу заложены эллиптические распределения (многомерное нормальное, логнормальное, Стьюдента и др.). Рассмотрим вектор нормальных случайных величин
Разложим матрицу верхнетреугольной (транспонированной) матрицы В. Для симметричных и положительно определенных матриц, какими являются корреляционные матрицы, данное преобразование - преобразование Холецкого - всегда существует и единственно. Элементы матрицы В формируются по следующей реккурентной схеме:
Преобразование Холецкого позволяет получить наборы зависимых стандартно-нормальных и равномерно распределенных случайных величин (с матрицей корреляций случайных величин. Пусть величины. Тогда вектор Вектор случайных величин со структурой зависимости, определяемой матрицей Гауссова копула:
где
В случае нулевой корреляционной матрицы, Гауссова копула вырождается в независимую. Коэффициент
Коэффициент
t - копула Стьюдента:
где степенями свободы;
Коэффициент
Коэффициент предельной зависимости является однопараметрическим (параметр - число степеней свободы) и равен: Перейдем к описанию алгоритма стохастического моделирования зависимых случайных величин при помощи аппарата копульных функций. Алгоритм стохастического моделирования зависимых случайных величин. Алгоритм генерирования двух зависимых случайных процессов с известными параметрами распределения структурой зависимости 1. привести корреляцию Кендалла к линейной корреляции Пирсона; 2. выполнить преобразование Холецкого корреляционной матрицы 3. генерировать пару 4. получить пару 5. получить пару 6. выполнить обратное преобразование 7. повторить данный алгоритм, начиная с п.З В современных специализированных программных продуктах часть приведенных преобразований интегрированы в пакет расчета копул. В частности, в пакете MATLAB, использованного в работе, п.2-5 данного алгоритма объединены в рамках одной копульной функции: U = copulamd('Gaussian', Листинг программы приведен в Приложении «Листинг MATLAB». |
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 378. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
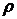 ).
).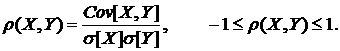

 с маргинальными
с маргинальными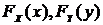 выполняется следующее неравенство:
выполняется следующее неравенство:
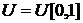 случайная величина, равномерно распределенная на [0,1]. Тогда кумулятивная функция распределения
случайная величина, равномерно распределенная на [0,1]. Тогда кумулятивная функция распределения  произвольной случайной величины X и
произвольной случайной величины X и 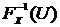 совпадают:
совпадают:
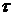 Кендалла и ранговая корреляция Спирмена
Кендалла и ранговая корреляция Спирмена 

 с маргинальными функциями распределения
с маргинальными функциями распределения 
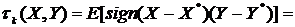


 )
)
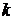 равномерно распределенных случайных величин:
равномерно распределенных случайных величин: 
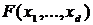 существует единственная копула
существует единственная копула  , такая что:
, такая что:  , где
, где  - соответствующие непрерывные одномерные функции распределения.
- соответствующие непрерывные одномерные функции распределения. - независимая копула;
- независимая копула; - нижняя граница Фреше;
- нижняя граница Фреше; - верхняя граница Фреше;
- верхняя граница Фреше;
 копула
копула 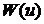 называется комонотонной (comonotonic copula).
называется комонотонной (comonotonic copula).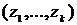 , состоящий из одномерных стандартно-
, состоящий из одномерных стандартно- с матрицей корреляций:
с матрицей корреляций: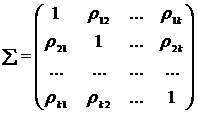
 на произведение
на произведение  нижнетреугольной и
нижнетреугольной и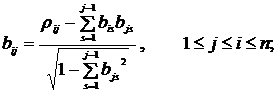
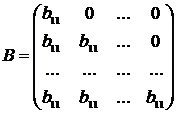 .
. - независимые стандартно нормальные случайные
- независимые стандартно нормальные случайные - задает
- задает  .
. задает набор из
задает набор из 
 - кумулятивная функция d -мерного нормального распределения;
- кумулятивная функция d -мерного нормального распределения;

 ,
,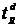 - кумулятивная функция d -мерного распределения Стьюдента с v -
- кумулятивная функция d -мерного распределения Стьюдента с v - - корреляционная матрица.
- корреляционная матрица.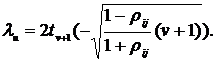
 и предопределенной
и предопределенной

 -независимых стандартно-нормальныхслучайных величин
-независимых стандартно-нормальныхслучайных величин 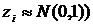 ;
; зависимых стандартно-нормальных случайныхвеличин
зависимых стандартно-нормальных случайныхвеличин 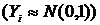 с параметром корреляции
с параметром корреляции  зависимых равномерно распределенныхслучайных величин с параметром корреляции
зависимых равномерно распределенныхслучайных величин с параметром корреляции  , получитьискомую пару (X,Y) - выборку из зависимых случайных процессов
, получитьискомую пару (X,Y) - выборку из зависимых случайных процессов 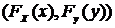 с параметром корреляции
с параметром корреляции  раз, для того чтобы получитьискомую выборку объемом
раз, для того чтобы получитьискомую выборку объемом  .
.
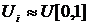 с корреляционной матрицей
с корреляционной матрицей