
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Расчет величины рискового капиталаОпределение Мерой риска на вероятностном пространстве В исследованиях, посвященных теории риска, широкое распространение получил класс когерентных мер риска, как класс функций наиболее адекватно описывающих процессы финансового мира, в т.ч. эффект диверсификации рисков (свойство субаддитивности). Определение Мера риска следующим свойствам: · Суббаддитвность: · Монотонность: · Положительная однородность: Замечание В определении когерентной меры риска присутствует условие инвариантности к сдвигу: Тогда: Определение Для заданного уровня достоверности называется: Замечание В общем случае мера VaR не является когерентной (не выполняется свойство субаддитивности). Рассмотрим следующий пример, демонстрирующий нарушение свойств когерентности, для меры VaR. Пусть и При Одновременно: Замечание Если квантили распределений вычисляются в предположении о совместно нормальном распределении, то мера риска VaR является когерентной (условия субаддитивности, монотонности, положительной однородности и  инвариантности к сдвигу выполняются). Определение (Expected ShortFall - ES) Для заданного уровня достоверности определенной в соответствии с вышестоящим замечанием, мерой риска ES (Expected Shortfall) называется условное математическое ожидание: Мера риска ES - является когерентной. В главе 3 приводится сравнения величин CaR, полученных с помощью ES и VaR для моделей АМА и LDA Когерентное распределение рискового капитала. Вектор Лумана-Шепли. Пусть, рассчитанная в соответствии с методикой LDA величина рискового капитала, на покрытие операционного риска i-ro подразделения или i-ro направления деятельности составляет: В соответствии с рекомендованной Базель II методикой LDA, суммарная величина капитала на покрытие операционного риска, рассчитывается как сумма капиталов по всем подразделениям:
Как видно из результатов сравнения величин капиталов, приведенных в главе 3, такой подход ведет к существенному завышению величины рискового капитала вследствие отказа от учета корреляции между рисками. Рассмотрим модификацию данного подхода, позволяющую учесть эффект диверсификации рисков на этапе их суммирования, без применения усложненных подходов, использованных в АМА. Зададим принцип распределения капитала между подразделениями (подпортфелями) организации функцией П:
Определение (компонентый VaR) Распределением капитала с учетом корреляции рисков подразделений (компонентый VaR) называется:
Однако, как было показано ранее мера VaR не отвечает условию субаддитивности, поэтому применение компонентного VaR также является нежелательным. Определим критерием эффективного распределения рискового капитала выполнение условий когерентности. Определение (Когерентное распределение капитала) Принцип распределения П капитала когерентен, если выполнены следующие свойства: 1. 2. Если при объединении произвольных подмножеств Распределение рискового капитала есть не что иное, как распределение затрат между несколькими подразделениями кредитной организации (игроками) с определенными ограничениями на вид меры риска (функции затрат) и некоторыми граничными условиями, поэтому кооперативная теория игр как нельзя лучше подходит для постановки задачи и получения конечных результатов. Перейдем к формулировке задачи когерентного распределения рискового капитала в терминах кооперативной теории игр Необходимые факты кооперативной теории игр[21] Пусть
Для когерентной меры риска функция затрат является субаддитивной: Определение (Ядро игры) Ядром игры 1. 2. Второе свойство означает, что коалиция никогда не заплатит цену, превосходящую те затраты, которые она понесет, если захочет обслуживаться самостоятельно. На вопрос наличия непустого ядра кооперативной игры отвечает критерий О.Н.Бондаревой, а также более сильное достаточное условие - условие субаддитвности игры: Встает вопрос: каким образом из ядра выбрать одно единственное распределение затрат, которое и будет искомым? Объект, ставящий в соответствие игре одно единственное распределение, называется значением или оператором значения.
Определение (Оператор значения игры) Оператор значения
В теории игр на множество операторов значения накладывают три следующих требования: 1. Симметричность: оператор значения 2. Аддитивность: 3. Аксиома «дурака»: Теорема (Л. Шепли) Существует только один оператор значения, удовлетворяющий свойствам симметричночти, аддитивности и аксиоме «дурака» - вектор Шепли:
Свойство аддитивности вектора Шепли дает следующий полезный результат: в случае, когда мера риска представляется суммой когерентных мер (например, рыночный плюс кредитный риск), для нахождения распределения с использованием вектора Шепли достаточно вычислить вектор Шепли для каждой из мер и затем их сложить. Таким образом, вектор Шепли, в случае его принадлежности ядру игры, задает единственный искомый принцип распределения рискового капитала. Достаточным условием принадлежности вектора Шепли ядру кооперативной игры является вышеуказанное условие супераддитивности игры. Однако известно, что игра, определяемая когерентной мерой риска, удовлетворяет условию супераддтивности только в случае линейных мер риска. Линейность влечет отсутствие эффектов диверсификации рисков, поэтому рассматривать такие меры в задаче распределения рискового капитала нецелесообразно. В классе кооперативных атомических игр задача когерентного распределения рискового капитала кредитной организации в общем случае решения не имеет. Было введено предположение ограниченности и неделимости множества подразделений (подпортфелей) N. Если отказаться от последнего требования (неделимости), то мы перейдем в более общий класс кооперативных игр - класс неатомических игр, для которых также существует обобщенный аналог вектора Шепли, который в свою очередь является единственным решением неатомической кооперативной игры и в, отличии от атомической игры, всегда принадлежит ее ядру. Неатомические кооперативные игры. Определим также как и в предыдущем разделе, конечное множество Определение Кооперативной неатомической игрой называется множество Функцию затрат коалиции
Определим оператор
Определение Оператор значения кооперативной неатомической игры 1. Обобщенная инвариантность: Если для мер риска матрицы 2. Непрерывность: отображение 3. Монотонность: пусть 4. Нечеткое ядро игры: отображение 5. Аксиома «дурака»: если 6. Оператор значения игры Теорема (Р.Ауман, Л.Шепли) Существует единственный оператор значения кооперативной неатомической игры, удовлетворяющий пяти аксиомам когерентности и принадлежащий ядру игры - вектор Аумана-Шепли: Для однородных мер риска (требование однородности меры является 3й аксиомой когерентности) вектор Аумана-Шепли удается выразить в явном виде: Величина (подпортфеля).
Таким образом, полученное аналитическое выражение вектора Аумана- Шепли, является искомым принципом когерентного распределения рискового капитала кредитной организации. Величина рискового капитала определяется как: Известно, что маргинальный риск меры VaR представляется в виде: Таким образом, при предположении о нормальном распределении риск-факторов принцип когерентного распределения рискового капитала соответствует концепции компонентного VaR: где
|
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 363. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
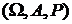 называется отображение
называется отображение 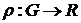 , где G - множество ограниченных функций над
, где G - множество ограниченных функций над 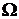 (множество элементарных событий), R - вещественная прямая.
(множество элементарных событий), R - вещественная прямая.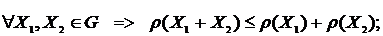
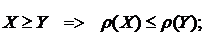
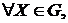
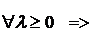
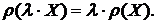
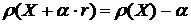 , где г - некоторый безрисковый инструмент. В настоящей работе это требование опущено, т.к. является несущественным для получения основных результатов и, более того, имеет нежелательные следствия. Например, из него следует, что когерентная мера риска не может быть суммой когерентных мер. Пусть
, где г - некоторый безрисковый инструмент. В настоящей работе это требование опущено, т.к. является несущественным для получения основных результатов и, более того, имеет нежелательные следствия. Например, из него следует, что когерентная мера риска не может быть суммой когерентных мер. Пусть 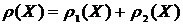 .
.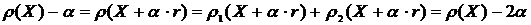
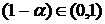 мерой риска VaR
мерой риска VaR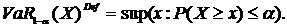
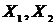 - независимые одинаково распределенные случайные величины, имеющие плотность вероятности 0.9 на отрезке [0, 1] и 0.05 на отрезке [-2, 0].
- независимые одинаково распределенные случайные величины, имеющие плотность вероятности 0.9 на отрезке [0, 1] и 0.05 на отрезке [-2, 0].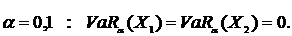
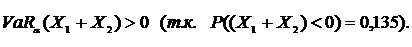
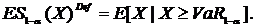
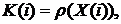 где
где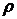 - одна из рассмотренных выше мер риска.[20]
- одна из рассмотренных выше мер риска.[20]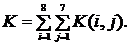
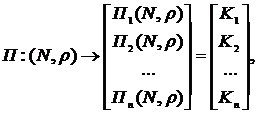 где
где 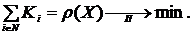 (2.9)
(2.9)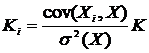
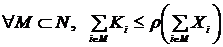 - свойство неотделимости.
- свойство неотделимости.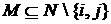 портфели
портфели 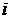 и
и 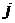 вносят одинаковый вклад в рисковый капитал, то
вносят одинаковый вклад в рисковый капитал, то 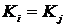 . (свойство симметричности).
. (свойство симметричности).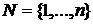 - конечное множество подразделений (подпортфелей). В рамках данного раздела, множество подразделений будем считать ограниченным и неделимым. Функция затрат c(S) определена на каждом подмножестве
- конечное множество подразделений (подпортфелей). В рамках данного раздела, множество подразделений будем считать ограниченным и неделимым. Функция затрат c(S) определена на каждом подмножестве 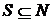 (называемом также коалицией) следующим образом:
(называемом также коалицией) следующим образом: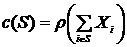
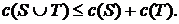
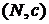 называется множество распределений
называется множество распределений 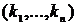 удовлетворяющих двум следующим свойствам:
удовлетворяющих двум следующим свойствам: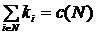 - (условие эффективности);
- (условие эффективности);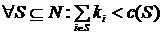 - (принцип отделения).
- (принцип отделения).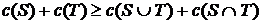 . На основании теоремы О.Н.Бондаревой известно, что в игре с функцией затрат, определяемой когерентной мерой риска, ядро не пусто.
. На основании теоремы О.Н.Бондаревой известно, что в игре с функцией затрат, определяемой когерентной мерой риска, ядро не пусто.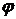 есть отображение
есть отображение 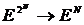 , ставящее в соответствие каждой игре (N, с) распределение
, ставящее в соответствие каждой игре (N, с) распределение 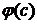 величины c(N), такое что:
величины c(N), такое что: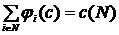 .
.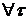 - биекции множества N в себя и
- биекции множества N в себя и 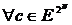 выполняется:
выполняется: 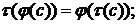
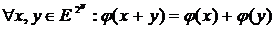 ;
;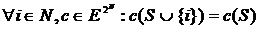
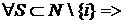
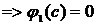
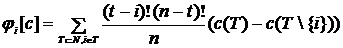 (2.10)
(2.10)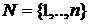 подразделений (подпортфелей). Предположим, что каждая коалиция может состоять из
подразделений (подпортфелей). Предположим, что каждая коалиция может состоять из 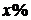 портфеля 1, у% портфеля 2 и т.д. Пусть компоненты вектора
портфеля 1, у% портфеля 2 и т.д. Пусть компоненты вектора 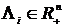 соответствуют возможным вкладам i-ro игрока (подразделения) в каждую коалицию.
соответствуют возможным вкладам i-ro игрока (подразделения) в каждую коалицию.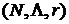 , где: N - конечный набор игроков, | N |= п;
, где: N - конечный набор игроков, | N |= п; 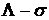 -алгебра над [0,1];
-алгебра над [0,1]; 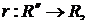
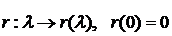 - функция затрат.
- функция затрат.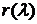 будем определять через когерентную меру
будем определять через когерентную меру 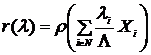 .
.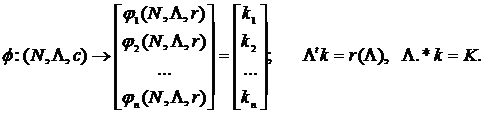
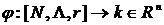 задает принцип когерентного распределения капитала, если для неговыполняются следующие 5 условий когерентности, и он принадлежит ядруигры:
задает принцип когерентного распределения капитала, если для неговыполняются следующие 5 условий когерентности, и он принадлежит ядруигры: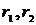 , некоторой
, некоторой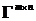 и
и 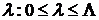 выполнено условие:
выполнено условие: 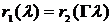 , то
, то 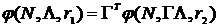 ;
;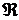 непрерывно дифференцируемых мер
непрерывно дифференцируемых мер 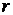 ;
;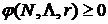 ;
;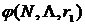 принадлежит ядру игры
принадлежит ядру игры 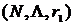 , если для всех
, если для всех 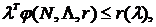
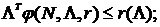
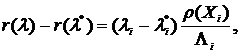 где наборы
где наборы 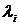 и
и 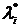 отличаются компонентом
отличаются компонентом 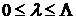 , то
, то 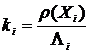 ;
;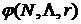 принадлежит ядру игры, если
принадлежит ядру игры, если 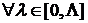 выполняется:
выполняется: 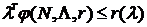 , при этом
, при этом 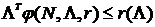 .[22]
.[22]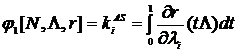 .
.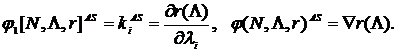
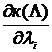 представляет маргинальный риск i-го подразделения
представляет маргинальный риск i-го подразделения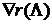 - градиент Аумана-Шепли функции затрат подразделения.
- градиент Аумана-Шепли функции затрат подразделения.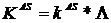 .
.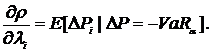
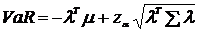 ,
,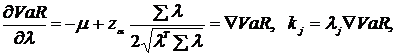
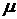 и
и 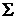 - математическое ожидание и матрица ковариации соответственно.
- математическое ожидание и матрица ковариации соответственно.