
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Моделирование величин убытковРаспределения величин убытков операционных рисков относятся к классу экстремальных. Накопленной кредитной организацией собственной статистической информации недостаточно для того чтобы оценить вид и параметры экстремальных распределений. Поэтому внутренняя информация о потерях должна быть дополнена масштабированными данными о потерях внешних кредитных организаций (внешними данными). При моделировании величин убытков использованы следующие утверждения и предположения:
Предположение 1 Выборки данных происходят из одних и тех же вероятностных распределений, но с разными порогами значимости для каждой организации.
Утверждение 1. Параметр значимости потерь - случайная величина (минимальное значение величины потерь, начиная с которого кредитная организация предоставляет информацию) может быть достоверно оценена методами Теории Экстремальных Значений (EVT).[16]
Утверждение 2. Распределения величин операционных потерь принадлежат области притяжения семейства распределений Фреше. Таким образом, их условное превышение заданного порогового значения может быть аппроксимировано через обобщенное распределение Парето.
Мэппинг внешних данных. Рассмотрим две независимые случайные величины случайной величины х порогового значение
где Воспользуемся следующими фактами EVT :
Определение (Maximum Domain Attraction - MDA) Пусть H(x) - невырожденная функция распределения. Будем говорить, что функция распределения F(x) принадлежит области притяжения Н(х), если  существуют последовательности Теорема Фишера-Типпета (Об аппроксимации максимумов Н.О.Р.С.В)[17] Если предельное распределение максимумов независимых и одинаково распределенных случайных величин (Н.О.Р.С.В.) не вырождено для некоторой последовательности
Теорема Балкена-де-Хана Пекандса (Об аппроксимации условных превышений Н.О.Р.С.В.) (Упрощенная формулировка)[18] Для некоторого фиксированного порогового значения условное распределение максимумов Н.О.Р.С.В. принадлежит области притяжения семейства распределений Фреше. Таким образом, приведенные факты EVT и результаты исследований позволяют в дальнейшем воспользоваться Утверждением 2 (плотность распределения величин наблюдаемых внешних убытков может быть аппроксимирована распределениями семейства Фреше). Пусть L - величина совокупного убытка, зафиксированного с порогом Плотность распределения условной вероятности (2.3) превышений наблюдаемой случайной величины х порогового значение h можно переписать в следующем виде: при предположении о нормальном распределении порогового значения:
при предположении о нормальном распределении порогового значения:
Для того чтобы учесть временную стоимость денег (привести к одной стоимости убытки, произошедшие в разные моменты времени) используем в качестве дисконтирующего множителя бескупонную кривую однолетних ставок Libor, действующих с момента наступления. Пусть убыток величины
Нижняя граница условных убытков, превышающих порог и , имеет вид:
Таким образом, плотность распределения условной вероятности (2.3) будем рассматривать на полуотрезке: Приведем краткое описание итерационного вычислительного алгоритма оценки параметров Оценка параметров. Для некоторой фиксированной категории риска Преобразуем вектор
Используя метод максимального правдоподобия (ММП), получаем:
Заменим
Знаменатель формулы (2.5) представляет свертку распределений, последовательный расчет которых с вычислительной точки зрения довольно трудоемок. Для упрощения вычислений произведем расчет знаменателя отдельно в символьном виде и затем на заключительном шаге заменим символы соответствующими значениями.
Рассмотрим вектор дисконт-факторов
Получим символьный вектор интегралов
И затем подставим его в формулу (2.6):
|
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 371. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 . Обозначим плотность распределения условной вероятности превышений наблюдаемой
. Обозначим плотность распределения условной вероятности превышений наблюдаемой
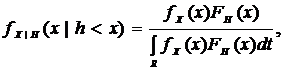 (2.3)
(2.3)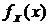 - плотность распределения случайной величины X ;
- плотность распределения случайной величины X ; - функция распределения вероятности случайной величины Н.
- функция распределения вероятности случайной величины Н.
 , то оно принадлежит области притяжения семейства распределений Фреше.
, то оно принадлежит области притяжения семейства распределений Фреше.
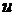 (
(  - зафиксированноеусловное превышение (
- зафиксированноеусловное превышение (  при
при 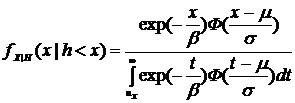 , (2.4)
, (2.4) , (2.5)
, (2.5) - первоначальный момент фиксирования убытков.
- первоначальный момент фиксирования убытков.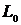 произошел в момент
произошел в момент  , и действующие однолетние ставки Libor, установленные с момента
, и действующие однолетние ставки Libor, установленные с момента 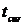 составляли
составляли 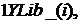
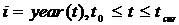 , тогда приведенная стоимость (PV) убытка
, тогда приведенная стоимость (PV) убытка 

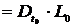


 выражений 2.4, 2.5 , реализованного в пакете MATLAB.
выражений 2.4, 2.5 , реализованного в пакете MATLAB.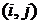 рассмотрим вектор данных вида
рассмотрим вектор данных вида  , где
, где 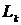 - величина убытка категории
- величина убытка категории  и превышающего начальный порог
и превышающего начальный порог 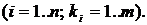
 , где
, где  - дисконт-фактор;
- дисконт-фактор; - условные превышения.
- условные превышения.
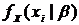 и
и 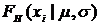 соответствующими распределениями:
соответствующими распределениями: (2.6)
(2.6)
 , не зависит от величины начального порога и
, не зависит от величины начального порога и  .
. :
: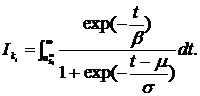
 (2.7)
(2.7)