Стохастическая модель Монте-Карло аппроксимации случайной суммы

Рассмотрим совокупную величину агрегированных убытков AggLoss,

произошедших за один год:

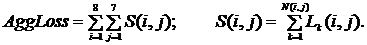
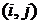Предполагается, что по каждой категории риска  величины убытков  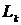распределены одинаково  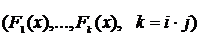и попарно независимы для различных категорий 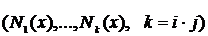. Частоты убытков распределены одинаково  и имеют структуру зависимости, определяемую параметрами  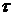или RankCorr.

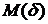Пусть  число итераций, требуемых для сходимости стохастического процесса, с точностью 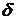. Критерию выбора числа итераций и исследованию сходимости и устойчивости реализованной стохастической модели посвящен раздел 3.3 настоящего исследования.

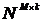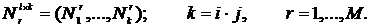
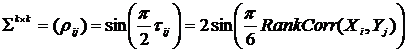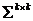На первом этапе необходимо смоделировать М коррелированных векторов  случайных частот наступления убытков (frequency) с параметрами или RankCorr:

1. Приведем корреляцию Кендалла или Спирмена к линейной корреляции Пирсона для рассматриваемых к случайных процессов:

;

2. При помощи копулы С для корреляционной матрицы  сгенерируем М векторов  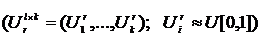равномерно распределенных случайных величин с корреляционными параметрами  или RankCorr.

Использованы следующие функции пакета MATLAB:

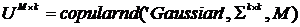 - Гауссова копула.

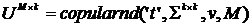 - t-копула Стьюдента с v-степенями свободы.

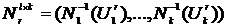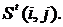
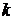3. Выполним обратное преобразование  и получим искомый набор зависимых векторов частот с заранее заданными параметрами корреляции  или RankCorr .

На втором этапе для каждой категории риска  на каждой смоделированной траектории частот возникновения убытков t необходимо получить распределение случайной суммы убытков

1. Проведем дискретизацию распределений величин убытков  методом взвешенного среднего, получим  векторов вида: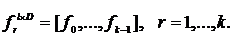 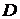- число точек дискретизации.

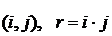Рассмотрим t - шаг моделирования и категорию риска . Вектор частот убытков на t - шаге равен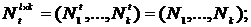 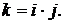 Распределение совокупной величины убытка  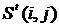по категории риска  равно: .

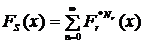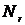2. Воспользуемся быстрым преобразованием Фурье для оценки свертки  функций распределений .

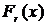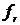· Применим FFT (быстрое преобразование Фурье) к вектору  - дискретизации функции распределения : .

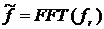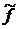· Возведем вектор  в степень : .

· Применим обратное преобразование Фурье к вектору  : .

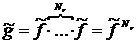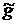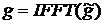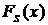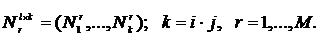
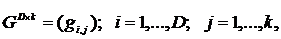В соответствие с результатами, полученными ранее, вектор g задает искомое дискретное распределение случайной суммы  для категории риска  и количества произошедших событий  (на t-траектории).

3. Выполним п. 2 для каждой категории  и для всех точек траектории частот:

В результате выполнения п.З будут получены М векторов размерности [Dxk]:

 задающих дискретное распределение случайных сумм  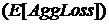для каждой точки траектории частот наступления убытков. Полученный набор векторов использован для расчета ожидаемой величины совокупного агрегированного убытка  объема риска (показателей - VaR, ES) и величины рискового капитала (CaR).