
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Интегральная формула Муавра-Лапласа. Вероятность отклонения относительной частоты случайного события от его вероятности в каждом отдельном испытании.Стр 1 из 15Следующая ⇒ Вероятности гипотез. Формула Бейеса. P(A)=P(A|B₁)*P(B₁)+ P(A|B₂)*P(B₂)+…+ P(A|Bn)*P(Bn)- формула полной вероятности. Событие А может наступить при условии появления одного из нескольких событий B₁,B₂,…,Bn, образующих полную группу. Тка как, заранее не известно, какое из B₁,B₂,…,Bn произошло, их называют гиполтезами. Пусть произведено испытание, в результате которого событие А произошло. Требуется найти вероятности гипотез B₁,B₂,…,Bn при условии, что А произошло, т.е. найти P(B₁|A), P(B₂|A),…, P(Bn|A); P(ABk)= P(A)*P(Bk|A)=P(Bk)*P(A|Bk),k=1,2,3,…,n P(Bk|A)=P(Bk)*P(A|Bk)/P(A) По формуле полной вероятности P(A) находим:P(Bk|A)=P(Bk)*P(A|Bk)/ Эти формулы называются формулами Бейеса. Они позволяют перераспределить вероятности гипотез B₁,B₂,…,Bn, если известно, что произошло событие А. Последовательность неизвестных испытаний. Формула Бернулли. Пусть проводится серия независимых испытаний, в каждом из которых некоторое событие А может произойти с вероятностью р или не произойти с вероятностью q=1-р. Если серия состоит из n испытаний, то вероятность того, что событие А произошло m раз (не важно каких испытаний), равна Pn(m)= Локальная формула Муавра-Лапласа. Формула Пуассона. Для больших значений n пользоваться формулой Бернулли неудобно, т.к. требуется вычислить n!(эн факториал). В этом случае применяют асимптотическую формулу Муавра-Лапласа(локальную): Pn(m) Формула дает хорошее приближение при больших значениях n (чем больше, тем лучше). Однако этой формулой пользуются, когда параметр λ=np  Имеются таблицы для значения функции φ(x)=(1/ φ(-x)= φ(x)- если функция четная. Если λ=np<=10, то используют формулу Пуассона: Pn(m) Интегральная формула Муавра-Лапласа. Вероятность отклонения относительной частоты случайного события от его вероятности в каждом отдельном испытании. Если требуется найти вероятность того, что событие А произойдет от m₁ до m₂ раз (m₁<m₂) в серии из n испытаний, то применяют интегральную формулу Муавра-Лапласа( для больших значений): Pn(m₁ Таблицы составлены для x>0, для x<0 применяют свойство Ф(-x)= -Ф(x). Pn(m₁ Интегральная формула Муавра-Лапласа может быть применена для вычисления вероятностей отклонения относительной частоты наступления события А от его вероятностей р не более, чем на заданную величину Это неравенство можем записать в развернутом виде: - Неравенство будет выполнено , если в серии из n независимых испытаний, данное событие А произойдет от m₁ раз равное n(p- Интегральная формула Муавра-Лапласа дает нам вероятность Рn(l m/n-p l Таким образом, вероятность выполнения такого неравенства равна Рn(l m/n-p l Из данной формулы можно получить закон больших чисел, заключающейся в том, что какого бы не было мало
13 Определение и основные виды случайных величин. Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены. Пример1. Число родившихся мальчиков среди ста новорожденных есть случайная величина, которая имеет следующие возможные значения: 0,1,2,…,100. Пример2. Расстояние, которое пролетит снаряд при выстреле из орудия, есть случайная величина. Действительно, расстояние зависит не только от установки прицела, но и от многих других причин (силы и направление ветра, температура и т.д.), которые не могут быть полностью учтены. Возможные значения этой величины принадлежат некоторому промежутку (a, b). Мы будем далее обозначать случайные величины прописными буквами X, Y, Z, а их возможные значения соответствующими строчными буквами x, y, z. Например, если случайная величина Х имеет три возможных значений, то они будут обозначены так: х1, х2, х3.
14.Биноминальный закон распределения дискретной случайной величины. Примеры. Дискретной (прерывной) величиной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным. Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически. Так как в одном испытании случайная величина принимает одно и только одно возможное значение, то события X=x1, X=x2, …, X=xnобразуют полную группу; следовательно, сумма вероятностей второй строки таблицы равна единице: p1+p2+…+pn=1. Пример. В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 руб. и десять выигрышей по 1 руб. Найти закон распределения случайной величины X – стоимости возможного выигрыша для владельца одного лотерейного билета. Решение. Напишем возможные значения X: х1 =50, х2 =1, х3=0. Вероятности этих возможных значений таковы: p1 =0,01, p2=0,1, p3=1-( p1+ p2)0,89. Контроль: 0,01+0,1+0,89=1.
Закон распределения дискретной случайной величины можно изобразить и графически, для этого в прямоугольной системе координат строят точки (х1, p1), а затем соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения. Для того, чтобы найти закон распределения величины Х, надо определить возможные значения Х и их вероятности. Очевидно, событие А в n испытаниях может либо не появиться, либо появиться 1 раз, либо 2 раза, …, либо n раз. Таким образом, возможные значения Х таковы: х1 =0, х2 =1, х3=2, … хn+1 =n. Остается найти вероятности этих возможных значений, для чего достаточно воспользоваться формулой Бернулли:
Данная формула является аналитическим выражением искомого закона распределения. Закон назван биноминальным потому, что правую часть равенства (*) можно рассматривать как общий член разложения бинома Ньютона
Таким образом, первый член разложения pn определяет вероятность наступления рассматриваемого события n раз в n независимых испытаниях; второй член npn-1q определяет вероятность наступления события n-1 раз; …; последний член qnопределяет вероятность того, что событие не повится ни разу. Пример. Монета брошена 2 раза. Написать в виде таблицы закон распределения случайной величины X – числа выпадений герба. Решение. Вероятность появления герба в каждом бросании монеты При двух бросаниях монеты герб может появиться либо 2 раза, либо 1 раз, либо совсем не появиться. Таким образом, возможные значения X таковы: Найдем вероятности этих возможных значений по формуле Бернулли:
Напишем искомый закон распределения:
Контроль: 0,25+0,5+0,25=1.
15. Распределение Пуассона. Примеры.
Пусть производится n независимых испытаний, в каждом из которых вероятность появления событияА равна p. Для определения вероятности k появлений события в этих испытаниях используют формулу Бернулли. Если же n велико, то пользуются асимптотической формулой Лапласа. Однако, эта формула непригодна, если вероятность события мала (p ≤0,1). В этих случаях (n велико, p мало) прибегают к асимптотической формуле Пуассона. Требуется найти вероятность того, что при очень большом числе испытаний, в каждом из которых очень большом числе испытаний, в каждом из которых вероятность события очень мала, событие наступит ровно k раз. Допустим, произведение np сохраняет постоянное значение, а именно np = λ. Это означает, что среднее число появлений события в различных сериях испытаний, при различных значениях n, остается неизменным. Воспользуемся формулой Бернулли для вычисления интересующей нас вероятности:
Так как
Приняв во внимание, что n имеет очень большое значение, вместо
Итак (для простоты записи знак приближенного равенства опущен),
Эта формула выражает закон распределения Пуассона вероятностей массовых (n велико) редких (p мало) событий. Пример. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,0002. Найти вероятность того, что на базу прибудут 3 негодных изделия. Решение. По условию n =5000, p =0,0002, k =3. Найдем λ: λ= np=5000·0,0002=1. Искомая вероятность по формуле Пуассона приближенно равна
16. Геометрическое распределение дискретной случайной величины. Примеры. Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы). Закон распределения дискретной случайной величины можно изобразить и графически, для этого в прямоугольной системе координат строят точки (х1, p1), а затем соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения. Так как в одном испытании случайная величина принимает одно и только одно возможное значение, то события X=x1, X=x2, …, X=xnобразуют полную группу; следовательно, сумма вероятностей второй строки таблицы равна единице: p1+p2+…+pn=1.
17. Мат ожиданием (МО) дискретной случайной величины (СВ) называют сумму произведений всех ее возможных значений на их вероятности. Пусть СВ х может принимать только значения Х1, Х2,…,Хn, вероятность которых соответственно равны Р1, Р2,…,Рn. Тогда МО М(Х) св Х определяется равенство: М(Х)=Х1Р1+Х2Р2+…+ХnРn. Вероятностный смысл МО: МО приблизительно равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений СВ Свойства МО: 1 МО постоянной величины равно самой постоянной М(С)=С; 2 Постоянный множитель можно выносить за знак МО: М(СХ)=С*М(Х) 3 МО произведения двух независ. СВ равно произведению их МО: М(XУ)=М(Х)*М(У) 4 МО суммы двух СВ равно сумме МО: М(Х+У)=М(Х)+М(У)
18.Дисперсией (рассеянием) дискретной случайной величины (СВ) называют мат. ожидание (МО) квадрата отклонения СВ от ее МО: D(X)=M[X-M(X)]2. Для того, чтобы найти дисперсию, достаточно вычислить сумму произведений возможных значений квадрата отклонения на их вероятности. Обозначают: D(X)= Свойства дисперсии случайной величины: 1. Дисперсия постоянной величины С равно нулю: D(C)=0; 2.Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: D(CX)=C2D(X). 3.Дисперсия двух независимых величин равна сумме дисперсий этих величин: D(X+Y)=D(X)+D(Y) 4.Дисперсия разности двух независимых величин Х и У равна сумме двух дисперсий: D(X-Y)=D(X)+D(Y). Дисперсия имеет размерность квадрата случайной величины. В тех случаях, когда нужно иметь числовую характеристику рассеяния возможных значений в той же размерности, что и сама случайная величина используют среднее квадратическое отклонение. Средним квадратическим отклонением случайной величины называют корень квадратный из ее дисперсии:
19.Дисперсия числа появлений события А в n независимых испытаниях, в каждом из которых вероятность р появлений события постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании: D(X)=npq. Среднее квадратическое отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин: Мат. ожидание M(x) числа наступлений некоторого события А в серии из n независимых испытаний равно: М(х)=np, где р – вероятность наступления события А в каждом отдельном испытании.
20. Начальным моментом порядка k случайной величины Х называют мат ожидание величины Хk: νk=М(Хk). Центральным моментом порядка k случайной величины Х называют мат ожидание величины (Х-М(Х))k: μk=М[(Х-М(Х))k] Легко выводятся соотношения, связывающие начальные и центральные μ2=ν2-ν12 Нетрудно, исходя из определения центрального момента и пользуясь свойствами мат ожидания, получить формулы: μ3=ν3-3ν1ν2+2ν13 μ4=ν4-4ν3ν1+6ν2ν12-3ν14.
21.Неравенство Чебышева.
D(X)=(x1-M(X))2*p1+(x2-M(X))2*p2+…+(xn-M(X))2*pn Все слагаемые в этой сумме неотрицательные.Отбросим из них те, у которых из них модуль
22. Теория Чебышева.Пусть х1,х2…хn попарно независимые величины с равномерно ограниченными дисперсиями, т.е. D(xi)
Практическое применение. Пусть некоторую величину измеряют в одинаковых условиях. Будем полагать,что:1)измерения независимы друг от друга 2)приборы не делают систематических ошибок 3)приборы обеспечивают опред. точность измерении. При выполнении этих условии мы можем применить т.Чебышева к показаниям приборов как к случайным величинам.х1,х2…хn при достаточном большом n вероятность выполнения неравенства
23.Пусть в серии из n независимых испытании вероятность появления события Апостоянна и равна р. Тогда для всех
24.Ф-цией распределении случайной величины Х называют F(x)=P(X<x), равная вероятности того, что Х примет значение, меньше заданного числа (х-все числа). Св-ва: 1)Область определения-все числа, область значения-[0;1] 2)F(x)-неубывающая ф-ция 3) (тут заканчивается фигурная скобка) р1+р2+…+рn,если хn<х Для непрерыв. случайной величины вероятность принятия какого-либо конкретного значения бесконечно мала. Поэтому имеет смысл говорить о вероятности попадания в некоторыйинтервал (а;b). Вероятность того, что Х попадет в этот интервал равнаP(X=(a;b))=F(b)-F(a)
25..Непрерывная случайная величина.Плотность распределения вероятностей,ее основные св-ва и вероятностный смысл. Для непрерывной СВ ф-ция распространения явл. непрерывной.Для непрерывной СВ вероятность принятия какого-либо конкретного значения бесконечно мала.Поэтому,имеет смысл говорить о вероятности попадания в некоторый интервал.Плотностью распространения вероятностей непрерывной СВ Х назыв. 1-ая производная от ее ф-ции распределения f(x)=F’(x),т.е.Fявл. первообразной для плотности распределения f. Св-ва плотности вероятности:1)f(x)>=0,для всех х,принадлежащих R;2)интеграл f(x)dx=1-условие плотности вероятности.
26.Числовые характеристики непрерывных СВ(мат.ожидание,дисперсия,среднеквадратическое отклонение,начальные и центральные моменты) Мат.ожидание непрерывной СВ Х,определ.поформуле:M(x)=интеграл х*f(x)dx Дисперсия:D(x)=byntuhfk(x-M(x))2F(x)dx Среднее квадратическое отклонение:Σ(x)=D(x) Начальный момент каждого порядка:Vk=интеграл от x2f(x)dx Центральный момент каждого порядка:µk=интеграл от (х-М(х))2*f(x)dx
27.Нормальное распределение непрерывной СВ и его числовые хар-ки.Формулировкацентральной предельной теоремы Ляпунова. Плотность вероятности нормального распределения имеет вид: f(x)=1/σ2п*exp(-(x-a)2/2σ2), σ,a=const.
28.Оценка отклонения теоретического распределения от нормального.Правило «3 сигм».Асимметрия и эксцесс. Правило «3 сигм»:Если случайная величина распределена нормально,то абсолютная величина ее отклонения от мат.ожидания не превосходит утроенной σ. На практике поступают так: Если распределение изучаемой СВ неизвестно,то правило «3 сигм» выполнено,то есть все основания считать,что изучаемые СВ распределенынормально.В противном случае-не нормально.
29. Показательным(экспоненц-ным) назыв. Распределение вероятностей непрерывн. СВ, заданное формулой:
Момент времени наступления некот. События в простом потоке событий, т.е. непрер. СВ с показат. Распределением. M(x)=∫ от 0 до + ∞ (xde^–λx)dx = 1/λ D(x)=∫ от 0 до + ∞ ((1-1/x)^2 * λe^–dx)dx=1/ λ^2 δ(x)=корень из D(x)=1/ λ Назовем элемент устройством. Элем нач. работать в момент врем. T0, а по истеч. врем. Длит-тьюt происходит поломка. F(t)=P(T<t) вер-ть безотказной работы за время t=P(t)=p(T>=t)=1-F(t) – ф-ция надежности.
30. Если каждому возможному значению случайной величины Х соответствует одно возможное значение случайной величины Y,то Y называют функцией случайного аргумента. Пусть Y = ф(X) – функция случайного аргумента Х, и требуется найти ее математическое ожидание, зная закон распределения Х. Если Х – дискретная случайная величина, то Если Х – непрерывная случайная величина, то M(Y) можно искать по-разному. Если известна плотность распределения g(y), то Если же g(y) найти сложно, то можно использовать известную плотность распределения f(x):
31.
Пусть
имеет распределение хи-квадрат с n степенями свободы. Распределение фишера-снедекора - непрерывное сосредоточенное на 32. Двухмерная функция распределения двухмерной случайной величины (Х, Y) равна вероятности совместного выполнения двух событий {Х <х} и {Y <у}: F(x,y)=p({X<x}⋅{Y<y}). Закон распределения дискретной двумерной СВ наз. Соответствие возможных знач. Этой СВ и их вер-ти. Свойства двухмерной плотности: 1 2 3 4
5
33.Рассмотрим прямоугольник ABCD со сторонами, параллельными координатным осям. Пусть уравнения сторон таковы: Х=х1, Х=х2, У=у1 и У=у2. Найдем вероятность попадания случайной точки (Х, У) в этот прямоугольник. Искомую вероятность можно найти, например, так: из вероятности попадания случайной точки в полуполосу АВ с вертикальной штриховкой (эта вероятность равна F(x2, y2)-F(x1, y2) вычесть вероятность попадания точки в полуполосуCD с горизонтальной штриховкой (эта вероятность равна F(x2, y1)-F(x1, y1):Р(х1<X<x2, y1<Y<y2)=[F(x2, y2)-F(x1, y2)]-[F(x2, y1)-F(x1, y1)]
34. Непрерывную двумерную величину можно задать, пользуясь дифференциальной функцией распределения. Здесь и далее мы будем предполагать, что интегральная функция всюду непрерывна и имеет всюду непрерывную смешанную частную производную второго порядка. Дифференциальной функцией распределения f(x, y) двумерной непрерывной случайной величины (Х, У) называют вторую смешанную частную производную от интегральной функции: f(x, y)=( δ2 F(x, y))/( δx δy). Геометрически эту функцию можно истолковать как поверхность, которую называют поверхностью распределения.
35. Плотностью совместного распределения вероятностей двумерной СВ (Х,У) называют смешанную производную второго порядка от функций распределения F(х,у). f(х,у)=∂2 F(х,у)/∂х∂у. Функция распределения F(х,у)=∫∫ f(x,у) dxdy. Вероятностный смысл плотности вероятности: P( х<x<+∆x; у<Y<y+∆y)≈f (x,у)*∆х∆у.
36. Пусть (Х,У) дискретная двумерная случайная величина с возможными значениями : (хiyi); i=1, 2,…к, j=1,2,…L. Вероятность того, что Х=хi при условии У=уjобозначим через Р(хi|yi), i=1,2,…К, j=1,2,…, L. Условное распределение величины Х при условии, что У=yj, называется совок-ть условных вероятностей: Р(х1|yi), Р(х2|yi)…Р(хi|yi).Условная вероятность вычисляется по формуле Р(хi|yi)= Р(хi|yi)/ Р(yi). Аналогично определяется распределение величины У при условии, что Х=Хi.
|
||||||||||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 382. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
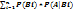
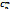 *
* 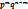 ,где
,где 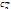 – число сочетаний, равное
– число сочетаний, равное  (1/
(1/ 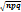 )*1/
)*1/ 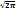 *
* 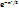 , гдеx=(m-np)/
, гдеx=(m-np)/ 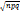 (p не равно 0 и 1); (1/
(p не равно 0 и 1); (1/  *
* 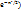 =φ(x).
=φ(x). 10.
10.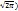 *
* 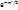 . Таблицы составлены для x>0.
. Таблицы составлены для x>0.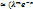 )/m!
)/m! m
m 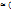 1/
1/  x, гдепределы интегрирования равны x₁=(m₁-np)/
x, гдепределы интегрирования равны x₁=(m₁-np)/ 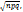 x₂=(m₂-np)/
x₂=(m₂-np)/ 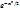 dx не выражается через элементарные функции, то используют специальные таблицы для функции Ф(x)=
dx не выражается через элементарные функции, то используют специальные таблицы для функции Ф(x)=  1/
1/ 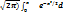 x.
x. . Другими словами требуется вероятность выполнения неравенстваl m/n-p l
. Другими словами требуется вероятность выполнения неравенстваl m/n-p l 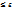 .
. m/n-p
m/n-p 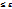 ; n(p-
; n(p-  )
) 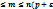 ).
).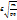 .
. )-Ф
)-Ф 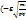 ) = 2Ф
) = 2Ф  .
. +∞ аргумент
+∞ аргумент 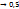 .
. , где k=0, 1, 2, …, n. (*)
, где k=0, 1, 2, …, n. (*)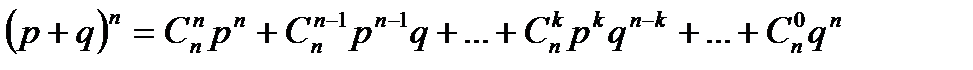 .
.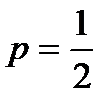 , следовательно, вероятность непоявления герба
, следовательно, вероятность непоявления герба 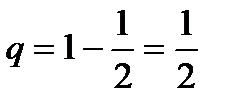 .
.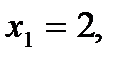
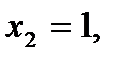

 .
.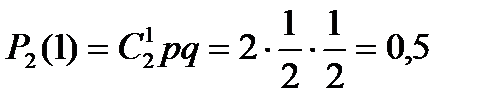 .
. .
. .
.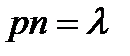 , то
, то 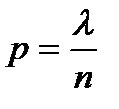 . Следовательно,
. Следовательно,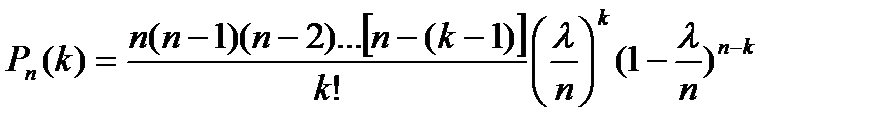 .
. найдем
найдем 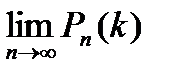 . При этом будет найдено лишь приближенное значение отыскиваемой вероятности: n хотя и велико, но конечно, а при отыскивании предела мы устремим n к бесконечности. Итак,
. При этом будет найдено лишь приближенное значение отыскиваемой вероятности: n хотя и велико, но конечно, а при отыскивании предела мы устремим n к бесконечности. Итак,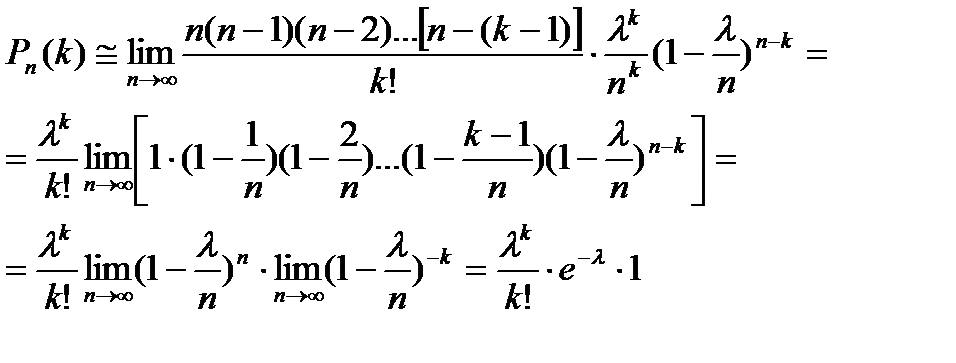
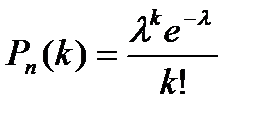 .
.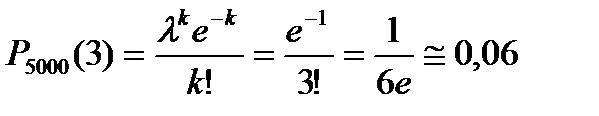 .
. (X)=
(X)= 


 для всех
для всех  >0.Доказательство.
>0.Доказательство. )
) .Для оставшихся хар-но неравенство
.Для оставшихся хар-но неравенство  . После чего сумма может только уменьшаться, тогда D(X) (xi1-M(X))2*pi1+(xi2-M(X))2*pi2+(xi3-M(X))2*pi3,где i1,i2,i3 номера оставшихся слагаемых, для которых хар-но неравенство
. После чего сумма может только уменьшаться, тогда D(X) (xi1-M(X))2*pi1+(xi2-M(X))2*pi2+(xi3-M(X))2*pi3,где i1,i2,i3 номера оставшихся слагаемых, для которых хар-но неравенство .Для остальных слагаемых D(X)
.Для остальных слагаемых D(X)  …
… 
 2(pi1+pi2+…+pi3). Здесь pi1+pi2+…+pi3=
2(pi1+pi2+…+pi3). Здесь pi1+pi2+…+pi3=  - это вероятность того,что х примет знач. такое, чтобы
- это вероятность того,что х примет знач. такое, чтобы

 Dmax. Тогда для произвольного
Dmax. Тогда для произвольного  > 0 вероятность выполнения неравенства
> 0 вероятность выполнения неравенства будет сколь угодна близка к 1 при достаточно большом кол-ве n.
будет сколь угодна близка к 1 при достаточно большом кол-ве n. сколь угодна близка к 1,т.е. почти достоверно можно сказать, что ср. арифмет. показания приборов не более чем на
сколь угодна близка к 1,т.е. почти достоверно можно сказать, что ср. арифмет. показания приборов не более чем на  отлич. от а.
отлич. от а. >0:
>0:  .Х1-случайная величина равная числу появлении события А в i-том испытании.Ясно,что Хi=0 или 1. М(Х1)=1*р+0*q=р, i=1,2,3…n. Применим к случайным величинам Х1,Х2…Хnт.Чебышева.
.Х1-случайная величина равная числу появлении события А в i-том испытании.Ясно,что Хi=0 или 1. М(Х1)=1*р+0*q=р, i=1,2,3…n. Применим к случайным величинам Х1,Х2…Хnт.Чебышева. . Учитывая,что Х1+Х2+…+Хn=m(кол-во раз произошедших испытании) М(Х1)=М(Х2)=…=М(Хn)=р
. Учитывая,что Х1+Х2+…+Хn=m(кол-во раз произошедших испытании) М(Х1)=М(Х2)=…=М(Хn)=р
 ;
;  4)для дискретной случайной величины график ф-ции имеет вид: F(x)(тут нач. фигурная скобка) 0,если х
4)для дискретной случайной величины график ф-ции имеет вид: F(x)(тут нач. фигурная скобка) 0,если х  х1 р1,еслих1<х
х1 р1,еслих1<х  х2 р1+р2,если х2<х
х2 р1+р2,если х2<х 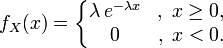 λ>0 const
λ>0 const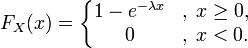 - Ф-ция показательного распределения
- Ф-ция показательного распределения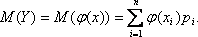
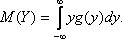
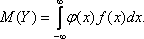
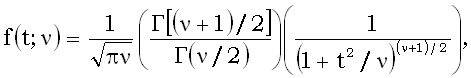 Распределение вероятностей непрерывной случайной величины, плотность вероятности которого задается этой формулой наз. Распределением Стьюдента.
Распределение вероятностей непрерывной случайной величины, плотность вероятности которого задается этой формулой наз. Распределением Стьюдента. — совместно независимые стандартные нормальные случайные величины, то есть:
— совместно независимые стандартные нормальные случайные величины, то есть: 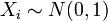 . Тогда случайная величина
. Тогда случайная величина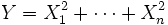
 распределение вероятностей с плотностью
распределение вероятностей с плотностью 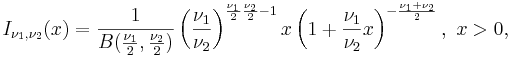 .
.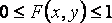
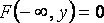 ,
, 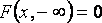
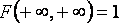
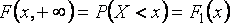
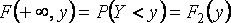
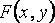 неубывающая функция по каждому из своих аргументов при фиксированном другом аргументе.
неубывающая функция по каждому из своих аргументов при фиксированном другом аргументе.