
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Использование многочленов для построения конечных полей⇐ ПредыдущаяСтр 16 из 16 Зафиксируем любое кольцо Rс единицей е и рассмотрим множество Mrвыражений вида а0 + a1x1+ а2х2 + ... + апхп, где a0, a1,..., ап ÎR. Выражение вида а0 + a1x1+ а2х2 + ... + апхп называется многочленомот x над кольцом Rи обозначается в виде а(х). Множество всех многочленов от x над кольцом Rобозначается через R[x]. Многочлены а(х), b(х) над полем Р наазывалются сравнимыми по многочлену Для сравнений многочленов имеют место все свойства для сравнения целых чисел по модулю, сравнения многочленов можно почленно складывать, вычитать и умножать. Отношение сравнимости по многочлену
Теорема 1. Множество Теорема 2. Кольцо На кольцо классов
Таким образом, каждому классу сопоставлен многочлен вида  Из представления элементов кольца В частности, если в качестве Р взять знакомое нам поле вычетов Z/p по простому модулю р, а в качестве Пример. Построить поле Галуа GF(8). Так как 8 = 23, то в качестве исходного поля Р можно взять GF(2) = {0, е}, а в качестве
Тогда элементами исходного поля можно считать многочлены:
|
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 227. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
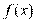 , если они при делении на
, если они при делении на 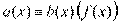 .
.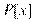 , и потому последнее разбивается на попарно непересекающиеся классы. В одном классе содержатся все многочлены, дающие при делении на
, и потому последнее разбивается на попарно непересекающиеся классы. В одном классе содержатся все многочлены, дающие при делении на  , обозначим в виде
, обозначим в виде  , а множество всех классов — через
, а множество всех классов — через  . На множестве
. На множестве 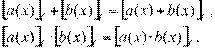
 .
. , то выбранный остаток имеет вид
, то выбранный остаток имеет вид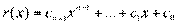 .
. , причем разным классам сопоставлены разные такие многочлены), и все такие многочлены оказались занятыми. Иначе говоря, между множествами классов и многочленов вида
, причем разным классам сопоставлены разные такие многочлены), и все такие многочлены оказались занятыми. Иначе говоря, между множествами классов и многочленов вида  установлено взаимно однозначное соответствие, и потому вместо классов можно оперировать многочленами вида указанного вида. При этом операциям + и × над классами будут соответствовать операции Å и Ä над соответствующими многочленами. Для нахождения результатов операций Å и Ä над многочленами вида
установлено взаимно однозначное соответствие, и потому вместо классов можно оперировать многочленами вида указанного вида. При этом операциям + и × над классами будут соответствовать операции Å и Ä над соответствующими многочленами. Для нахождения результатов операций Å и Ä над многочленами вида  .
.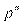 элементов. Это поле называют полем Галуаиз
элементов. Это поле называют полем Галуаиз  элементов и обозначают в виде GF(pn). Отметим без доказательства, что любые два поля порядка рп изоморфны и полями вида GF(pn) исчерпываются с точностью до изоморфизма все конечные поля.
элементов и обозначают в виде GF(pn). Отметим без доказательства, что любые два поля порядка рп изоморфны и полями вида GF(pn) исчерпываются с точностью до изоморфизма все конечные поля. .
. .
.