
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Алгоритм Евклида для многочленовАлгоритм Евклида - это правило нахождения наибольшего общего делителя для многочленов а(х) и b(х) (над полем Р) при b(х) ≠ 0, заключающееся в следующем. Многочлен а(х) делят с остатком на b(х). Если полученный остатокr1(x)неравен нулю, то b(х) делят на полученный остаток r1(x), затем r1(x) делятна остаток r2(х) от деления b(х) на r1(x), и так далее, пока не получат остаток, равный нулю: а(x) = b(х)q1(х) + r1(х), b(х) = r1(x)q2(x) + r2(x), r1(x) = r2(x)q3(x) + r3(x), rn-1(x) = rn(x)qn+1(x), гдеdeg b(x) > deg r1(x) > deg r2(x) > ... >degrn(x) и rn(x) — последний отличный от нуля остаток. Так как степени остатков строго убывают, то процесс этот всегда конечен. Из приведенных выше соотношений следуют два утверждения: 1) Последний отличный от нуля остатокrп(х) в алгоритме Евклида, примененном к многочленам а(х) и b(х) ¹ 0 из кольца Р[х], является наибольшим общим делителем многочленов a(х), b(х). 2) Многочлен d(x) из кольца Р[х]является наибольшим общим делителем многочленов а(х), b(х) в том и только в том случае, когдаd(x) = crn(х), где сÎР и с ¹ 0. Многочлены a1(x), a2(x), ..., an(x) называются взаимно простыми, если их наибольший общий делитель равен единице, (a1(x), a2(x) ,... , an(x)) = 1. Для любых многочленов а(х), b(х), с(х) имеют место утверждения: 1)(а(х),b(х)) = 1Û существуют u(x), v(x) ÎP[х]: a(xu(x)+ b(x)v(x) = 1. 2)(а(х),b(х)) = 1, (а(х),с(х)) = 1 Þ (а(х), b(х)с(х)) = 1. 3)(a(x),b(x))=d(x)¹ 0Þ 5) а(х)|с(х), b(х)|с(х) и (a(х),b(х)) = 1 Þ a(х)b(х)|с(х). 6)(a(х),b(х)) = 1 иa1(x)|a(x), b1(x)|b(x), Þ (a1(x), b1(x)) = 1. 7)(а(х), b(х)) = 1 и m, n- любые натуральные числа Þ(а(х)m,b(х)n) = 1.
Разложение многочлена в произведение неприводимых многочленов Многочлен а(х) из Р[х]степени n> 0 называется неприводимымнад полем Р, если не существует многочленов а1(х),a2(х) Î Р[х]таких, что: а(х)=а1(х)а2(х), 0<degai(х) <п, i = 1,2. В противном случае многочлен а(х) называется приводимымнад Р. Многочлены нулевой степени и нулевой многочлен не относятся ни к приводимым, ни к неприводимым многочленам.  Любой многочлен а(х) степени n> 0 над полем Р разлагается в произведение неприводимых над полем Р многочленов, и такое разложение единственно с точностью до перестановки сомножителей и их отличий на множители нулевой степени. Любой многочлен а(х) степени п>0 над полем Р может быть представлен в следующем виде:
Такое представление многочлена а(х) называется его каноническим разложениемнад полем Р. Оно единственно с точностью до перестановки сомножителей вида Каноническое разложение многочлена на неприводимые множители существенно зависит от того поля, над которым этот многочлен рассматривается. Корни многочлена Пусть f(х) = anxn + an-1xn-1 + ... + a1x + а0— многочлен над кольцом R и r- некоторый элемент кольца R. Значение произведения двух многочленов при х=r равно произведению их значений при том же значении х=r только если r перестановочен со всеми коэффициентами многочлена f2(x). В частности, это свойство имеет место для любых многочленов над коммутативным кольцом, а значит, и над любым полем. Элемент r кольца Rназывается корнеммногочлена f(x)ÎR[x], если значение многочлена f(x) при x=r равно нулю, то есть f(r)= 0. Теорема Безу В этом разделе будем рассматривать многочлены над некоторым полем Р. Сформулируем теорему Безу: Значение многочленаf(x) над полем Р при х = а равно остатку от деления многочлена f(x) на многочлен x – a. Элемент а поля Р является корнем многочленаf(x)ÎP[x]тогда и только тогда, когдаf(x) делится на многочлен х – а. Отсюда, в свою очередь, можно заключить, что многочленf(x) степени п над полем Р может иметь в поле Р не более п различных корней. У многочленов над кольцами количество корней может превышать степень самого многочлена. Основная теорема алгебры Любой многочлен над полем комплексных чисел К имеет в К хотя бы один корень. Любой многочлен степени n> 1 из кольца многочленов над полем комплексных чисел K[x] разлагается над K в произведение многочленов первой степени (линейных множителей). Если многочленf(x) над полем действительных чиселR имеет комплексный корень α = а + bi, то корнемf(x) является и сопряженное к α числонад полем К: Любой многочлен нечетной степени над полем действительных чисел R имеет по крайней мере один действительный корень. Так как рассматриваемый над полем комплексных чисел этот многочлен имеет нечетное число корней, а все комплексные корни являются парами со своими сопряженными. Неприводимыми над полем R являются лишь многочлены первой степени вида (x – a) и многочлены второй степени вида ах2+ bх + с с отрицательными дискриминантами (для которых выполняется условие b2 – 4ас < 0). |
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 484. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
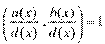 .
. , где cÎP, p1(x), ... ,pr(x) — различные унитарные и неприводимые над Р многочлены,k1,.., krÎN.
, где cÎP, p1(x), ... ,pr(x) — различные унитарные и неприводимые над Р многочлены,k1,.., krÎN. iÎ{1, 2,...,r}.
iÎ{1, 2,...,r}. = a – bi. (Сопряженные комплексные числа отличаются знаками своих мнимых частей.)
= a – bi. (Сопряженные комплексные числа отличаются знаками своих мнимых частей.)