
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Статистична обробка нафтогазової інформаціїВипадкова величина (ВВ) – величина, яка в результаті досліду може набути того чи іншого значення, причому заздалегідь невідомо якого саме. Математичне очікування – середнє арифметичне. Математичне очікування для дискретних і неперервних випадкових величин (ВВ) визначають за формулою (4.1):
де Рі – імовірність значення хі; хі – можливі величини х; Мода –число, яке найбільш часто зустрічається в даній множині чисел. Модою дискретної ВВ називають її найімовірніше значення, а неперервної – те її значення, якому відповідає максимальна щільність розподілу. Медіана – число, яке є серединою множини чисел: половина чисел мають значення більші, ніж медіана, а половина чисел – менші. Медіаною ВВ називають таке її значення, для якого однаково імовірне виявлення значень ВВ, більших або менших, ніж це значення Р(X<Me)=Р(X>Me). Дисперсія – середнє значення квадратів відхилення елементів вибірки від вибіркового середнього, характеризує розкид вибіркових значень. Дисперсія ВВ – це математичне сподівання квадрата відхилення ВВ σ2 ( D= Геометрично дисперсію розглядають як центральний момент інерції площі, обмеженої кривою розподілу. Стандарт оцінює стандартне відхилення по вибірці. Це міра того, наскільки широко розкидані точки даних відносно їх середнього.
 Коефіцієнт варіації характеризує розкид значень ВВ:
Коефіцієнт асиметрії визначає скошеність розподілу ВВ, тобто оцінює відхилення розподілу від симетричного: А=
де Коефіцієнт ексцесу оцінює шпилястість (приплюснутість) розподілу ВВ: Е=
Закон розподілу випадкових величин – зв’язок між можливими значеннями випадкової величини та відповідними їм ймовірностями. Функція розподілу випадкових величин – імовірність того, що випадкова величина набуде значення, що не більше заданого. Кумулятива – графік в наступній системі координат: вісь абсцис – межі інтервалів, вісь ординат – накопичені відносні частоти. Щільність розподілу – функція відношення імовірності того, що випадкова величина Х набуде значення в нескінченно малому інтервалі х+Δх, до довжини цього інтервалу. Графічне зображення кривих розподілу з різними коефіцієнтами асиметрії та ексцесу зображено на рис. 4.1.
Рис. 4.1. Графічне зображення кривих розподілу
Завдання: для заданої вибірки (статистичного ряду) випадкових величин нафтогазових даних (наведено у табл. 4.1) визначити наступні статистичні параметри – максимальне і мінімальне значення, об’єм вибірки, оптимальну кількість інтервалів, величину інтервалу, розмах, математичне очікування, моду, медіану, дисперсію, стандарт, коефіцієнт варіації, асиметрію та ексцес. Провести групування випадкових величин, побудувати гістограму, полігон та кумулятиву. Методика виконання статистичної обробки із використанням програми MS Excel. 1. Проводимо сортування випадкових величин від мінімального хmin до максимального значення xmax. З цією метою рекомендується використати функцію «СОРТИРОВКА» програми MS Excel. 2. Визначаємо максимальне xmax і мінімальне хmin значення вибірки. З цією метою рекомендується використати функцію «МАКС» і «МИН» відповідно програми MS Excel. Визначаємо об’єм вибірки використовуючи функцію «СЧЁТ» програми MS Excel. Для даних прикладу N=100. 3. Визначаємо оптимальну кількість інтервалів за допомогою формули Стерджеса k=1+3,32·lgN. 4. Визначаємо розмах вибірки. Для даних прикладу R=xmax – xmin. 5. Визначаємо величину інтервалу l=R/k.
Таблиця 4.1 |
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 395. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 ;
;  , (4.1)
, (4.1) 2) від її центра
2) від її центра  і характеризує розкид її значень відносно математичного сподівання. Дисперсія для дискретних і неперервних ВВ визначається за формулами:
і характеризує розкид її значень відносно математичного сподівання. Дисперсія для дискретних і неперервних ВВ визначається за формулами: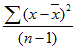
 ;
;  , (4.2)
, (4.2) ; (4.3)
; (4.3)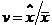 (4.4)
(4.4) А=µ3/σ3, (4.5)
А=µ3/σ3, (4.5)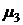 – центральний момент третього порядку.
– центральний момент третього порядку. Е=µ4/σ4–3, (4.6)
Е=µ4/σ4–3, (4.6)