Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Момент количества движения материальной точки и механической системы относительно центра.Рассмотрим две любые точки Внутренние силы действуют попарно, поэтому
Геометрическая сумма всех внутренних сил механической системы равна нулю.
Найдем сумму моментов сил Геометрическаясумма моментов всех внутренних сил механической системы относительно произвольно выбранного центра равна нулю. Теорема об изменении момента количества движения(кинетического момента) механической системы относительно неподвижного центра(неподвижной оси). Умножим каждое из уравнений слева векторно на радиус-вектор соответствующей точки и сложим все полученные уравнения: Учитывая второе основное свойство внутренних сил, получаем: Вектор Сумма моментов количеств движения всех точек механической системы называется моментом количества движения или кинетическим моментом механической системы относительно центра O;
Первое слагаемое в квадратной скобке равно нулю, так как векторно перемножаются два коллинеарных вектора. Таким образом,  Сравнивая последний результат с левой частью равенства (3.7), получаем: Доказана теорема об изменении кинетического момента механической системы: производная по времени от кинетического момента механической системы относительно произвольно выбранного неподвижного центра равна сумме моментов всех приложенных к системе внешних сил относительно того же центра. Теорема об изменении кинетического момента механической системы относительно её центра масс Пусть система отсчета Oxyz неподвижная (инерциальная). Система Можно показать (доказательство.......), теорема об изменении кинетического момента сохраняет свой вид, если в качестве моментной точки используется центр масс механической системы. Таким образом, производная по времени от кинетического момента механической системы относительно ее центра масс равна сумме моментов относительно центра масс всех приложенных к системе внешних сил. |
|||||
|
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 223. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
и 
механической системы, состоящей из n материальных точек. В соответствии с третьим законом Ньютона они взаимодействуют с силами, равными по модулю и действующими по одной прямой в противоположные стороны (Рис.3.1). При этом 
или 
(3.2) Таким образом:
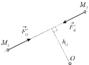
и 
относительно произвольно выбранной точки O. Как следует из определения, моменты этих сил противоположны по направлению и равны по модулю. Следовательно, их сумма равна нулю. Учитывая, что внутренние силы всегда действуют попарно, получаем второе основное свойство внутренних сил: 
(3.3) Таким образом:
(3.7)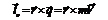
называется моментом количества движения материальной точки относительно центра O.
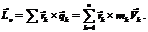(3.8)Вычислим производную по времени от кинетического момента:
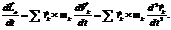
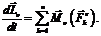(3.9)
движется поступательно по отношению к Oxyz, причем ее начало во все время движения совпадает с центром масс механической системы (Рис.3.2). Такая система координат называется системой Кенига. Следует заметить, что система Кенига играет исключительно важную роль при описании движения твердого тела.
(3.13)