
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Работа силы тяжести, работа упругой силы и работа вращающего момента (пары сил). Работа силы тяжести.При вычислении работы силы тяжести мы рассматриваем ограниченную область пространства вблизи поверхности Земли, размеры которой малы по сравнению с размерами Земли. Направим ось z вертикально вверх. Точка M с массой m перемещается по некоторой траектории из положения Вычислим работу силы тяжести:
Сила тяжести – потенциальная сила. Ее работа не зависит от траектории точки, а определяется перепадом высот Таким образом, Работа силы тяжести положительна, если точка теряет высоту (опускается) и отрицательна, если точка набирает высоту. Работа упругой силы. Понятие упругой силы обычно ассоциируется с реакцией линейно–упругой пружины. Направим ось x вдоль пружины в сторону ее растяжения. Под
Сила реакции пружины пропорциональна ее удлинению Вычислим мощность упругой силы:
Работа упругой силы при перемещении конца пружины из Как видно, упругая сила потенциальна. Потенциальная энергия тела Ьравна  Работа вращающего моментаПусть сила
32. Теорема об изменении кинетической энергии механической системы. Умножим каждое из дифференциальных уравнений движения точек механической системы скалярно на скорость соответствующей точки и сложим все полученные уравнения:
Учитывая определения кинетической энергии механической системы и мощности силы, получаем:
Доказана теорема об изменении кинетической энергии механической системы в дифференциальной форме: Производная по времени от кинетической энергии механической системы равна сумме мощностей всех приложенных к системе внешних и внутренних сил. |
||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 292. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 в положение
в положение  (Рис.5.2). Проекции силы тяжести на оси координат равны:
(Рис.5.2). Проекции силы тяжести на оси координат равны:  гдеg – ускорение свободного падения.
гдеg – ускорение свободного падения.

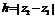 между начальным и конечным положениями точки, будучи равной убыли потенциальной энергии
между начальным и конечным положениями точки, будучи равной убыли потенциальной энергии  материального тела.
материального тела.
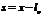 понимаем удлинение пружины (
понимаем удлинение пружины (  – длина нерастянутой пружины).
– длина нерастянутой пружины).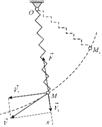
 гдеc – коэффициент жесткости пружины. Разложим вектор скорости точки M на две составляющие, одна из которых
гдеc – коэффициент жесткости пружины. Разложим вектор скорости точки M на две составляющие, одна из которых 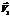 направлена вдоль пружины и определяет скорость ее растяжения, а вторая
направлена вдоль пружины и определяет скорость ее растяжения, а вторая  перпендикулярна пружине и определяет скорость точки M, полученную при повороте пружины без изменения ее длины (Рис. 5.3).
перпендикулярна пружине и определяет скорость точки M, полученную при повороте пружины без изменения ее длины (Рис. 5.3). т.к.
т.к. 
 в
в  оказывается равной
оказывается равной 
 . Заметим, что если поворачивать пружину вокруг шарнира O, не изменяя ее длины, то упругая сила не совершает работу.
. Заметим, что если поворачивать пружину вокруг шарнира O, не изменяя ее длины, то упругая сила не совершает работу. приложена в некоторой точке тела, имеющего ось вращения. Тело вращается с угловой скоростью
приложена в некоторой точке тела, имеющего ось вращения. Тело вращается с угловой скоростью  . Вычислим мощность и работу силы. Точка приложения силы описывает окружность. Разложим силу на составляющие по осям естественного трехгранника (Рис. 5.4):
. Вычислим мощность и работу силы. Точка приложения силы описывает окружность. Разложим силу на составляющие по осям естественного трехгранника (Рис. 5.4):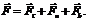 Работу будет совершать только составляющая
Работу будет совершать только составляющая  , направленная по касательной к траектории точки M:
, направленная по касательной к траектории точки M: 
 где
где 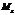 – момент силы
– момент силы  или
или 
 (5.6)
(5.6)