
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
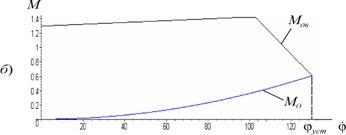
Усталений режим. Нерівномірність руху механізмуГоловною ознакою роботи машини в усталеному режимі є сталість середньої швидкості обертання двигуна та виконавчого органу. Це можливо лише за умови рівності приведеного до вала двигуна моменту сил опору робочої машини та обертового моменту двигуна. Цей факт наочно демонструють графіки на рис. 5.5, а, б. Звичайно мається на увазі проміжок часу, більший за цикл усталеного руху. Так, для останнього прикладу підрозділу 5.5 можна записати, що при усталеному режимі руху має виконуватися рівність
де
Рис. 5.5
Враховуючи, що рівняння прямої, яка проходить через дві точки, має вигляд Звідки Звернемо увагу на те, що апроксимуюча крива проходить не через ті точки, які взято у прикладі попереднього підрозділу (тобто, наведено інший спосіб ідеалізації статичної характеристики двигуна для усталеного режиму руху). Тоді формулу для усталеної швидкості можна подати у вигляді
У розглядуваному прикладі швидкість є сталою (частковий випадок). Це є наслідком того, що як моменти, які прикладені до ланки зведення, так і зведений момент інерції машини є також сталі (не залежать від кутової координати вала). Усталеним режимом руху називається такий рух, при якому швидкість початкової ланки (узагальнена швидкість) є періодичною функцією часу. На рис. 5.2 показано типовий приклад залежності швидкості руху початкової ланки механізму від часу t. Як бачимо, для усталеного режиму руху, кутова швидкість періодично коливається відносно деякого постійного середнього значення. 
Рис. 5.6 Нерівномірність ходу машини є наслідком двох факторів: зміни упродовж циклу миттєвих значень зведених моментів рушійних сил і сил опору; періодичної зміни зведеного моменту інерції механізму. Нерівномірність обертання оцінюється коефіцієнтом нерівномірності
де Величина Коефіцієнт нерівномірності характеризує розмах коливань швидкості по відношенню до її середнього значення. Очевидно, що чим менше Для кожного виду машин є своя допустима величина коефіцієнта нерівномірності Коефіцієнт нерівномірності є величина досить мала, що дозволяє прийняти середню величину кутової швидкості рівною середньому арифметичному з її максимального і мінімального значень. Звичайно, при проектуванні механізму задаються наперед бажаними для механізму значеннями коефіцієнта нерівномірності руху та середньої швидкості обертання головного вала. В усталеному режимі працюють дуже багато машин. Найкращі умови для роботи таких машин – абсолютно рівномірне обертання їх головного вала. Як відомо, у загальному випадку швидкість початкової ланки механізму при усталеному русі є змінною величиною. Коливання швидкості початкової ланки за час усталеного руху бувають двох різних типів: періодичні та неперіодичні. Періодичними коливаннями швидкостей машини називаються коливання, при яких швидкості всіх ланок машини в усіх їхніх положеннях мають цілком певні цикли, після закінчення яких ці швидкості набувають щоразу своїх початкових значень. Неперіодичні коливання швидкостей залежать від різних причин: раптової зміни корисних або шкідливих опорів, включення в машину додаткових мас і т.п. Раптова зміна навантаження на машину спричиняє раптове збільшення або зменшення швидкості головного вала машини і, оскільки ці коливання не мають певного циклу, то вони називаються неперіодичними. У більшості машин спостерігаються обидва види коливань швидкості. Коливання швидкості обох типів небажані як з точки зору динаміки машини, так і виконання нею технологічного процесу. Коливання швидкості спричиняють у кінематичних парах додаткові динамічні тиски, що знижують ККД машини, довговічність та надійність її роботи. Оскільки коливання швидкості повністю усунути неможливо, необхідно по можливості їх зменшити. Задача про регулювання швидкостей під час усталеного руху машини або механізму має суттєве практичне значення в техніці, оскільки в більшості машин цей час є робочим часом її руху, тобто проміжком часу, протягом якого машина долає виробничі опори. Розглянемо шляхи розв’язування цієї задачі. Маса є мірою інертності тіла. Всі ланки механізму мають інертність. Ця властивість полягає в тому, що чим інертніше матеріальне тіло, тим повільніше проходить зміна його швидкості, яка викликана дією прикладених до нього сил. Таким чином, щоб отримати обертання головного вала з нерівномірністю, що не перевищує заданої величини, інертність цього вала з усіма зв’язаними з ним деталями необхідно зробити достатньо великою. Практично, це збільшення інертності досягається посадкою на один із валів машини додаткової деталі, що має певний момент інерції. Ця деталь має назву маховик (колесо з великим моментом інерції). Підбираючи момент інерції маховика, можна забезпечити обертання головного вала машини із заданим коефіцієнтом нерівномірності. Дія маховика полягає у тому, що при перевищенні роботи Маховик є ніби акумулятором кінетичної енергії машини. Таким чином, основне призначення маховика є обмеження коливань кутової швидкості в межах, що встановлені величиною коефіцієнта нерівномірності Акумулююча здатність маховика використовується не лише для забезпечення допустимої нерівномірності ходу машини. В деяких машинах (у яких корисне навантаження періодично змінюється в значних межах) махових дозволяє використовувати накопичену енергію для подолання пікових корисних навантажень без збільшення потужності двигуна. Маховик неодмінно застосовується в машинах ударної дії – молотах, прокатних станах, дробарках і т. ін., допомагаючи електродвигуну при пікових навантаженнях. В автомобілях маховик сприяє рушати машині з місця. Регулювання періодичних коливань швидкості здійснюється за допомогою маховика виконаного, як правило, у вигляді колеса з розвинутим ободом (з великим моментом інерції). Регулювання неперіодичних коливань за допомогою маховика можливо здійснити, якщо вони незначні. При значних неперіодичних коливаннях встановлюють механізми, що називаються регуляторами – які регулюють закони зміни рушійних сил або сил опору. 5.7. Визначення моменту інерції маховика методом
Переходимо до наступної важливої задачі динаміки механізмів та машин - визначення найвигідніших співвідношень між силами, масами та швидкостями ланок механізму, які забезпечують заданий режим його руху. Визначення моменту інерції маховика за заданою величиною коефіцієнта нерівномірності Для машин, що виконують різні технологічні процеси, коливання Розглянемо задачу, в якій необхідно знайти величину зведеного моменту інерції ланки зведення, при якому її кутова швидкість не виходила б за наперед задані значення. Розв’язок даної задачі зводиться до визначення моменту інерції маховика. Задачу будемо розв’язувати методом Віттенбауера, графоаналітичним методом за допомогою побудови діаграми енергомас – залежності кінетичної енергії механізму від зведеного моменту інерції. Зазначимо, що метод Віттенбауера дозволяє при силах, що залежать від положень ланок, у наочній формі показати, як змінюється кутова швидкість початкової ланки та кінетична енергія механізму при зміні зведеного момента інерції. Для визначення моменту інерції махового колеса вважають заданими або попередньо знайденими: - схема механізму та розміри ланок; - маси і моменти інерції ланок; - середня кутова швидкість ланки зведення - коефіцієнт - сили, прикладені до ланок механізму. Виберемо за початкову ланку головний вал механізму, що виконує неперервний обертальний рух. Послідовність визначення моменту інерції маховика за методом Віттенбауера: - будуються п (дванадцять) рівновіддалених за кутом повороту кривошипа планів положень механізму; - для побудованих планів положень будуються плани швидкостей; - для п положень механізму за формулою (4) визначаються зведені моменти сил, при цьому для робочих машин знаходяться зведені моменти сил корисного опору М0, а зведені моменти рушійних сил Мр наближено приймаються такими, що мають деяке постійне значення, поки що невідоме. Для машин – двигунів, навпаки, знаходяться зведені Мр, а М0 приймаються постійними; - будується графік зведеного моменту сил корисного опору (для машин двигунів - рушійних сил) (рис. 5.7, а). Всі графіки будуються для одного циклу усталеного руху. - графічно інтегруючи зведений момент сил корисного опору, отримуємо графік робіт сил опору - віднявши від ординат графіка робіт рушійних сил ординати робіт сил корисного опору, будуємо графік надлишкової роботи, який одночасно є графіком приросту кінетичної енергії (рис. 5.3, в). - для побудованих положень механізму за формулою (7) визначаємо зведені до кривошипа моменти інерції механізму (без маховика) Зауважимо, що в результаті виконання перших трьох пунктів та даного – механізм приводиться до динамічної моделі; - будуємо графік зведеного моменту інерції як функцію кута повороту кривошипа, розмістивши вісь ординат перпендикулярно до осі ординат на попередніх графіках (рис. 5.3, г); - шляхом графічного виключення спільного параметра Підкреслимо, що цю діаграму накреслено для механізму без маховика. Такою ж діаграма залишиться і для механізму з маховиком. Але початок осей координат зміститься: вліво, оскільки зведений момент інерції буде більшим на величину моменту інерції маховика; і до низу, оскільки за такої ж самої - до кривої діаграми енергомас проводяться дві дотичні під кутами де Точка перетину дотичних є початком нової системи координат діаграми енергомас механізму з маховиком. Величина моменту інерції маховика визначається за формулою
де При малих значення коефіцієнта
де kl – відстань по осі ординат діаграми енергомас. Зазначимо, що для зменшення маси та габаритів маховика доцільніше його встановлювати на найшвидкохіднішому валі, оскільки кінетична енергія маховика, в результаті зміни якої здійснюється регулювання швидкості, прямо пропорційна
звідки де Іі – момент інерції маховика, встановленого на і-й ланці; Після визначення моменту інерції маховика та місця його встановлення розраховують його основі розміри. Відмітимо, що за допомогою кривої енергомас легко встановити залежність кутової швидкості ланки зведення як функції кута повороту
За формулою (19) будують графік Відмітимо також, що за допомогою кривої енергомас можна визначити коефіцієнт нерівномірності руху механізму. Для цього з початку системи координат (т.О1, рис. 5.3, д) проводимо дві дотичні до кривої енергомас. Вимірюємо кути
Визначення розмірів маховика.Форма маховика, загалом може бути вибрана довільною. Але за конструктивними міркуваннями, найбільш зручною є форма у вигляді диска з важким ободом, колеса зі спицями або форма, яка симетрична відносно головних осей інерції. При цій формі найлегше досягається співпадання осі обертання з однією із головних центральних осей інерції. Це дозволяє уникнути додаткових тисків на вальниці вала, на якому розміщений маховик. Якщо маховик виконаний у вигляді колеса зі спицями (рис. 5.4), то моментами інерції з’єднувальних частин нехтують і наближено вважають , що маса маховика рівномірно розподілена по колу радіуса
де m – маса маховика.
Рис. 5.4 Добуток маси обода маховика на квадрат його діаметра З рівняння (19) випливає, що при визначеній величині Iм вага маховика обернено пропорційна квадрату його діаметра D і для зменшення металоємкості вигідно брати більші діаметри. Але це заперечує вимозі малих габаритів та лімітується допустимою кутовою швидкістю. Для запобігання небезпеці можливого розриву маховика відцентровими силами його діаметр D вибирають таким чином, щоб колова швидкість на ободі не перевищувала допустиму для матеріалу маховика величину. Для перевірки діаметра маховика можна рекомендувати таку залежність:
де Маса обода маховика практично може бути взята тоді ширина b обода визначається з виразу
Тут с = 0.4b; ЗРІВНОВАЖЕННЯ МЕХАНІЗМІВ Зрівноваження додаткових динамічних сил (сил інерції), які виникають при русі механізмів і машин, є однією з найважливіших задач сучасного машинобудування. Це пов’язано з тим, що ланки механізмів, як правило, рухаються з прискоренням, в результаті чого виникають сили інерції, які викликають додаткові, часом досить великі, навантаження у кінематичних парах. Особливо це стосується швидкохідних машин. Ці змінні як за величиною, так і за напрямком сили, передаються станині (корпусу) машини, фундаменту, викликають їх вібрацію, коливання та розхитування. Найбільш небезпечними є вібрації у зоні, близькій до резонансу, вони можуть викликати руйнування деталей машин та механізмів. Тому впроцесі проектування та виготовлення машин ставиться завдання про зрівноваження динамічних сил. Необхідно добитися, щоб на корпус і фундамент машини передавались тиски, постійні за величиною та напрямом. Ця задача називається задачею про зрівноваження рухомих мас механізмів або про зрівноваження динамічних сил інерції. Розв’язати її можна шляхом раціонального підбору та розміщення мас ланок. Задачу про зрівноваження сил інерції в машинах можна поділити на дві окремі задачі: 1. зрівноваження механізму вцілому (задача про зрівноваження динамічних навантажень на фундамент машин); 2. зрівноваження окремих обертових ланок механізму (задача про зрівноваження додаткових динамічних тисків у кінематичних парах механізму). |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 339. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 . Оскільки, стійка ділянка характеристики асинхронного двигуна може бути апроксимована лінійною залежністю
. Оскільки, стійка ділянка характеристики асинхронного двигуна може бути апроксимована лінійною залежністю  , то
, то ,
, – сталі коефіцієнти.
– сталі коефіцієнти.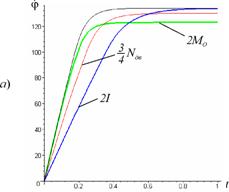
 , можна записати
, можна записати  (рис. 5.6), або
(рис. 5.6), або  .
. ,
,  .
. .
.
 ,
, - відповідно, максимальна, мінімальна та середня за цикл швидкість.
- відповідно, максимальна, мінімальна та середня за цикл швидкість. рахується за формулою
рахується за формулою  , у якій n – частота обертання початкової ланки.
, у якій n – частота обертання початкової ланки. , тим рівномірніше рухається початкова ланка.
, тим рівномірніше рухається початкова ланка. , встановлена практикою. Значення допустимих коефіцієнтів нерівномірності руху наведено у технічних довідниках; так для помпи 1/5-1/30; для металообробних верстатів 1/20-1/50, для ДВЗ 1/80-1/100, для електричних генераторів змінного струму 1/200-1/300, для авіаційних двигунів та турбогенераторів 1/200 і менше.
, встановлена практикою. Значення допустимих коефіцієнтів нерівномірності руху наведено у технічних довідниках; так для помпи 1/5-1/30; для металообробних верстатів 1/20-1/50, для ДВЗ 1/80-1/100, для електричних генераторів змінного струму 1/200-1/300, для авіаційних двигунів та турбогенераторів 1/200 і менше. над роботою
над роботою  маховик приймає на себе надлишок кінетичної енергії механізму і, завдяки своєму великому моменту інерції, не дає швидкості надмірно зростати; коли ж робота
маховик приймає на себе надлишок кінетичної енергії механізму і, завдяки своєму великому моменту інерції, не дає швидкості надмірно зростати; коли ж робота 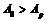 , маховик віддає накопичену кінетичну енергію, протидіючи зменшенню швидкості.
, маховик віддає накопичену кінетичну енергію, протидіючи зменшенню швидкості.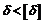 виконується у процесі проектування машини та складає одну із задач її динамічного синтезу.
виконується у процесі проектування машини та складає одну із задач її динамічного синтезу.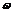 допустимі лише в певних межах, встановлених практикою експлуатації обладнання.
допустимі лише в певних межах, встановлених практикою експлуатації обладнання. . Графік робіт рушійних сил для робочих машин з урахуванням прийнятих припущень, а також беручи до уваги те, що за один цикл усталеного руху АР=АО, що являє собою пряму лінію, яка з’єднує початок і кінець графіка роботи сил опору (рис. 5.3, б) (для машин-двигунів навпаки);
. Графік робіт рушійних сил для робочих машин з урахуванням прийнятих припущень, а також беручи до уваги те, що за один цикл усталеного руху АР=АО, що являє собою пряму лінію, яка з’єднує початок і кінець графіка роботи сил опору (рис. 5.3, б) (для машин-двигунів навпаки); ;
;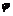 з діаграм приросту кінетичної енергії та зведеного моменту інерції будуємо графік приросту кінетичної енергії як функції зведеного моменту інерції – діаграму енергомас (рис. 5.3, д).
з діаграм приросту кінетичної енергії та зведеного моменту інерції будуємо графік приросту кінетичної енергії як функції зведеного моменту інерції – діаграму енергомас (рис. 5.3, д).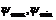 до осі
до осі  ,
, ,
, 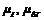 - відповідно масштаби по осі абсцис і ординат діаграми енергомас.
- відповідно масштаби по осі абсцис і ординат діаграми енергомас. ,
,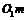 - відстань, на яку зміститься вісь ординат.
- відстань, на яку зміститься вісь ординат. ,
,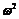 . Якщо маховик встановлюється не на ланці зведення, а на іншій ланці механізму, то повинна задовольнятися умова рівності кінетичної енергії
. Якщо маховик встановлюється не на ланці зведення, а на іншій ланці механізму, то повинна задовольнятися умова рівності кінетичної енергії ,
,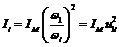 ,
,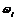 - кутова швидкість цієї ланки;
- кутова швидкість цієї ланки;  - передатне відношення. Таким чином, чим більша кутова швидкість і-ї ланки, тим менший момент інерції маховика, і, відповідно менші його маса та габарити.
- передатне відношення. Таким чином, чим більша кутова швидкість і-ї ланки, тим менший момент інерції маховика, і, відповідно менші його маса та габарити.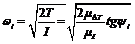 . (19)
. (19) . Порівнюючи між собою кути
. Порівнюючи між собою кути 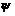 , можна наочно прослідкувати, як змінюється кутова швидкість ланки зведення при зміні її положення.
, можна наочно прослідкувати, як змінюється кутова швидкість ланки зведення при зміні її положення. . Коефіцієнт нерівномірності руху визначаємо за формулою
. Коефіцієнт нерівномірності руху визначаємо за формулою .
. - геометричному місцю центрів ваги поперечних перерізів обода. Тоді момент інерції маховика можна виразити так (використовується формула для моменту інерції тонкого кільця):
- геометричному місцю центрів ваги поперечних перерізів обода. Тоді момент інерції маховика можна виразити так (використовується формула для моменту інерції тонкого кільця): (20)
(20)
 називається маховим моментомабо характеристикоюмаховика. Для багатьох деталей машин, що здійснюють обертальний рух (муфти, ротори електродвигунів тощо), ця характеристика наводиться у довідниках. Характеристика маховика має одиницю виміру кг·м2. За цією характеристикою можна визначити необхідну масу маховика, якщо задано або вибрано його діаметр, значення якого визначається з суто конструктивних міркувань.
називається маховим моментомабо характеристикоюмаховика. Для багатьох деталей машин, що здійснюють обертальний рух (муфти, ротори електродвигунів тощо), ця характеристика наводиться у довідниках. Характеристика маховика має одиницю виміру кг·м2. За цією характеристикою можна визначити необхідну масу маховика, якщо задано або вибрано його діаметр, значення якого визначається з суто конструктивних міркувань. , (21)
, (21) - допустима колова швидкість обода маховика, яка не повинна перевищувати для сталевих маховиків 70 – 120 м/с, для чавунних - 30 – 45 м/с;
- допустима колова швидкість обода маховика, яка не повинна перевищувати для сталевих маховиків 70 – 120 м/с, для чавунних - 30 – 45 м/с;  - частота обертання маховика, хв-1. Зауважимо, що хромонікелеві маховики допускають колову швидкість до 150 м/с.
- частота обертання маховика, хв-1. Зауважимо, що хромонікелеві маховики допускають колову швидкість до 150 м/с. ,
,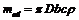 .
. - густина матеріалу, кг/м3; для сталевих маховиків (
- густина матеріалу, кг/м3; для сталевих маховиків ( 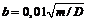 .
.