
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Механічний коефіцієнт корисної дії
Механічний коефіцієнт корисної дії (ККД) є важливою енергетичною характеристикою механізму і вказує на ефективність використання енергії в машині.
де Механічним ККД називають відношення роботи сил корисного опору до роботи рушійних сил за цикл усталеного руху, тобто
ККД є відношенням абсолютного значення роботи сил корисних опорів до роботи рушійних сил за цикл усталеного руху. Машина є тим досконаліша, чим більша частина роботи рушійних сил витрачається на подолання сил корисних опорів та чим менша частина витрачається на подолання сил шкідливих опорів, тобто чим більший ККД. ККД звичайно визначається для усталеного періоду руху механізму. У випадку, якщо його величина є змінною, то визначають середню величину цього коефіцієнта. Переважно ККД окремих механізмів визначається експериментально та наводиться у довідниках. ККД групи механізмів (машин, кінематичних пар) залежить від з’єднання окремих складових. Механізми можуть бути з’єднані послідовно, паралельно і комбіновано. ККД групи послідовно з’єднаних механізмів. При послідовному з’єднанні (рис. 4.14, а) весь енергетичний потік проходить через усі механізми. Внаслідок того, що корисна робота попереднього механізму (витрачається на виробничий опір) є роботою рушійних сил для кожного наступного механізму, то
Загальний ККД
Таким чином, при послідовному з’єднанні загальний ККД дорівнює добутку ККД окремих механізмів. ККД групи паралельно з’єднаних механізмів. Нехай є машинний агрегат, який складається з n паралельно з’єднаних механізмів (рис. 4.14, б). Робота рушійних сил  Представимо ККД кожного з механізмів таким чином:
Тоді загальний ККД машинного агрегату при паралельному з’єднанні можна подати у наступному вигляді:
З формули (6) слідує, що загальний ККД, являє собою дріб, в якому чисельник та знаменник є, відповідно, сумами чисельників та знаменників часткових ККД механізмів, що входять до складу машинного агрегату. Відомо, що при утворенні таким чином дробу з декількох дробів, отримується число більше за найменше але менше за найбільше із значень дробів. Отже, і загальний ККД буде більшим за найменший частковий ККД, але меншим за найбільший частковий ККД,
а)
б) Рис. 4.14 Часткові випадки з’єднання механізмів. 1. Роботи рушійних сил розподіляються між окремими механізмами рівномірно,
тобто дорівнює середньому арифметичному окремих ККД, які входять до складу машинного агрегату. 2. ККД усіх механізмів однакові, тобто Відмітимо, що при паралельному з’єднанні механізмів, за інших рівних умов, є можливість отримати вищий ККД, ніж при послідовному з’єднанні. 5. ДОСЛІДЖЕННЯ РУХУ МАШИННОГО АГРЕГАТУ З ЖОРСТКИМИ ЛАНКАМИ
Вивчення закону руху машинного агрегату під дією заданих сил є однією з основних задач динаміки. Для розв’язку цієї задачі необхідно скласти рівняння руху системи і розв’язати його відносно невідомого кінематичного параметра. При визначенні закону руху задача може бути суттєво спрощена, якщо перейти до динамічної моделі. Отже, вивчення динаміки машинного агрегату повинно починатися з вибору динамічної моделі. Вибір динамічної моделі того чи іншого об’єкта залежить, у першу чергу, від його конструктивних особливостей, мети дослідження та характеру задачі, що розглядається. Найбільш простим способом ідеалізації є перехід від реального машинного агрегату до такого, що містить лише механізми з жорсткими ланками. При цьому виходять з таких припущень: усі ланки, які є твердими тілами рахуються абсолютно твердими; гнучкі ланки (паси, муфти і т.п.) – нерозтяжні; рідкі – такі, що не стискаються; усі кінематичні пари ідеально реалізують рівняння в’язей, якими вони описуються; відсутні зазори, поверхні вищих кінематичних пар, що дотикаються не деформуються і т.п. У жорсткому машинному агрегаті число ступенів вільності (тобто число незалежних параметрів, які однозначно визначають положення усіх ланок механічної системи) співпадає з числом ступенів рухомості. Зокрема, в жорсткому машинному агрегаті з одним двигуном координати усіх точок є функціями однієї узагальненої координати. Зазначимо, що дослідження руху машинного агрегату з урахуванням пружності ланок в конспекті не розглядається. Перший етап динамічного дослідження полягає в спрощенні вихідного об’єкта, тобто у заміні його деякою моделлю (схемою), у якій намагаються відобразити найбільш суттєві властивості розглядуваної механічної системи. Кожній фізичній моделі відповідає своя математична модель, тобто система диференціальних, інтегральних або інтегро-диференціальних рівнянь, за допомогою яких здійснюється математичне описання математичного об’єкту. Третім етапом динамічного розрахунку є розв’язання рівнянь, отриманих при складанні математичної моделі. При цьому використовуються як аналітичні так і чисельні методи. |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 544. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
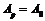 ,
,  – рівняння робіт за цикл усталеного руху,
– рівняння робіт за цикл усталеного руху, – робота рушійних сил, корисного та шкідливого опору.
– робота рушійних сил, корисного та шкідливого опору.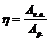 .
. ;
;  ;
;  ...
... 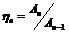 .
. (5)
(5) , яка підводиться до машинного агрегату, розподіляється якимось чином між окремими механізмами, A1, A2, A3, …, An. Звичайно
, яка підводиться до машинного агрегату, розподіляється якимось чином між окремими механізмами, A1, A2, A3, …, An. Звичайно 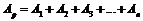 . Кожна з робіт A1, A2, A3, …, An є роботою рушійних сил для відповідного механізму.
. Кожна з робіт A1, A2, A3, …, An є роботою рушійних сил для відповідного механізму.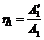 ,
,  ,
,  , ...,
, ..., 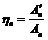 .
.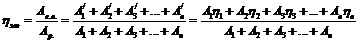 . (6)
. (6)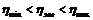 .
. З виразу (6) також випливає, що при паралельному з’єднанні механізмів загальний ККД машинного агрегату залежить не лише від ККД часткових механізмів, але й від характеру розподілу роботи рушійних сил між окремими механізмами.
З виразу (6) також випливає, що при паралельному з’єднанні механізмів загальний ККД машинного агрегату залежить не лише від ККД часткових механізмів, але й від характеру розподілу роботи рушійних сил між окремими механізмами.

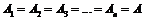 . Тоді загальний ККД, згідно з (6) матиме вигляд:
. Тоді загальний ККД, згідно з (6) матиме вигляд: ,
, , то загальний ККД машинного агрегату дорівнює ККД окремого механізму
, то загальний ККД машинного агрегату дорівнює ККД окремого механізму  .
.