
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ТЕРТЯ В МЕХАНІЗМАХ І МАШИНАХПід час роботи машин та механізмів має місце явище, яке перешкоджає рухові його ланок та супроводжується розсіюванням механічної енергії. Це явище називається тертям. Енергія, що витрачається на тертя, перетворюється у теплоту. Одночасно з цим відбувається згладжування шорсткостей поверхонь, що стикаються, тобто їхнє зношення (спрацювання). Підраховано, що біля третини світових енергетичних ресурсів даремно витрачається на роботу пов’язану з тертям. Цілком зрозуміло, що бажано щоб ці втрати були мінімальними. Також відомо, що більшість (80%) деталей машин виходять з ладу через зношення; забезпечити міцність деталей простіше та дешевше, ніж стійкість проти спрацювання. Тому ще з моменту виникнення ТММ як науки тертя було одним з перших розглядуваних питань. Відмітимо, що з іншого боку, тертя – корисне явище, на використанні сил тертя ґрунтується робота багатьох машин і механізмів (рух транспортних засобів, пасової та фрикційної передач, фрикційних муфт, зчеплень, гальм). В наш час галузь науки, що охоплює комплекс питань, пов’язаних з тертям та спрацюванням деталей машин, має назву триботехніка. При дослідження фізичних основ явища тертя розрізняють тертя зовнішнє та внутрішнє. Зовнішнє тертя – опір відносному переміщенню, що виникає між двома тілами у зонах дотику їхніх поверхонь, по дотичній до них і що супроводжується дисипацією енергії. Внутрішнє тертя – процеси, що проходять у твердих (рідких та газоподібних тілах) при їх деформації і, що призводять до необоротного розсіювання механічної енергії. У ТММ розглядається зовнішнє тертя. Сили тертя – це сили, що виникають у кінематичних парах при відносному русі ланок; вони обумовлені реакціями в’язей і є складовими цих реакцій.  Тертя – це складне фізичне явище, для пояснення якого запропоновані дві гіпотези: механічну та молекулярну. Згідно з першою гіпотезою, тертя виникає внаслідок деформацій невеликих виступів і западин які неодмінно є на поверхнях тертя (як би при цьому вони не були добре виготовлені). Згідно з іншою гіпотезою процес тертя полягає у подоланні існуючих та виникнення нових, сил молекулярної взаємодії у зонах фактичного контакту тіл. Таким чином, сила тертя виникає внаслідок механічного зачеплення, пружно-пластичної деформації та молекулярної взаємодії контактуючих елементів поверхонь тертя. Види тертя. Залежно від характеру відносного руху елементів кінематичних пар розрізняють: тертя ковзання (тертя першого роду); тертя кочення (тертя другого роду); тертя вертіння. Інколи відрізняють ще тертя кочення з проковзуванням та тертя при вібропереміщеннях. Для зменшення сил тертя та інтенсивності спрацювання елементів кінематичних пар використовують мастила. За станом поверхонь тертя розрізняють два види тертя: сухе тертя (без мастила) і тертя з мастилом. В іншій літературі часто трапляється такий поділ – сухе тертя та рідинне (в’язке) тертя. Сухе – це тертя, що виникає на поверхнях вільних від будь-яких сторонніх речовин. Рідинне – тертя, при якому поверхні тертя повністю розділені шаром мастила. Сили сухого та рідинного тертя мають різну природу, тому методи їх розрахунку різні. Крім того, інколи ще розрізняють проміжні види тертя: граничне, напівсухе і напіврідинне. Тертя ковзання сухих тіл Тертям називають опір, який виникає при русі або намаганні рухатися одного тіла по поверхні іншого. Елементарне уявлення про розподіл сил при терті ковзання сухих тіл можна встановити розглядаючи простий приклад. Нехай повзун 1 вагою
a) б) Рис. 4.1 Таким чином тертю руху передує тертя спокою, тобто сила тертя між тілами 1 і 2 діє при їхньому відносному мікрозміщенні. Сила тертя ковзання спокою перебуває в спільній дотичній площині до поверхонь тіл, що дотикаються, і спрямована протилежно до напрямку їх можливого переміщення під дією активних сил. Її модуль залежить від активних сил і може приймати значення в межах від нуля до певної величини Сила тертя, яка перешкоджає ковзанню тіла, під час його руху, називається силою тертя руху, або динамічною силою тертя ковзання. Як показують досліди, сила тертя руху менша від статичної сили тертя. У більшості технічних розрахунків користуються наближеними законами тертя ковзання встановленими Г. Амонтоном і Ш. Кулоном. 1. Сила тертя при інших рівних умовах не залежить від площі дотику поверхонь тертя. 2. Максимальне значення сили тертя спокою прямо пропорційне до нормальної реакції N (нормального тиску)
де Коефіцієнт тертя ковзання спокою є безрозмірною величиною, яка залежить матеріалу поверхонь тіл, що контактують, і їх фізичного стану, тобто від величини і характеру Зауважимо, що матеріали які мають високий коефіцієнт тертя, називають фрикційними (гума, текстоліт, азбест, шкіра, тощо) і, навпаки, низький коефіцієнт тертя – антифрикційними (бронза, латунь, бабіт, сірий чавун, капрон, і деякі інші види пластмас). 3. Сила тертя зростає із збільшенням часу попереднього контакту ланок. Величину сили тертя руху визначають за формулою аналогічною до (1), підставивши в неї замість коефіцієнта тертя спокою fc коефіцієнт тертя руху
де f – динамічний коефіцієнт тертя ковзання, безрозмірна величина, що визначається експериментально. У технічних розрахунках вважають, що динамічний коефіцієнт тертя ковзання не залежить від відносної швидкості руху тіл. Значення коефіцієнта тертя наведено у довідниках, часто приймають Отже, сила тертя ковзання пропорційна нормальному тиску N, прикладена на поверхні стику деталей і направлені у бік, протилежний швидкості їхнього відносного руху. Звичайно, сили тертя, що виникають на поверхні взаємодіючих тіл, завжди з’являються попарно: одна з них прикладена до одного тіла, а інша – до другого тіла і напрямлена у зворотній бік.
Рис. 4.2
Кут і конус тертя. Таким чином, повна реакція шорсткої поверхні R визначається діагоналлю паралелограма , побудованій на нормальній реакції N і силі тертя Нехай усі зовнішні сили, що діють на повзун, на негладкій поверхні враховуючи і його вагу, зводяться до рівнодіючої Q, яка проходить через т.A дотику повзуна з опорною поверхнею і утворюють з нормаллю до цієї поверхні кут
Рис. 4.3 Оскільки опорна поверхня шорстка, то при дії сили Q крім нормальної реакції Для того, щоб повзун рухався по напрямній, необхідно витримати умову:
Оскільки відносний рух у напрямку спільної нормалі відсутній, то Звідси знайдемо необхідну умову можливості руху повзуна по напрямній, Якщо повзун будемо пересувати відносно опорної поверхні у різні боки, то лінія реакції Викладене про тертя ковзання стосується лише сухого тертя. У випадках в’язкого тертя, тобто якщо на поверхнях тертя є мастило, користуються іншими закономірностями. Тертя в клиновій поступальній парі. Для надання повзуну строго прямолінійного руху без бічних відхилень застосовують клинові (клинчасті) напрямні. У цих випадках поверхня стикання повзуна і напрямної має в поперечному перерізі вигляд симетричного двогранного кута, або жолоба (рис. 4.4, а). При цьому зовнішнє навантаження сприймається двома поверхнями. Таку кінематичну пару називають клиновою.
Рис. 4.4 Для рівномірного руху повзуна має виконуватись умова
У випадку симетричного жолоба
Згідно з векторним рівнянням рівноваги усіх сил, що діють на повзун у поперечному перерізі З плану сил отримуємо: Тоді
де Отже, у всіх випадках, коли має місце тертя в клиновій парі, можна користуватися формулами для плоскої поступальної кінематичної пари, в які замість коефіцієнта тертя Оскільки завжди Коефіцієнт
Із (2) видно, що сила тертя повзуна в циліндричній напрямній на 27% більша за силу тертя в плоскій поступальній парі. Однак, враховуючи простоту виготовлення, циліндричні поступальні пари досить широко використовуються в техніці. Тертя у гвинтовій кінематичній парі. Гвинтові пари знайшли широке застосування у машинах і приладах, наприклад, у кріпильних різьбових з’єднаннях (кріпильні болти), у токарних верстатах (ходові гвинти), у домкратах, пресах, лещатах, струбцинах і т ін. Основними геометричними параметрами різьби є Крутний (рушійний) момент можна подати як добуток сили на плече:
де
Рис. 4.5 Вважаємо, що тиск гайки на гвинт (і гвинта на гайку) прикладений по середній лінії різьби. Дію сил у гвинтовій парі зведемо до дії сил на повзун, що розміщений на похилій площині, у якої кут нахилу дорівнює куту підйому гвинтової лінії. Цим самим, зведемо просторову задачу до плоскої. Знайдемо рушійну силу
Будуємо трикутник сил у певному масштабі (рис. 4.6), з якого знаходимо невідомі Силу
звідки матимемо
де Умовою самогальмування гвинтів, за аналогією з похилою площиною, буде
Тертя у гвинтах з трикутною різьбою. Для гвинтів з трикутною різьбою формула для визначення крутного моменту
Рис. 4.6
Враховуючи те, що тертя у гвинтах з трикутною різьбою ототожнюється з тертям на похилій площині з клинчастою напрямною, слід ввести у формули зведені коефіцієнти та кути тертя
де Тертя в обертових кінематичних парах. Опорні частини валів та осейназиваються цапфами. Цапфи, розміщені на кінцях валів, називають шипами, а проміжні – шийками. Нерухому ланку обертової кінематичної пари, що підтримує шип або шийку, називають підшипником. Шипи та шийки сприймають радіальне навантаження. Частини валів (осей), які сприймають осьові навантаження називають п’ятами. В обертовій парі (рис. 4.7) лінія дії результуючої реакції Радіус круга тертя дорівнює
де Для непритертих цапф Момент
Рис. 4.7
Тертя гнучкої ланки У техніці широке застосування отримали механізми з гнучкими ланками: пасові, канатні передачі, стрічкові гальма та пили, транспортери. Формулу, що зв’язує основні параметри передачі гнучкою ланкою отримав в 1765 р. Л.Ейлер. При її виводі були прийняті такі припущення: гнучка ланка не розтягується і не чинить опору згину при набіганні і збіганні, вона рухається зі сталою швидкістю
Рис. 4.8 Формула Ейлера, що зв’язує параметри передачі гнучкою ланкою
де Сила тертя гнучкої ланки
При усталеному русі гнучкої ланки з постійною швидкістю різниця натягів збігаючого та набігаючого кінців дорівнює силі тертя між ниткою та шківом (рис. 4.8). Сила |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 422. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (рис. 4.1) перебуває на горизонтальній площині 2 у стані спокою,
(рис. 4.1) перебуває на горизонтальній площині 2 у стані спокою,  . Якщо прикласти до повзуна деяку невелику горизонтальну силу
. Якщо прикласти до повзуна деяку невелику горизонтальну силу 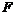 , він тим не менше залишається у спокої. Це свідчить про те, що на повзун 1, крім нормальної реакції
, він тим не менше залишається у спокої. Це свідчить про те, що на повзун 1, крім нормальної реакції  , з боку площини 2 діє ще одна сила –
, з боку площини 2 діє ще одна сила –  , яка зрівноважує прикладену силу
, яка зрівноважує прикладену силу  .
.
 , якої він досягне в момент виходу тіла зі стану спокою.
, якої він досягне в момент виходу тіла зі стану спокою.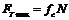 , (1)
, (1) - коефіцієнт тертя ковзання спокою.
- коефіцієнт тертя ковзання спокою.
 .
. ,
, .
.
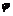 який називається кутом тертя. З рис. 4.2 маємо
який називається кутом тертя. З рис. 4.2 маємо  , з іншого боку
, з іншого боку  . Тангенс кута тертя дорівнює коефіцієнту тертя ковзання. Отже, наявність тертя змінює величину та напрям діючих сил; повна реакція напрямної на повзун відхилена від спільної нормалі до їхніх поверхонь (а не напрямлена вздовж неї) в бік протилежний до швидкості повзуна на кут тертя.
. Тангенс кута тертя дорівнює коефіцієнту тертя ковзання. Отже, наявність тертя змінює величину та напрям діючих сил; повна реакція напрямної на повзун відхилена від спільної нормалі до їхніх поверхонь (а не напрямлена вздовж неї) в бік протилежний до швидкості повзуна на кут тертя. (рис. 4.3). Перенесемо дану силу по лінії дії в т. A та розкладемо її на дві складові: нормальну до поверхні
(рис. 4.3). Перенесемо дану силу по лінії дії в т. A та розкладемо її на дві складові: нормальну до поверхні  і дотичну
і дотичну  .
.
 , або
, або  .
. і, отже,
і, отже,  .
. . Якщо ж,
. Якщо ж,  , то повзун буде знаходитися у стані спокою незалежно від величини прикладеної до нього сили. Цим пояснюється відоме явище заклинювання, або самогальмування.
, то повзун буде знаходитися у стані спокою незалежно від величини прикладеної до нього сили. Цим пояснюється відоме явище заклинювання, або самогальмування. опише конічну поверхню, яка називається конусом тертя.
опише конічну поверхню, яка називається конусом тертя.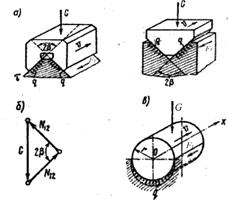
 .
. . Таким чином, сила тертя визначається за формулою
. Таким чином, сила тертя визначається за формулою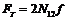 .
. , будуємо трикутник сил (рис. 4.4, б)
, будуємо трикутник сил (рис. 4.4, б) .
. ,
,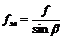 – зведений (умовний) коефіцієнт тертя клинової пари.
– зведений (умовний) коефіцієнт тертя клинової пари. підставляємо зведений коефіцієнт тертя.
підставляємо зведений коефіцієнт тертя. менший за
менший за  , то
, то  – коефіцієнта тертя плоскої поступальної пари. Цю властивість клинової пари широко використовують у техніці для збільшення сили тертя при передачі руху (наприклад, у пасових і фрикційних передачах, гвинтових з’єднаннях).
– коефіцієнта тертя плоскої поступальної пари. Цю властивість клинової пари широко використовують у техніці для збільшення сили тертя при передачі руху (наприклад, у пасових і фрикційних передачах, гвинтових з’єднаннях). використовується також у формулах розрахунку сили тертя і в циліндричній поступальній парі
використовується також у формулах розрахунку сили тертя і в циліндричній поступальній парі . (2)
. (2) ,
, 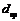 та
та  – зовнішній, середній та внутрішній діаметри,
– зовнішній, середній та внутрішній діаметри,  – висота підйому середньої гвинтової лінії різьби,
– висота підйому середньої гвинтової лінії різьби, 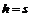 , де
, де  – крок різьби; у багатозахідних
– крок різьби; у багатозахідних  , де
, де  – число заходів. Із розгортки на площину середньої гвинтової лінії випливає, що
– число заходів. Із розгортки на площину середньої гвинтової лінії випливає, що  .
. ,
,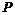 – прикладена до гайки рушійна сила, необхідна для її рівномірного переміщення;
– прикладена до гайки рушійна сила, необхідна для її рівномірного переміщення;  – довжина плеча.
– довжина плеча.
 .
.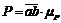 ;
; 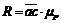 .
.
 ,
,
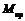 та умова самогальмування за зовнішнім виглядом такі самі, як і для гвинтів із прямокутною різьбою. З рис. 4.6 не важко отримати формулу для визначення сили тертя
та умова самогальмування за зовнішнім виглядом такі самі, як і для гвинтів із прямокутною різьбою. З рис. 4.6 не важко отримати формулу для визначення сили тертя .
.
 ,
, – кут профілю різьби.
– кут профілю різьби. з боку ланки 1 (цапфи) на ланку 2 (вал) не проходить через центр
з боку ланки 1 (цапфи) на ланку 2 (вал) не проходить через центр  цапфи, а буде дотичною до круга тертя (на рис. 4.7 заштрихований) і відхиленою від нормальної реакції
цапфи, а буде дотичною до круга тертя (на рис. 4.7 заштрихований) і відхиленою від нормальної реакції 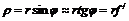 ,
,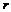 – радіус цапфи вала 2;
– радіус цапфи вала 2;  – зведений коефіцієнт тертя в обертовій кінематичній парі.
– зведений коефіцієнт тертя в обертовій кінематичній парі.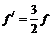 , для притертих цапф
, для притертих цапф  , де
, де  , який необхідно прикласти для повороту вала 2 в підшипнику 1, буде дорівнювати
, який необхідно прикласти для повороту вала 2 в підшипнику 1, буде дорівнювати .
.

 , її масою та відцентровою силами нехтуємо.
, її масою та відцентровою силами нехтуємо.
 ,
, – натяг набігаючого кінця;
– натяг набігаючого кінця;  – натяг збігаю чого кінця.
– натяг збігаю чого кінця. .
.