
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Краткие теоретические сведенияСтр 1 из 22Следующая ⇒ Лабораторная работа № 1 «Изучение методов генерации псевдослучайных числовых последовательностей с равномерным законом распределения»
Цель работы: Изучить методы генерации псевдослучайных числовых последовательностей с равномерным законом распределения и способов их тестирования.
Краткие теоретические сведения При решении любой физической задачи возникает сложность учета всех факторов, влияющих на исход мысленного или физического эксперимента, например, учет влияния всех отражающих поверхностей и препятствий при расчете величины электромагнитного поля в месте расположения абонента в условиях урбанизированной (городской) среды. Зачастую учет большинства факторов невозможен и приводит к неоправданному усложнению решаемой задачи. В таких случаях наравне с исследуемым полезным сигналом (электрическим током или напряжением, электрической мощностью или напряженностью электрического и магнитного полей) вводят случайную составляющую сигнала с требуемыми статистическими характеристиками, наиболее точно отражающими физическую картину исследуемого явления. Под случайной величиной (СВ) понимают физическую величину, которая в эксперименте со случайным исходом может принимать то или иное значение. Изменение такой случайной величины со временем носит название случайного процесса (СП), а конкретный вид, принимаемый случайным процессом в эксперименте, называется реализацией. При проведении серии идентичных экспериментов формируется семейство реализаций. На рисунке 1.1 представлен пример такого семейства. Основной характеристикой СП является так называемая функция распределения, определить которую можно следующим образом. Зафиксируем некоторый момент времени 
Подсчитаем количество случаев
Рис. 1.1 – Семейство реализаций случайного процесса Данную функцию можно рассматривать как вероятность того, что случайный процесс
Рассмотрим два близких уровня
Очевидно, что их разность описывает вероятность того, что случайный процесс
Тогда предел вида:
называется плотностью вероятности распределения СВ. Функция распределения и плотность вероятности обладают очевидными свойствами:
На основе плотности вероятности определяются такие числовые характеристики СП как математическое ожидание и дисперсия:
С физической точки зрения математическое ожидание есть не что иное, как постоянная составляющая случайной величины (например, тока или напряжения), а дисперсия – средняя мощность флуктуационной составляющей случайной величины (за вычетом постоянной составляющей). Корень квадратный из дисперсии СВ носит название среднего квадратического значения (СКО):
Поскольку одномерная плотность вероятности
Двумерная плотность вероятности обладает следующими очевидными свойствами:
С помощью введенной таким образом двумерной плотности вероятности распределения СВ строится ее корреляционная функция:
Очевидна связь корреляционной функции и дисперсии СВ:
Важное место среди случайных процессов занимают так называемые стационарные СП. Для таких СП вероятностные характеристики не зависят от выбора точки отсчета времени. Различают СП стационарные в узком и широком смыслах. СП является стационарным в узком смысле, если его
Очевидно, что в этом случае математическое ожидание и дисперсия перестают зависеть от времени:
Корреляционная функция стационарного СП обладает рядом специфических свойств: - функция корреляции четная
- функция корреляции максимальна при
- при неограниченном росте
Более узкий класс СП представляют эргодические СП. Они относятся к стационарным СП и для них результат усреднения по ансамблю значений реализаций в данном сечении СП совпадает с результатом усреднения по времени в пределах одной бесконечно длинной реализации: - математическое ожидание
- дисперсия
- корреляционная функция
В зависимости от требуемых статистических характеристик случайной составляющей физической величины используют модели СВ с различными законами распределения: - равномерный (модель случайных изменений начальной фазы напряжения на выходе генератора, шума квантования на выходе аналого-цифрового преобразователя (АЦП)) - нормальный или Гаусса (модель теплового и дробового шумов радиоэлектронной аппаратуры, космического, атмосферного и теплового шумов Земли (аддитивный шум), погрешности измерений (для большинства измерительных приборов)); - Рэлея (модель медленных замираний радиосигналов при их распространении в атмосфере Земли (мультипликативный шум), сигнала на выходе амплитудного детектора); - Райса (модель амплитудных флуктуаций радиосигнала, в том числе в многолучевом канале распространения); - Лапласа (модель отказов электрорадиоаппаратуры). Равномерное распределение имеют СВ, значения которых заключены в ограниченном интервале, причем вероятность попадания в любую ее часть шириной Одномерная плотность вероятности равномерно распределенной СВ описывается выражением вида:
Одномерная функция распределения такой СВ описывается выражением вида:
а ее математическое ожидание и дисперсия равны:
Нормальное (гауссово) распределение имеют физические величины, подверженные влиянию большого числа случайных независимых факторов. Одномерная плотность вероятности таких СВ описывается выражением вида:
где Впервые нормальное распределение (как предел биномиального распределения) появилось в 1738 году в работе английского математика Абрахама де Муавра «Доктрина случайностей». Это было первое доказательство частного случая так называемой центральной предельной теоремы. А в 1809 году немецкий математик Карл Фридрих Гаусс в сочинении «Теория движения небесных тел» ввёл это распределение как возникающее в результате многократных измерений движения небесных тел. Однако только в 1812 году французский математик Пьер-Симон де Лаплас в теореме Муавра-Лапласа обобщил результат А. де Муавра. Одномерная функция распределения нормально распределенной СВ описывается выражением вида:
Распределение Рэлея имеют СВ, одномерная плотность вероятности которых описывается выражением вида:
Такому распределению удовлетворяет СВ вида Данное распределение впервые было введено в 1880 г. британским физиком Джоном Уильямом Стреттом (лордом Рэлеем) при решении задачи о сложении гармонических колебаний со случайными начальными фазами. Одномерная функция распределения такой СВ описывается выражением вида:
а ее математическое ожидание и дисперсия равны:
Распределение Райса имеют СВ, одномерная плотность вероятности которых описывается выражением вида:
где Такому распределению удовлетворяет СВ вида Данное распределение введено как обобщение распределения Рэлея американским ученым Стефаном Райсом в его работах «Математический анализ случайных шумов» и «Статистические свойства суммы гармонического сигнала и случайного шума» 1945 и 1948 гг. Математическое ожидание и дисперсия такой СВ могут быть определены в виде:
Данные выражения могут быть упрощены для случаев малого
Распределение Лапласа имеют СВ, одномерная плотность вероятности которых описывается выражением вида:
Такому распределению удовлетворяет СВ вида
Данное распределение проявляется при суммировании случайного числа случайных слагаемых. Одномерная функция распределения такой СВ описывается выражением вида:
а, ее математическое ожидание и дисперсия СВ равны:
При экспоненциальном распределении:
В качестве источников СВ могут рассматриваться физические шумы радиокомпонентов (тепловой и дробовой шумы в резисторе, стабилитрона или транзистора) или космическое излучение. Однако проведение физического эксперимента по оценке статистических характеристик работы радиоаппаратуры различного назначения дорогостояще и, как правило, трудно реализуемо. С технической точки зрения более простым является проведение имитационного моделирования с использованием пакетов прикладных программ. В этом случае для генерации случайных величин используют особые численные алгоритмы. Эти алгоритмы заранее определены а, следовательно, генерируют последовательность чисел, которая теоретически не может быть статистически случайной. Но при удачном выборе алгоритма, полученная численная последовательность (псевдослучайная) будет удовлетворять большинству критериев случайности. Одной из характеристик такой последовательности является период повторения, который должен быть больше рабочего интервала, из которого берутся псевдослучайные числа. Генератор псевдослучайных чисел включён в состав многих современных процессоров. Наиболее распространенными алгоритмами генерации псевдослучайных чисел являются линейный конгруэнтный метод и метод Фибоначчи с запаздываниями. |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 190. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и выберем произвольное значение СВ
и выберем произвольное значение СВ  (рисунок 1.1). Рассматривая реализации СП, установим, выполняется ли для каждой из них условие вида:
(рисунок 1.1). Рассматривая реализации СП, установим, выполняется ли для каждой из них условие вида: .
. , для которых это условие выполняется, и разделим на общее количество рассмотренных реализаций СП
, для которых это условие выполняется, и разделим на общее количество рассмотренных реализаций СП  . Тогда при неограниченном увеличении
. Тогда при неограниченном увеличении  результат будет описываться устойчивой функцией
результат будет описываться устойчивой функцией  , называемой функцией распределения:
, называемой функцией распределения: . (1.1)
. (1.1)
 не превысит уровень
не превысит уровень  в момент времени
в момент времени  :
: . (1.2)
. (1.2) . Для одного и того же момента времени
. Для одного и того же момента времени  и
и  .
. лежит в диапазоне
лежит в диапазоне  :
: .
. (1.3)
(1.3) , (1.4)
, (1.4) . (1.5)
. (1.5) , (1.6)
, (1.6) . (1.7)
. (1.7) . (1.8)
. (1.8) не описывает взаимосвязь отдельных сечений СП
не описывает взаимосвязь отдельных сечений СП 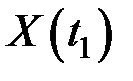 и
и  , то аналогичным образом могут быть введены двумерная функция распределения
, то аналогичным образом могут быть введены двумерная функция распределения  и двумерная плотность вероятности
и двумерная плотность вероятности  распределения СВ:
распределения СВ: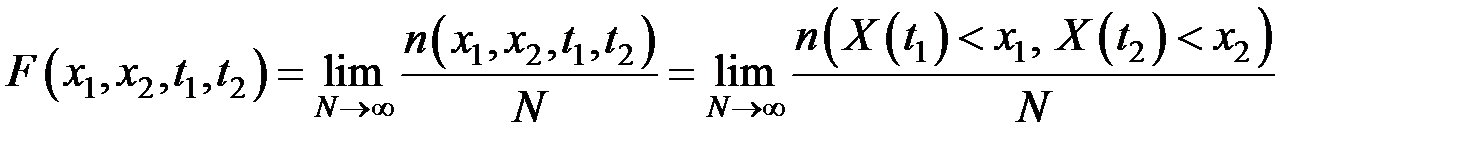 , (1.9)
, (1.9) . (1.10)
. (1.10)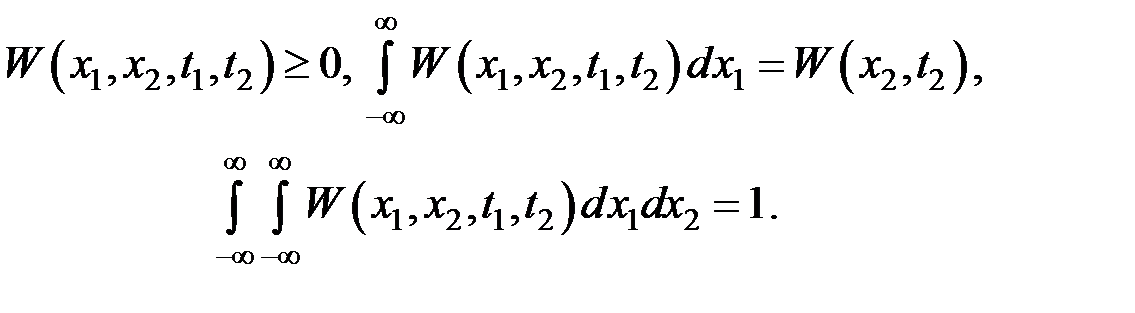 (1.11)
(1.11) (1.12)
(1.12) . (1.13)
. (1.13) -мерная плотность вероятности
-мерная плотность вероятности  зависит только от временных сдвигов
зависит только от временных сдвигов  . Для СП, стационарного в широком смысле, достаточно, чтобы его двумерная плотность вероятности
. Для СП, стационарного в широком смысле, достаточно, чтобы его двумерная плотность вероятности  зависела только от временного сдвига
зависела только от временного сдвига  :
: . (1.14)
. (1.14) ,
,  . (1.15)
. (1.15) , (1.16)
, (1.16)
 , (1.17)
, (1.17) функция корреляции убывает до нуля
функция корреляции убывает до нуля . (1.18)
. (1.18) , (1.19)
, (1.19)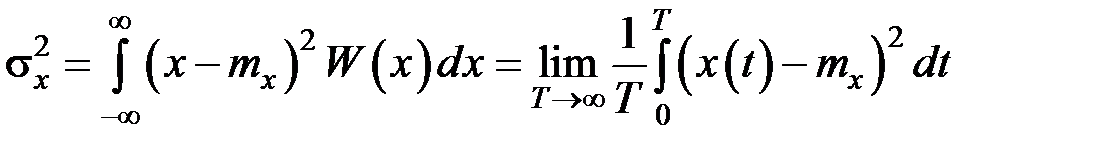 , (1.20)
, (1.20) (1.21)
(1.21) одинакова для всего интервала.
одинакова для всего интервала. (1.22)
(1.22) (1.23)
(1.23) ,
,  . (1.24)
. (1.24) , (1.25)
, (1.25) – математическое ожидание, а
– математическое ожидание, а  – дисперсия нормально распределенной СВ.
– дисперсия нормально распределенной СВ. , (1.26)
, (1.26) – функция Лапласа.
– функция Лапласа. . (1.27)
. (1.27) , если
, если  и
и  – нормально распределенные СВ с нулевыми математическими ожиданиями и одинаковыми дисперсиями
– нормально распределенные СВ с нулевыми математическими ожиданиями и одинаковыми дисперсиями  .
. , (1.28)
, (1.28) ,
,  . (1.29)
. (1.29) , (1.30)
, (1.30) – модифицированная функция Бесселя первого рода нулевого порядка.
– модифицированная функция Бесселя первого рода нулевого порядка.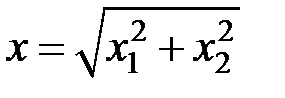 , если
, если 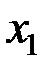 и
и  – нормально распределенные СВ с ненулевыми математическими ожиданиями
– нормально распределенные СВ с ненулевыми математическими ожиданиями  ,
,  и одинаковыми дисперсиями
и одинаковыми дисперсиями  причем
причем  .
.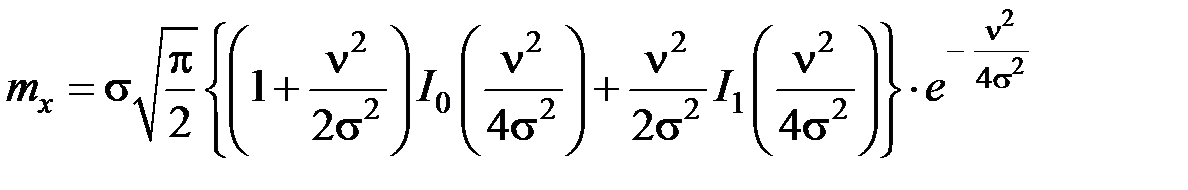 , (1.31)
, (1.31) . (1.32)
. (1.32) и большого
и большого  значений отношения сигнал шум (ОСШ):
значений отношения сигнал шум (ОСШ): (1.33)
(1.33) (1.34)
(1.34) . (1.35)
. (1.35)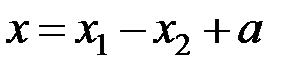 , если
, если  и
и  – экспоненциально распределенные СВ с одинаковым параметром
– экспоненциально распределенные СВ с одинаковым параметром  :
: ,
,  . (1.36)
. (1.36) (1.37)
(1.37) ,
, 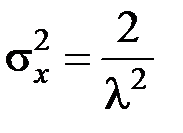 . (1.38)
. (1.38) ,
,  . (1.39)
. (1.39)