
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Краткие теоретические сведенияРассмотренные в предыдущей лабораторной работе методы генерации псевдослучайных последовательностей позволяют сформировать массивы отсчетов СВ с равномерным законом распределения. Однако при решении большинства практических задач требуется случайная (шумовая) составляющая с нормальным законом распределения. Основу всех методов преобразования равномерного закона распределения в любой другой закон составляет метод обратного преобразования функции распределения. Применение данного метода основано на нахождении функции, обратной по отношению к функции необходимого распределения. Если в качестве аргумента такой функции использовать равномерно распределенную на отрезке Поскольку функция распределения для гауссовой СВ не описывается в элементарных функциях, то найти для нее обратную функцию невозможно. Поэтому по отношению к данной задаче метод обратного преобразования функции распределения был модифицирован в трудах британского статистика Джорджа Бокса и Мервина Мюллера, опубликовавших работу в 1958 г. Авторами было замечено, что распределение суммы квадратов двух независимых нормально распределенных СВ подчиняется экспоненциальному закону и является частным случаем 
Рис. 2.1 – Расположение точки со случайными координатами на декартовой плоскости Таким образом, если координаты точки на декартовой плоскости будут распределены равномерно, то квадрат длины радиус-вектора, соединяющего точку с началом координат, будет распределен по экспоненциальному закону. Очевидно, что в любом направлении на декартовой плоскости найдется пара случайных величин Но тогда является справедливым и обратное утверждение. Если квадрат длины радиус-вектора точки на плоскости распределен по экспоненциальному закону, а угол, под которым радиус-вектор расположен к оси абсцисс, распределен равномерно в интервале Для получения процедуры преобразования равномерно распределенной СВ в экспоненциально распределенную воспользуемся одним из выражений (1.36), определяющих необходимый вид плотности распределения вероятности:
Тогда функция распределения будет иметь вид:
Функция, обратная по отношению к
С учетом того, что распределение СВ
Величина Угол, под которым радиус-вектор расположен к оси абсцисс, может быть сформирован из второй равномерно распределенной на интервале
Таким образом, декартовы координаты точки на плоскости равны:
и иметь нормальный закон распределения. Величина
где Решив систему уравнений (2.6) относительно
Тогда якобиан преобразования оказывается равным:
Учитывая, что
Тогда одномерная плотность распределения вероятности
Аналогичную плотность распределения вероятности имеет СВ
Сравнивая (2.9) и (2.10) с выражением (1.25) приходим к выводу, что СВ Таким образом, преобразование Бокса-Мюллера принимает вид:
Если требуется сформировать отсчеты СВ с другими числовыми характеристиками, то можно осуществить линейное преобразование вида:
где Существует модификация преобразования Бокса-Мюллера, позволяющая избавиться от вычислений тригонометрических функций. Она получается, если выразить
Тогда выражения (2.11) принимают вид:
Причем получаемые в результате значения будут вещественными, если:
Такое возможно, если точка с координатами Таким образом для выполнения преобразования Бокса-Мюллера вида (2.12) необходимо выбирать пару значений Недостатком данной модификации преобразования Бокса-Мюллера является необходимость отбрасывания части пар значений Лабораторное задание |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 220. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 случайную величину, то получится СВ с требуемым законом распределения.
случайную величину, то получится СВ с требуемым законом распределения. -распределения (или распределения Пирсона). С другой стороны такая сумма квадратов имеет простую геометрическую трактовку – это квадрат длины радиус-вектора, соединяющего начало системы координат с точкой на плоскости, причем декартовы координаты этой точки описываются значениями независимых СВ (рисунок 2.1).
-распределения (или распределения Пирсона). С другой стороны такая сумма квадратов имеет простую геометрическую трактовку – это квадрат длины радиус-вектора, соединяющего начало системы координат с точкой на плоскости, причем декартовы координаты этой точки описываются значениями независимых СВ (рисунок 2.1).
 , характеризующаяся одним и тем же значением квадрата длины радиус-вектора, а, значит, все значения угла
, характеризующаяся одним и тем же значением квадрата длины радиус-вектора, а, значит, все значения угла  равновероятны и распределены по равномерному закону в интервале
равновероятны и распределены по равномерному закону в интервале  .
. . (2.1)
. (2.1) . (2.2)
. (2.2) имеет вид:
имеет вид: . (2.3)
. (2.3) равномерное, а, значит, симметричное, обратную функцию можно заменить на:
равномерное, а, значит, симметричное, обратную функцию можно заменить на: . (2.4)
. (2.4) , определенная выражением (2.4) будет иметь экспоненциальное распределение и описывать квадрат длины радиус-вектора.
, определенная выражением (2.4) будет иметь экспоненциальное распределение и описывать квадрат длины радиус-вектора. умножением на
умножением на 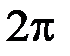 :
: . (2.5)
. (2.5) (2.6)
(2.6) в выражениях (2.6) определяет дисперсию нормально распределенных СВ
в выражениях (2.6) определяет дисперсию нормально распределенных СВ  и
и  . Совместная плотность распределения вероятности для них может быть найдена следующим образом:
. Совместная плотность распределения вероятности для них может быть найдена следующим образом: . (2.7)
. (2.7) – якобиан преобразования.
– якобиан преобразования. и
и 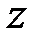 , нетрудно получить:
, нетрудно получить: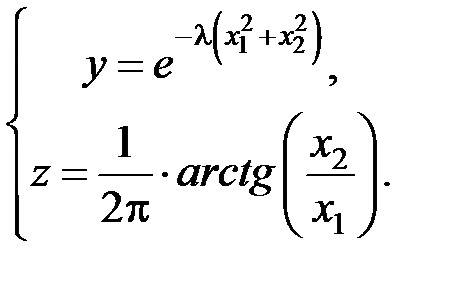 (2.8)
(2.8) . (2.9)
. (2.9) и
и  независимые равномерно распределенные в интервале
независимые равномерно распределенные в интервале  . (2.8)
. (2.8) :
: . (2.9)
. (2.9) :
: . (2.10)
. (2.10) . Выбирая
. Выбирая  , получаем нормированные нормально распределенные СВ, имеющие нулевое математическое ожидание и единичную дисперсию.
, получаем нормированные нормально распределенные СВ, имеющие нулевое математическое ожидание и единичную дисперсию.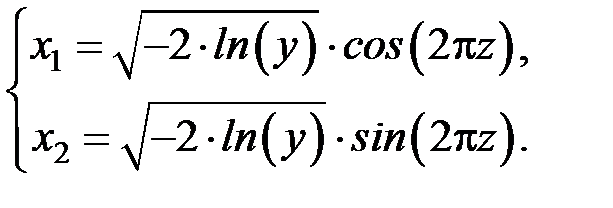 (2.11)
(2.11) и
и  ,
, и
и 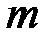 – требуемые значения СКО и математического ожидания, соответственно.
– требуемые значения СКО и математического ожидания, соответственно. и
и 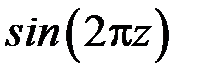 через координаты
через координаты  и длину радиус-вектора
и длину радиус-вектора  :
:
 (2.12)
(2.12) (2.13)
(2.13)