
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Данные контроля, необходимые для построения контрольнойКарты
Здесь введены обозначения: UCL — верхняя граница регулирования; LCL — нижняя граница регулирования; п = 5 — число изделий в выборке; А2 = 0,73, D4 = 2,11, D3 (не определен) — коэффициенты, зависящие от размера выборки п; их значения приведены в табл. 1.2.
Прочерк в столбце D3 табл. 1.2 означает, что контрольный диапазон не имеет нижней границы.  Контрольная карта составляется в следующем порядке: 1. Выполняют измерения 20—25 последовательно изготавливаемых групп изделий, т.е. выборок, по 4—5 изделий в группе (всего не менее 100). 2. Для каждой группы рассчитывают среднее арифметическое где m от — число деталей в группе; где хтin, хтах — наименьшее и наибольшее значение результатов измерений в группе. Таблица 1.2 Коэффициенты для расчета контрольных границ
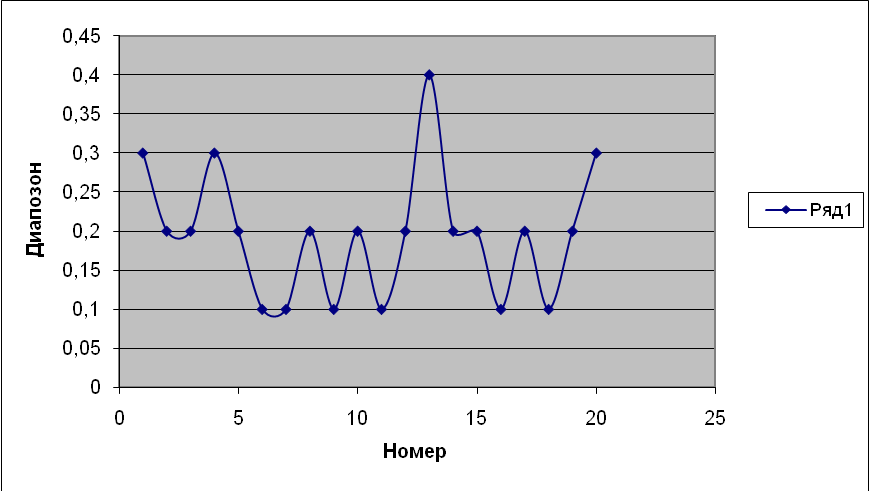
На основе измерений и расчетов могут быть построены контрольные карты, пример которой приведен на рис. 1.1. Когда на карте какая-то точка выходит за контрольную границу – это означает неправильную настройку процесса.
Государственное бюджетное профессиональное образовательное учреждение Астраханской области «Астраханский колледж вычислительной техники»
Специальность 09.02.01
ПРАКТИЧЕСКАЯ РАБОТА №8 Рандомизация результата измерения по дисциплине “Управление качеством”
АКВТ.090201.ПР47.0800
Листов ___
Составил преподаватель /Сботова А.Г./
Рассмотрено на заседании цикловой комиссии специальности 09.02.01
Протокол N от “____”_____________г. и рекомендовано для студентов
Председатель комиссии / Сботова А.Г./
2018 СОДЕРЖАНИЕ
1 Цель работы 3 2 Методические рекомендации 3 3 Порядок выполнения работы 3 4 Содержание отчета 3 5 Контрольные вопросы 3 6 Рекомендуемая литература 3 Приложение. Варианты заданий 4 Приложение. Теоретические сведения 6 1. ЦЕЛЬ РАБОТЫ
1.1. Изучить теоретические сведения 1.2. Получить практические навыки и умения вычисления процедуры рандомизации 2. Методические рекомендации
2.1. Методические указания по выполнению работы
3. Порядок выполнения работы
3.1. Ознакомиться с теоретическими сведениями 3.2. Согласно выбранному варианту решить задачу (см. ПРИЛОЖЕНИЕ А).
4. СОДЕРЖАНИЕ ОТЧЕТА
4.1 Цель работы 4.2 Методические рекомендации 4.3.Порядок выполнения работы 4.4.Ответы на контрольные вопросы 4.5. Выводы
5. КОНТРОЛЬНЫЕ ВОПРОСЫ
5.1. Какие шкалы применяются для измерения? 5.2.Чем обеспечивается правильность результата измерения? 5.3. Что характеризует величина Х и поправка? 5.4. От чего зависит приведенная и относительная погрешность?
6. РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1.Л.Е.Басовский, В.Б.Протасьев «Управление качеством» Москва, 2002
ПРИЛОЖЕНИЕ А ВАРИАНТЫ ЗАДАНИЙ
При метрологической аттестации вольтметра в нормальных условиях выполнено 100 измерений образцового напряжения и различных точках шкалы. Установлено, что распределение вероятности с дисперсией Su2 напряжение равно X В. Смещение средне арифметического значения в сторону меньших значений с вероятностью Y достигает Z В. Необходимо сравнить качество одно кратных и многократных измерений.
Вариант 1: X=2; Y=0,8; Z=+0,42 U=21В Вольтметр дал 6 показаний: 19;19,8;19,5;20;21;20,6;
Вариант 2: X=2,5; Y=0,85; Z=+0,4 U=18В Вольтметр дал 6 показаний: 19;19,8;19,5;20;21;20,6;
Вариант 3: X=2,9; Y=0,95; Z=+0,5 U=25В Вольтметр дал 6 показаний: 19;19,8;19,5;20;21;20,6;
Вариант 4: X=1,8; Y=0,95; Z=+0,25 U=27В Вольтметр дал 6 показаний: 19;19,8;19,5;20;21;20,6;
Вариант 5: X=1,6; Y=0,84; Z=+0,29 U=16В Вольтметр дал 6 показаний: 19;19,8;19,5;20;21;20,6;
Вариант 6: X=2,3; Y=0,9; Z=+0,36 U=20В Вольтметр дал 6 показаний: 19;19,8;19,5;20;21;20,6;
Вариант 7: X=2,9; Y=0,95; Z=+0,25 U=20В Вольтметр дал 6 показаний: 19;19,8;19,5;20;21;20,6;
Вариант 8: X=2; Y=0,9; Z=+0,30 U=30В Вольтметр дал 6 показаний: 19;19,8;19,5;20;21;20,6;
Вариант 9: X=2,8; Y=0,75; Z=+0,5 U=15В Вольтметр дал 6 показаний: 19;19,8;19,5;20;21;20,6;
Вариант 10: X=2,2; Y=0,84; Z=+0,4 U=25В Вольтметр дал 6 показаний: 19;19,8;19,5;20;21;20,6;
ПРИЛОЖЕНИЕ Б ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Напомним, что в соответствии с положениями теоретической метрологии измерение может выполняться с использованием шкалы порядка (уровней), шкалы интервалов и шкалы отношений. Во втором и третьем случаях результат измерения является случайной величиной и может записываться выражением:
где X— показание средства измерения; Величина Х характеризует правильность показаний, а поправка — точность измерений. По этим параметрам измерительная техника разделяется на классы точности в соответствии с допускаемой погрешностью измерений. Приведенная погрешность измеряется в процентах от верхнего предела измерений, относительная погрешность — от результата самого показания. Используется ряд классов точности, в том числе: 0.1, 0.2, 0.5, 1.0, 1.5, 2.5, 4.0. Характеристикой класса является относительная погрешность, указываемая в процентах: 0.1, 0.5, 4.0. Правильность результата измерения обеспечивается совпадением среднего значения измерений со значением измеряемой величины. Значение X — величина случайная, поправка Если значение поправки с течением времени не меняется, то при многократном измерении постоянного размера одним и тем же средством измерений (в одинаковых условиях) получим:
где q — средний арифметический результат измерений; п — количество измерений; X— среднее значение показания при измерении; Это выражение показывает, что точность многократного измерения выше, но правильность такая же, как и при однократном измерении. Пример.При метрологической аттестации вольтметра в нормальных условиях выполнено 100 измерений образцового напряжения и различных точках шкалы. Установлено, что распределение вероятности с дисперсией Su2 напряжение равно 1,5В. Смещение средне арифметического значения в сторону меньших значений с вероятностью 0,95 достигает 0,3В. Необходимо сравнить качество одно кратных и многократных измерений. Решение примера.Из результатов аттестации следует, что в показания вольтметра нужно вносить поправку Стандартная ошибка (среднеквадратичное отклонение) составляет: Su = Если показания вольтметра U = 20В, то результат измерения можно записать в виде: U = (20 + 0,3) ± t x Su = 20,3 ± 2,1 х 1,22 = 20,3 ± 2,56 В. Результат измерения: U= 17,74 ... 22,86 В Точность многократного измерения выше, и соответствующие показатели качества измерения при девяти отсчетах составят:
Допустим, вольтметр дал девять показаний: 20; 21; 20,5; 21; 20,5; 21,5; 20,5; 20,5; 21,2. Тогда Результат измерения можно записать следующим образом: U = (20,74 - 0,3) ± t х 0,406 = 20,44 ± 0,852 В, U= 19,588 ... 21,292.
Погрешность составляет - 4% (
Государственное бюджетное профессиональное образовательное учреждение Астраханской области «Астраханский колледж вычислительной техники»
Специальность 09.02.01
ПРАКТИЧЕСКАЯ РАБОТА №9 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 328. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
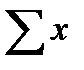
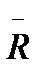 = 0,5x3,9 =0,195 см — половина среднего диапазона (размах);
= 0,5x3,9 =0,195 см — половина среднего диапазона (размах);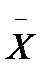 = 5,406 — среди значение размера;
= 5,406 — среди значение размера;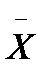 и размах:
и размах: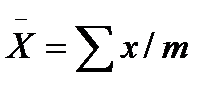 ,
,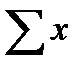 - суммарное значение результатов группы;
- суммарное значение результатов группы;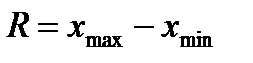 ,
,
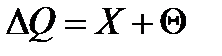
 — поправка.
— поправка.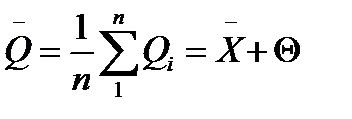
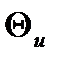 = +0,ЗВ.
= +0,ЗВ.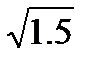 = 1,22В
= 1,22В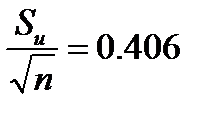
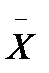 = 20,74.
= 20,74.