
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Тема 2. Законы распределения случайных величин.Литература [2, 3, 4]
Вспомним, что совокупность значений случайных величин, расположенных в возрастающем порядке с указанием их вероятностей, называетсяраспределением случайных величин. При наличии определенных условий распределения случайных величин могут подчиняться вполне определенным законам. Законы распределения случайных величин изучаются в теории вероятностей. Из этих законов наибольшее практическое значение в машиностроении имеют: - для дискретных случайных величин: закон биноминального распределения и закон редких событий; - для непрерывных случайных величин: закон равной вероятности, закон нормального распределения, закон эксцентриситета, закон экспоненциального распределения, закон распределения Вейбулла-Гнеденко, закон логарифмического нормального распределения и закон распределения модуля разности.
1. Закон биноминального распределения.
Закон биноминального распределения используется при оценке качества и надежности изделий. Пусть производится серия последовательных независимых испытаний, каждое из которых заканчивается одним из двух несовместных между собой результатов: или событие A наступает, или оно не наступает. Вероятность появления события A в каждом испытании равна p, а вероятность не появления события A равна q = 1 - p. Так как испытания независимы, то вероятность появления или не появления события A не зависит от результатов предыдущих испытаний. При такой схеме испытаний вероятность появления события A заданное число раз подчиняется закону биномиального распределения, который можно сформулировать так: если вероятность события A постоянна в серии последовательных независимых испытаний и равна p, то вероятность появления события A ровно k раз в п испытаниях будет равна 
где k -число появления события ; n - число независимых испытаний. Это уравнение определяет собой распределение вероятностей случайного числа k, которое называется биномиальным. В формуле (1) символ
где символ n! обозначает факториал и выражает произведение натуральных чисел 1, 2, 3,. . ., n. При этом 0! = 1. С учетом изложенного формула (1) примет вид:
Закон биномиального распределения двухпараметрический, в котором математическое ожидание M(k) и дисперсия
M(k) = np;
Пример 1. В партии деталей имеется брак, доля которого составляет 0,1. Производится последовательное извлечение 10 деталей. После каждого извлечения и обследования детали она вновь возвращается в партию, которая затем тщательно перемешивается, т.е. испытания носят независимый характер. Какова вероятность того, что при извлечении по такой схеме 10 деталей среди них появится одна бракованная? Решение. Очевидно, что вероятность извлечения бракованной детали составляет p = 0,1, вероятность противоположного события - извлечение годной детали q = 1 - p = 0,9. Число испытаний n = 10 и k = 1. Следовательно, по формуле (2) находим
Полученный результат можно отнести и к тому случаю, когда извлекается подряд 10 деталей без возврата их обратно в партию и объем партии достаточно велик. При достаточно большой партии, например 1000 шт., вероятность извлечения годной или негодной детали после каждого из 10 извлечений деталей изменится ничтожно мало. Поэтому при таких условиях извлечение бракованной детали можно рассматривать как событие, не зависящее от результатов предшествующих испытаний.
Пример 2. На участке имеется пять одинаковых станков, коэффициент использования которых по времени составляет 0,8. Какова вероятность того, что в середине смены при нормальном ходе производства из пяти таких станков будет работать только два, а три не работать? Решение. Так как p = 0,8; q = 0,2; n = 5 и k = 2, то
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 350. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (1)
(1) обозначает число сочетаний из n элементов по k, т. е. биномиальный коэффициент. Биномиальный коэффициент вычисляется по формуле
обозначает число сочетаний из n элементов по k, т. е. биномиальный коэффициент. Биномиальный коэффициент вычисляется по формуле ,
, . (2)
. (2) равны:
равны: .
.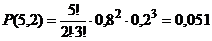 .
.