Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Закон нормального распределения.
Закон нормального распределения находит большое применение в различных отраслях техники. Этому закону подчиняются, многие непрерывные случайные величины, встречающиеся в технике, например ошибки измерения, высота микронеровностей на обработанной поверхности и многие другие. Широкое применение закона нормального распределения в технике находит свое теоретическое обоснование в теореме, которая была доказана выдающимся русским математиком Ляпуновым. Теорема, доказанная Ляпуновым, имеет настолько важное значение в теории вероятностей и ее приложений, что получила название центральной теоремы теории вероятностей. Она объясняет, почему во многих случаях реальные случайные величины с большой точностью следуют закону нормального распределения. Опуская строгую математическую формулировку теоремы Ляпунова и ее доказательства ввиду их сложности, ограничимся лишь описанием следствия из этой теоремы, которое заключается в следующем. Если случайная величина X представляет сумму очень большого числа взаимно независимых случайных величин x1, x2,…, xn, влияние каждой из которых на всю сумму ничтожно мало, то независимо от того, каким законам распределения подчиняются слагаемые x1, x2,…, xn, сама величина X будет иметь распределение вероятностей, близкое к нормальному, и тем точнее, чем больше число слагаемых. Из теоремы Ляпунова можно сделать важный вывод, имеющий большое практическое значение о том, что если изучаемая величина является суммой большого числа независимых случайных слагаемых, то хотя бы последние были нам не известны, часто можно заранее считать, что наша величина имеет нормальное распределение.  Теорема Ляпунова дает теоретическое объяснение и тому факту, что при устойчивом процессе обработки деталей на настроенных станках и при отсутствии изменяющихся во времени систематических погрешностей действительные размеры деталей часто подчиняются закону нормального распределения. Это объясняется тем, что результирующая погрешность обработки представляет собой сумму большого числа погрешностей, зависящих от станка, приспособления, инструмента и заготовки. Плотность вероятности или дифференциальная функция распределения случайной величины непрерывного типа, подчиняющейся закону нормального распределения, имеет следующее выражение:
где x - переменная случайная величина; φ(x)- плотность вероятности; σ- среднее квадратическое отклонение случайной величины x от
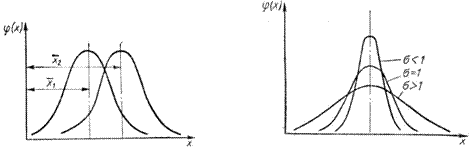
e- основание натуральных логарифмов, e = 2,71828. Дифференциальная функция нормального распределения графически выражается в виде кривой холмообразного типа (рис. 1). Из вида кривой нормального распределения следует, что она симметрична относительно ординаты точки x =
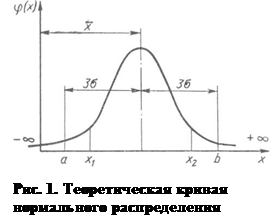
Положение кривой относительно начала координат и ее форма определяются двумя параметрами Интегральная функция закона нормального распределения описывается уравнением
график которого приведен на рис 4.
Вероятность P(-∞ < x < ∞) = 1 представляет собой площадь под дифференциальной кривой нормального распределения. Очевидно, что вероятность значений x в любом другом интервале x1 – x2 (см. рис. 1) меньше единицы и будет равна
Произведем замену переменной x путем подстановки
Новые пределы интегрирования
Знак плюс в уравнении (11) изменился на минус вследствие изменения пределов интегрирования. Интеграл
Таким образом, вероятность того, что случайная величина, подчиняющаяся закону нормального распределения, при испытаниях примет значение в пределах x1 – x2, может быть записана через Φ(t) следующим образом:
У теоретической кривой нормального распределения ветви ее асимптотически приближаются к оси абсцисс и встречаются с последней где-то в бесконечности, т. е. зона рассеивания случайной величины x лежит в пределах ±∞. При практическом использовании закона нормального распределения зону рассеивания случайной величины x ограничивают конечными пределами. В технике и многих других прикладных науках считают, что практическая зона рассеивания случайной величины x, подчиняющейся закону нормального распределения, лежит в пределах Нетрудно убедиться в том, что значения случайной величины x будут лежать в интервале от
так как
Следовательно,
Согласно данным таблицы П.1 приложения 2Ф(3) = 0,9973. Таким образом, вероятность q появления случайной величины вне указанного интервала не превосходит q = 1 - p = 1 - 0,9973 = 0,0027, т. е. очень мала. Поэтому в технике принято зону рассеивания случайной величины x, подчиняющейся нормальному распределению, ограничивать трехсигмовыми пределами. Если
Вводя замену
Так как
поэтому
Закон равной вероятности.
Если непрерывная случайная величина x при испытаниях принимает все значения интервала (a, b) с одинаковой плотностью вероятности, то распределение плотности вероятности графически будет выражаться в виде прямоугольника с основанием ab и высотой φ(x) = const (рис. 6). Такой закон распределения непрерывной случайной величины называется законом равной вероятности, а само распределение — равномерным.
При интервале изменений случайной величины x от a до b:
т. е. вероятность того, что случайная величина х при испытаниях будет принимать значения в интервале от a до b, равна площади под дифференциальной кривой распределения. В соответствии с рис. 6 эта площадь представляет собой прямоугольник с основанием ab и высотой φ(x), следовательно,
Отсюда уравнение дифференциальной функции распределения или плотности вероятности будет иметь следующий вид:
Закон равной вероятности имеет два параметра: M(x) »
откуда
Интегральная функция равномерного распределения выражается следующим уравнением для (a < x < b):
Если x < a, то F(x) = 0; если x ≥ b, то F(x) = 1. Когда a = -b, M(x) = 0, то
График интегральной функции распределения приведен на рис. 7. Законом равной вероятности описывается распределение показателей точности обработки, на величину которых оказывает влияние доминирующий фактор, изменяющийся во времени (износ инструмента, изменение температуры и т. п.).
|
||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 341. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
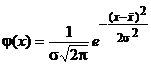 , (7)
, (7)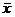 ;
;
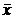 на положение кривой распределения относительно начала координат
на положение кривой распределения относительно начала координат
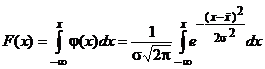 , (8)
, (8)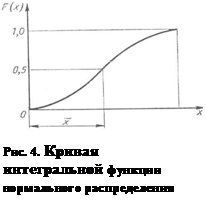 Если случайная величина x следует нормальному закону, то достоверно, что она может принимать любые численные значения в пределах ±∞, поэтому
Если случайная величина x следует нормальному закону, то достоверно, что она может принимать любые численные значения в пределах ±∞, поэтому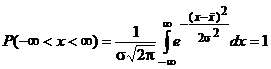 . (9)
. (9)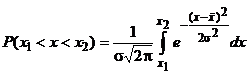 .
.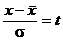 и, учитывая, что
и, учитывая, что 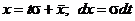 , получим
, получим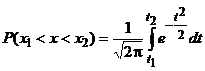 . (10)
. (10)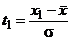 и
и 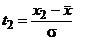 заменили пределы x1 и x2. Правую часть уравнения (10) можно представить в виде суммы двух интегралов:
заменили пределы x1 и x2. Правую часть уравнения (10) можно представить в виде суммы двух интегралов: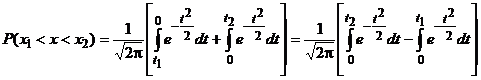 . (11)
. (11)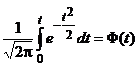 носит название нормированной функции Лапласа и его значения для различных
носит название нормированной функции Лапласа и его значения для различных 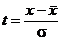 приведены в табл. П.1 приложения. Эта функция нечетная, следовательно, Φ(-t) = - Φ(t) и для отрицательных значений t табличные данные берутся со знаком минус. В табл. П.1 приложения приведены также удвоенные значения функции, т. е.
приведены в табл. П.1 приложения. Эта функция нечетная, следовательно, Φ(-t) = - Φ(t) и для отрицательных значений t табличные данные берутся со знаком минус. В табл. П.1 приложения приведены также удвоенные значения функции, т. е.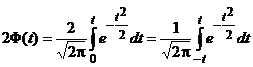 .
.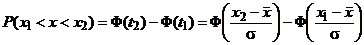 .
.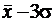 до
до 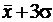 с вероятностью, весьма близкой к единице. Действительно, в этом случае
с вероятностью, весьма близкой к единице. Действительно, в этом случае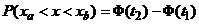 ,
,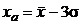 ;
; 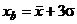 , а
, а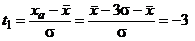 ;
; 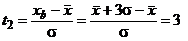 .
.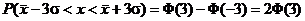 .
.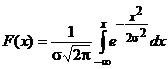 .
.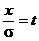 , получим
, получим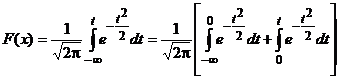 .
.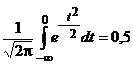 , а
, а 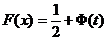 (12)
(12)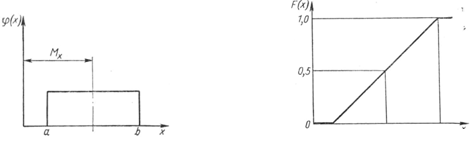
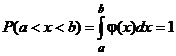 ,
,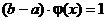 .
.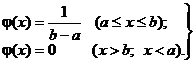 (15)
(15)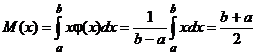 ; (16)
; (16)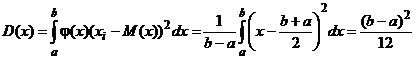 , (17)
, (17)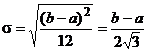 . (18)
. (18)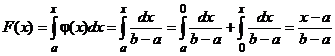 , (19)
, (19)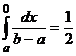 и для этого случая уравнение (19) примет вид
и для этого случая уравнение (19) примет вид