
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Закон распределения модуля разности.
Если две случайные величины x1 и x2 каждая в отдельности имеют нормальное распределение с параметрами
имеет распределение, которое носит название закона распределения модуля разности. Этому закону распределения, например, подчиняются погрешности взаимно расположенных поверхностей и осей, а также погрешности формы деталей: овальность, конусность. Плотность вероятности (дифференциальная функция) распределения случайной величины r выражается следующим уравнением:
где Интегральная функция распределения модуля разности r выражается следующим уравнением:
Произведя замену переменных в уравнениях (22) и (23):
получим следующие выражения:
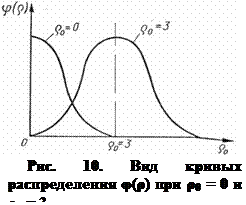
Вид кривой распределения φ(ρ) зависит от значения ρ0. При ρ0 = 0 кривая резко асимметрична, при ρ0 = 3 она совпадает с кривой нормального распределения (рис. 10). Если обозначить
так как каждое слагаемое уравнения (25) является функцией Лапласа
Среднее значение  3ная ρ0 и σρ, можно определить параметры распределения σ0 и
Пользуясь формулой (26) и известными из опыта значениями Пусть, например, в большой выборке из партии втулок среднее значение овальности равно Определим по формуле (27)
Этому значению λ0 по табл. П.2 приложения соответствует ρ0 = 1,12, а по табл. П.3 приложения для ρ0 = 1,12 путем интерполяции имеем σρ = 0,829. По формуле (28) определяем σ0:
Так как в формуле (26)
Подставляя значение ρ и σ0 в формулу (26), получим
По табл. П1 приложения Ф(0,93) = 0,3238 и Ф(3,17) = 0,4992. Следовательно, F(ρ) = 0,3238 + 0,4992 = 0,8230 и вероятный процент годных деталей в партии составит 82,3%, а вероятный процент брака: 100% - 82,3% = 17,7%.
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 440. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
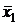 и
и 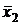 и
и 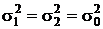 , то модуль разности этих величин
, то модуль разности этих величин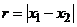
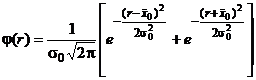 , (22)
, (22)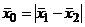 и σ0 являются параметрами распределения модуля разности r.
и σ0 являются параметрами распределения модуля разности r.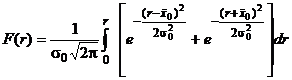 . (23)
. (23)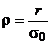 ,
, 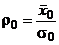 ,
, 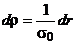 ,
,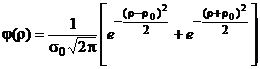 ; (24)
; (24)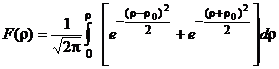 . (25)
. (25)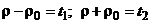 , то уравнение (25) можно заменить следующим уравнением:
, то уравнение (25) можно заменить следующим уравнением: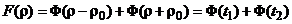 , (26)
, (26)
 Между σr,
Между σr, 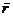 и ρ0 существует определенная зависимость, которая определяется через нормированное
и ρ0 существует определенная зависимость, которая определяется через нормированное 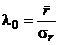 . (27)
. (27)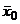 по следующим формулам:
по следующим формулам: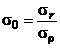 ; (28)
; (28)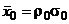 . (29)
. (29)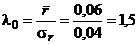 .
.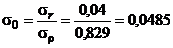 .
.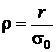 , а допускаемое r = 0,1, то
, а допускаемое r = 0,1, то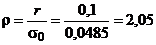 .
.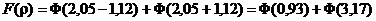 .
.