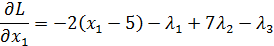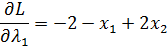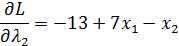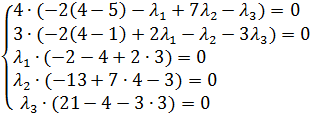Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Решение задач выпуклого программирования⇐ ПредыдущаяСтр 13 из 13 Рассмотрим задачу НП: Z = f(x1,…, xn)®min (max); gi(x1,…, xn) ≤bi, xi ≥ 0, Функция f называется выпуклойна выпуклом множестве Х, если для любой пары точек x,y f(αx + (1 – α) y) ≤ αf(x) + (1 – α) f(y). Функция f называется вогнутой на выпуклом множестве Х, если для любой пары точек x,y f(αx + (1 – α) y) ≥ αf(x) + (1 – α) f(y). Функция f называется строго выпуклой (строго вогнутой), если неравенства в соотношениях являются строгим для всех x ≠ y, т.е. знак неравенства "<" (соответственно, ">"). Очевидно, что если f — выпуклая функция, то g = -f — вогнутая функция. Сумма выпуклых (вогнутых) функций — выпуклая (вогнутая) функция. Линейная функция является как выпуклой, так и вогнутой функцией. Простейший пример выпуклой функции: z = х2, а вогнутой: z = Множество допустимых решений задачи НП удовлетворяет условию регулярности, если существует, по крайней мере, одна точка Xiиз ОДРтакая, что gi(Xi)<bi. Задача НП является задачей выпуклого программирования, если она удовлетворяет следующим условиям: 1) целевая функция f – выпукла (вогнута); 2) все функции gi в ограниченияхвыпуклые. Легко проверить, что если g — выпуклая (вогнутая) функция, то для любого числа b множество {х | g(x) ≤ (≥) b} — выпуклое. Поэтому ОДР в задаче выпуклого программирования - выпуклое множество. Выпуклым будет и множество оптимальных решений. Если же ЦФ— строго выпуклая (вогнутая) функция, то множество точек ее минимума (максимума) состоит из единственной точки.  Наиболее важное свойство таких задач: любая точка локального оптимума задачи выпуклого программирования является точкой ее глобального оптимума. Поэтому, в задаче выпуклого программирования можно говорить об оптимальном решении, не уточняя, идет речь о глобальном или локальном оптимуме. Составим функцию Лагранжа для задачи выпуклого программирования: L(x, λ) = L(x1,…, xn, λ 1,…, λm) = f(x1,…, xn) + Точка Теорема Куна-Таккера Для задачи выпуклого программирования множество допустимых решений, удовлетворяющее условиям регулярности, Если предположить, что функции f и giнепрерывно дифференцируемы, то можно записать условия Куна-Таккера, определяющие необходимые и достаточные условия того, чтобы точка
Предпоследнее условие означает, что если множитель Лагранжа положителен, то соответствующее ему ограничение в точке оптимума обязательно должно быть равенством. Если же ограничение не является равенством в точке оптимума, то его множитель Лагранжа равен нулю. Это условие аналогично условию дополняющей нежесткости в задачелинейного программирования. В отличие от классической задачи условной оптимизации на множители Лагранжа накладывается условие неотрицательности. Множители Лагранжа допускают интерпретацию, аналогичную интерпретации оптимальных оценок ограничений в задаче линейного программирования. Так множитель Лагранжа i-го ограничения характеризует величину изменения оптимального значения целевой функции при увеличении правой части этого ограничения на единицу и фиксированных значениях остальных ограничений. Однако в отличие от задачи линейного программирования величина Пример 2 Решить задачу выпуклого программирования средствами MSExcel.
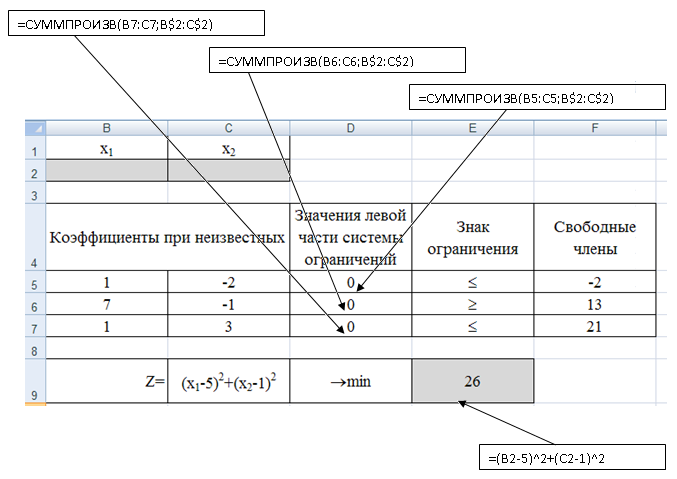
Проверить выполнение условий Куна-Таккера для найденной оптимальной точки. Решим задачу с использованием настройкиПоиск решения.Для решения нашей задачи создадим в Excelкнигу с именем «Решение задачи нелинейного программирования». Подготовим данные на листе. Сначала определим ячейки, в которые будет помещен результат решения. Пусть это будут ячейки В2, С2, сделаем у них заголовки. В этих ячейках нет данных, их должен будет рассчитать Excel, они выделены цветом. Далее заполним коэффициенты при неизвестных и правые части системы ограничений (строки 5-7). Заведем строку 9 для целевой функции. Цветом выделена ячейка, в которой будет находиться значение целевой функции для найденного оптимального решения.
В ячейки D5, D6, D7 ведем формулы для зависимостей левых частей системы ограничений, а в ячейку E9 – формулу для зависимости целевой функции.
Далее необходимо воспользоваться надстройкой Поиск решения. На вкладке Данные в группе Анализ выберитекомандуПоиск решения. Появится диалоговое окно Поиск решения, которое необходимо заполнить следующим образом (для добавления ограничений пользуемся кнопкой Добавить):
Далее нажимаем кнопку Параметры и в появившемся окне Параметры поиска решений устанавливаем флажок неотрицательные значения и нажимаем OK.
В окне Поиск решения после нажатия кнопкиВыполнить появляется окно Результаты поиска решения, в котором выбираем сохранение найденных значений и нажимаем кнопку ОК.
Результаты поиска решений (для ячеек В2 и С2 установлены числовые форматы с 0 знаками после запятой):
Получили Покажем, что существует Перепишем задачу в виде:
Составим функцию Лагранжа
Найдем частные производные:
Запишем условия Куна-Таккера:
Подставим в систему координаты оптимальной точки (4;3), найденной средствами Excel.
Произведение равно нулю, если один из множителей равен нулю. Из первого и второго уравнений следует, что выражения в скобках равны нулю. Из четвертого и пятого уравнений следует, что l2=l3=0. Подставим их в остальные уравнения.
Откуда, находим решение: l1=2, l2=0, l3=0. Следовательно, точка(4;3) является точкой экстремума. Вопросы для самопроверки 1. В чем отличие НП от задачиЗЛП? 2. В чем особенности нахождения решения задач НП? 3. Для каких задач НП разработаны методы решения? 4. В чем особенности графического решения задачи НП? 5. Какая функция называется функцией Лагранжа? Какой смысл множителей Лагранжа? 6. Сформулируйте условия Куна-Таккера. 7. Какие особенности имеет решение задачи выпуклого программирования? Литература 1. Акулич И.Л. Математическое программирование в примерах и задачах. - М.: Высшая школа, 1986 2. Интрилигатор М. Математические методы оптимизации и экономическая теория. М.: Айрис-Пресс, 2002. 3. Исследование операций в экономике/ Под ред. Н.Ш. Кремера. - М.:, ЮНИТИ, 2005 4. Конюховский П. В. Математические методы исследования операций в экономике - СПб: Питер, 2000 5. Косоруков О.А,, Мищенко А.В. Исследование операций - М: Экзамен, 2003 6. Кузнецов А.В., Сакович В.А., Холод Н.И. Высшая математика. Математическое программирование. - Минск: Вышэйшая школа, 1994 7. Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. Математическое программирование. — М.: Высшая школа, 1986 8. Эддоус М., Стэжфилд Р. Методы принятия решений – М.: Аудит, ЮНИТИ, 1997 9. Шикин Е. В., Шикина Г. Е. Исследование операций :. - М. : ТК Велби, Проспект, 2006 |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 370. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
.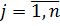
 Х и любого числа α
Х и любого числа α  (0, 1) справедливо соотношение
(0, 1) справедливо соотношение .
. λi(bi– gi(x1,…, xn)).
λi(bi– gi(x1,…, xn)).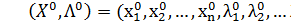 называется седловой точкой функции Лагранжа, если выполняется
называется седловой точкой функции Лагранжа, если выполняется  .
. является оптимальным планом тогда и только тогда, если существует
является оптимальным планом тогда и только тогда, если существует 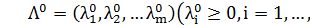 , что
, что  - седловая точка функции Лагранжа.
- седловая точка функции Лагранжа.
 не равна в точности изменению оптимального значения целевой функции при увеличении правой части i-го ограничения на единицу, а дает лишь приближенную оценку этого изменения.
не равна в точности изменению оптимального значения целевой функции при увеличении правой части i-го ограничения на единицу, а дает лишь приближенную оценку этого изменения.






 .
.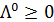 , при которой в точке минимума выполняются условия Куна-Таккера .
, при которой в точке минимума выполняются условия Куна-Таккера .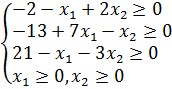

 . Для данной задачи она имеет вид:
. Для данной задачи она имеет вид: