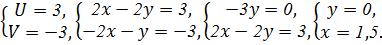Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Критерий недостаточного основания ЛапласаНаходим среднее значение элементов каждой строкипо формуле
Найденные значения заносим в соответствующий столбец и выбираем максимальное Максиминный критерий Вальда В каждой строке находим минимальный элемент: Критерий минимаксного риска Сэвиджа Рассчитаем матрицу рисков. В каждом столбце находим максимальный элементbj.
Заполним матрицу рисков по столбцам. Для этого вычитаем из bj все остальные элементы столбца, результаты записываем на соответствующих местах (в каждом столбце на месте максимального будет 0).
В каждой строке матрицы рисков находим максимальный элемент: Критерий пессимизма-оптимизма Гурвица Для каждой строки рассчитываем значение критерия по формуле:
Выбираем максимальное Ответ: 1) Стратегия А1 является оптимальнойсогласно критерию пессимизма-оптимизма Гурвица.  2) Стратегии А2, А4 не являются оптимальными ни по одному из критериев. 3) Стратегия А3 является оптимальной согласно пессимистическим критериям Вальда и Сэвиджа. 4) Стратегия А5 является оптимальной согласно критерию Лапласа. Вопросы для самопроверки 1. Сформулируйте постановку задачи о назначениях с минимизацией, максимизацией функции? В чем отличия вих решениях? 2. В чем заключается алгоритм венгерского метода решения задачи о назначениях? 3. Что такое стратегия игрока? Какая игра называется парной с нулевой суммой? 4. Что такое платежная матрица? 5. Как определить верхнюю и нижнюю цену игры? Каково соотношение между ними? 6. Какая игра имеет седловую точку? Что означает решение игры в чистых стратегиях? 7. Что такое оптимальная смешанная стратегия? 8. Сформулируйте основную теорему теории игр – теорему Фон-Неймана. 9. Как можно графически решить игру? 10. На чем основана связь матричной игры и ЗЛП? 11. В чем отличие игр с природой? 12. Перечислите основные критерии решения игр с природой. Многоцелевые задачи Задачи, решаемые с учетом множества показателей или критериев, носят название многоцелевых. При решении таких задач найти такой план, при котором система критериев была бы наилучшей. Если все критерии равнозначны, то эффективным считается такой план, при котором отклонения от оптимумов по каждому критерию равны. С привычной точки зрения задача со многими критериями решения не имеет - далеко не всегда есть возможность одновременного удовлетворения всех заданных условий. Поэтому, когда говорят о решении многокритериальной задачи, имеют в виду какой-нибудь компромисс между изначально противоречивыми требованиями. А так как практически любая подобная ситуация допускает разные компромиссные разрешения, то и подходы к их поиску многочисленны и весьма разнообразны. Перечислим некоторые подходы. Метод уступок- лицо, принимающее решения, подводится к выбору решения путем постепенного ослабления первоначальных требований, как правило, одновременно невыполнимых. Метод идеальной точки- в области допустимых значений неизвестных ищется такая их совокупность, которая способна обеспечить набор значений критериев, в том или ином смысле ближайший к наилучшему, как правило, недосягаемому (в так называемой точке утопии). Метод свертывания- лицо, принимающее решения,сводит многокритериальную задачу к задаче с одним критерием. Метод ограничений- множество допустимых значений неизвестных уменьшается путем осмысленного введения дополнительных ограничений на заданные критерии. Метод анализа иерархий- на основании суждений экспертов оценивается вклад в общую оценку каждого критерия. Далее будем рассматривать случаи, когда решение принимается по двум критериям. Множество Парето Рассмотрим на плоскости (U, V) произвольное множество W. Каждая точка плоскости обладает одним из следующих трех свойств: либо все точки, ближайшие к ней, принадлежат множеству W (такая точка называется внутренней точкой множества W), либо все точки, ближайшие к ней, множеству W не принадлежат (такая точка называется внешней точкой по отношению к множеству W), либо сколь угодно близко от нее расположены как точки множества W, так и точки, множеству W не принадлежащие (такие точки называются граничными точками множества W). Множество всех граничных точек множества называется его границей. Точки множества W можно разбить на три класса: -к первому классу относятся точки, которые, оставаясь во множестве W, можно сдвинуть так, чтобы одновременно увеличились обе координаты (в этот класс попадают все внутренние точки множества W и часть его граничных точек); -второй класс образуют граничные точки, перемещением которых по границе Wможно увеличить только одну из координат при сохранении значения второй (вертикальный отрезок АВ и горизонтальный отрезок CD на границе множества W); -в третий класс попадут граничные точки, перемещение которых по границеWуменьшает одну из координат при одновременном увеличении другой (дуга BD границы W).
Множество точек третьего класса принято называть границей (множеством) Парето данного множества W. Приведем примеры границы Парето некоторых простейших множеств.
Другими словами, в множество Парето не включаются такие решения, которые могут быть улучшены одновременно по обоим критериям. Укажем простое геометрическое правило, посредством которого можно выделять из заданного плоского множества его границу Парето.
Метод идеальной точки Рассмотрим постановку двухкритериальной задачи в общем виде: Пусть на плоскости (х,y) задано множество ω и в каждой точке этого множества определены две непрерывные функции: U = Φ(x,y) и V = Ψ(x,y).
Метод идеальной точки использует множество Парето, составленное из допустимых точек задачи, которые не могут быть «сдвинуты» в пределах допустимого множества с улучшением сразу по обоим критериям.На границе Парето отыскиваются точки, ближайшие к точке утопииP(точка утопии дает сочетание наилучших значений всех критериев, но обычно не удовлетворяет заданным ограничениям). Рассмотрим реализацию метода идеальной точки на конкретном примере. Пример Решить двухкритериальную задачу линейного программирования методом идеальной точки.
Решение 1. Построим область допустимых решений в плоскости xOy, определяемую системой неравенств. Каждое линейное неравенство на плоскости задает полуплоскость, все точки которой обращают неравенство в верное числовое неравенство. Рассмотрим первое неравенство 4y – x ≤ 20. Границей полуплоскости является прямая 4y – x = 20. Построим эту прямую по двум точкам. Составим таблицу:
Определим, какую полуплоскость задает первое неравенство: выше построенной прямой или ниже ее. Для этого подставим в неравенство координаты любой «пробной» точки, не лежащей на построенной прямой. Возьмем в качестве «пробной точки» начало координат: (0; 0):
Получили верное числовое неравенство, значит рассматриваемое линейное неравенство определяет полуплоскость, которой принадлежит начало координат, т.е. расположенную ниже построенной прямой. Отметим выбранную полуплоскость. Аналогично определим полуплоскости, задаваемые вторым и третьим неравенствами: 4x + y ≤ 22 и х – у ≤ 3.
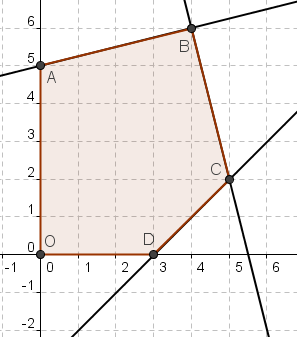
Оставшиеся ограничения: х ≥ 0, у ≥ 0 задают первую координатную четверть. Область допустимых решений – многоугольник OABCD.
2. Построим в критериальной плоскости область, соответствующую области допустимых решений OABCD. Для этого необходимо найти координаты вершин. В нашем случае, очевидно, что O(0; 0), A(0; 5), B(4; 6), C(5; 2), D(3; 0), т.к. часть этих точек использовалась при построении прямых. В общем случае координаты точки пересечения двух прямых определяют совместным решением их уравнений, например, для точки С, которая является точкой пересечения (2) и (3) прямых необходимо решить систему:
Сложим уравнения, получим: Найдем координаты образов точек O, A, B, C, D в линейном преобразовании, определяемом целевыми функциями: O(0; 0): Таким образом, O(0; 0) → O¢(0; 0). A(0; 5): Таким образом, A(0; 5) → A¢(–10; –5). B(4; 6): Таким образом, B(4; 6) → B¢(–4; –14). C(5; 2): Таким образом, C(5; 2) → C¢(6; –12). D(3; 0):
Таким образом, D(3; 0) → D¢(6; –6). По найденным координатам точек построим в критериальной плоскости UOV образ многоугольника OABCD – многоугольник O¢A¢B¢C¢D¢.
3. В критериальной плоскости найдем границу Парето – северо-восточную границу области O¢A¢B¢C¢D¢.
Точкой утопии, в которой достигается максимум одновременно по двум критериям U и V, является точка P: через самую высокую (северную) точку области O¢A¢B¢C¢D¢ провели горизонтальную прямую (через точку O¢) и через самую правую (восточную) точку области O¢A¢B¢C¢D¢ провели вертикальную прямую (через точкиC¢ и D¢); точка – точка пересечения горизонтальной и вертикальной прямой.
4. На границе Парето найдем идеальную точку – точку, наиболее близко расположенную к точке утопии. В нашем случае это основание перпендикуляра, опущенного из точки утопии Р на отрезок O¢D¢ – точка M¢
Найдем координаты точки M¢. Для этого найдем уравнение прямой O¢D¢. Воспользуемся уравнением прямой, проходящей через две точки:¢(0; 0),
Найдем уравнение перпендикуляра, опущенного из точки утопии P на отрезок O¢D¢. Воспользуемся уравнением прямой с точкой и вектором нормали:
Координаты точки М¢: Сложим уравнения: Таким образом, М¢(3; –3), а значит, компромиссное решение позволит достигнуть значений целевых функций: U = 3, V = –3. 5. Найдем координаты точки в плоскости xOy, которой соответствует точка М¢ критериальной плоскости. Для этого решим систему уравнений:
Получили, что компромиссным решением метода идеальной точки является M(1,5; 0), в которой критерии достигают значений U = 3, V = –3.
Ответ:M(1,5; 0), Umax (1,5; 0)= 3, V max(1,5; 0)= –3. Вопросы для самопроверки 1. Какая задача называется многоцелевой? 2. Каким своством обладают точки множества Парето? 3. Как найти множество Парето? 4. Что такое точка утопии? 5. В чем суть метода идеальной точки? Какая точка называется идеальной? |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 413. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |





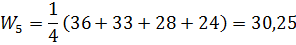
 , значит оптимальной по данному критерию является стратегия А5.
, значит оптимальной по данному критерию является стратегия А5.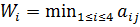 и выбираем максимальное
и выбираем максимальное  , значит оптимальной по данному критерию является стратегия А3.
, значит оптимальной по данному критерию является стратегия А3. и выбираем минимальное значение
и выбираем минимальное значение 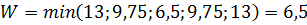 , значит, оптимальной по данному критерию является стратегия А3.
, значит, оптимальной по данному критерию является стратегия А3. . По условию l=0,4.
. По условию l=0,4.






 , значит оптимальной по данному критерию является стратегия А1.
, значит оптимальной по данному критерию является стратегия А1.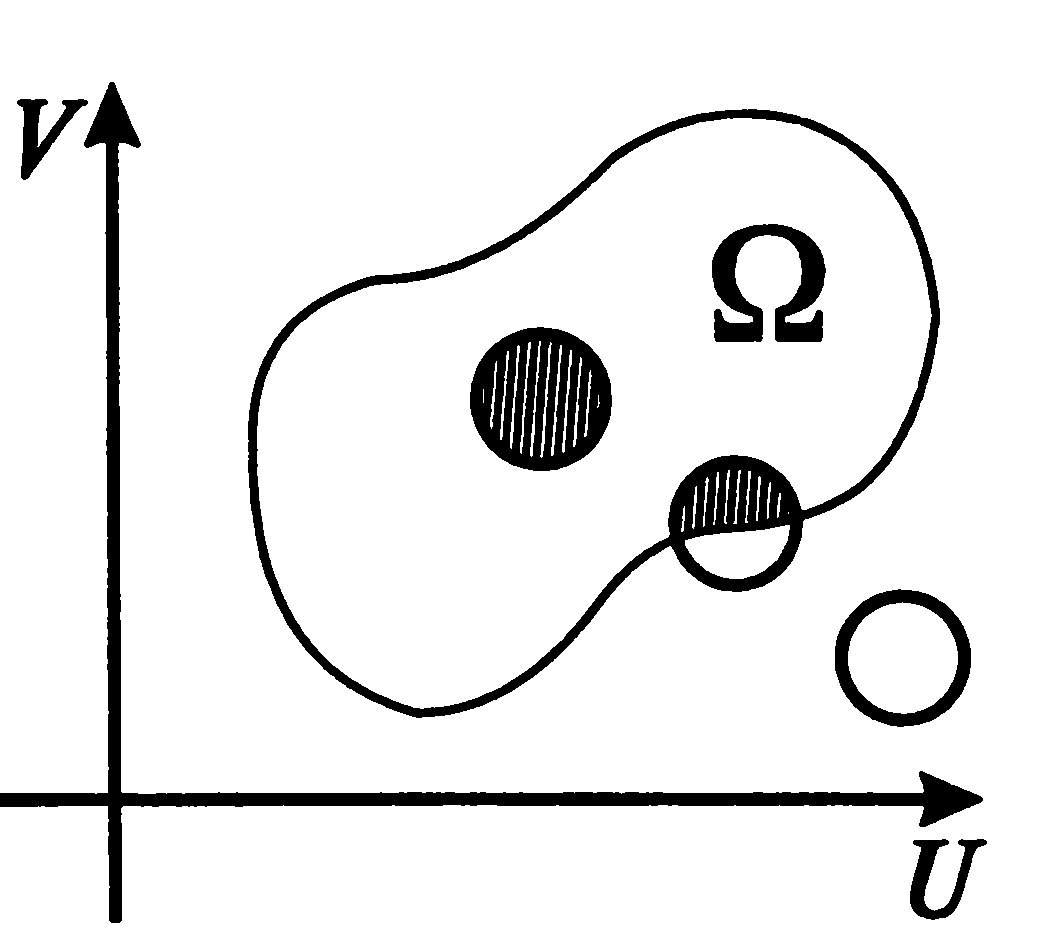

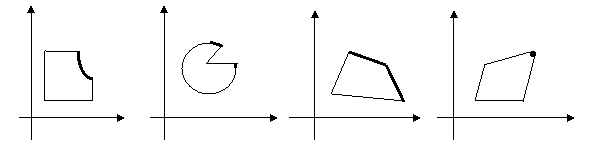 Говоря нестрого, граница Парето множества W- это точки, из которых нельзя сдвинуться на "север", "восток" либо "северо-восток", оставаясь в том же множестве W.
Говоря нестрого, граница Парето множества W- это точки, из которых нельзя сдвинуться на "север", "восток" либо "северо-восток", оставаясь в том же множестве W. Рассмотрим пробный прямой угол, стороны которого сонаправлены координатным осям U и V.Положение этого пробного угла на плоскости однозначно определяется его вершиной Q. Перемещая пробный угол (параллельно самому себе), мы будем собирать только те точки заданного множества W, которые можно совместить с точкой Q так, чтобы ни одна другая точка множества W не попадала ни внутрь этого угла, ни на одну из его сторон. Совокупность всех таких точек и будет искомой границей Парето для множества W.
Рассмотрим пробный прямой угол, стороны которого сонаправлены координатным осям U и V.Положение этого пробного угла на плоскости однозначно определяется его вершиной Q. Перемещая пробный угол (параллельно самому себе), мы будем собирать только те точки заданного множества W, которые можно совместить с точкой Q так, чтобы ни одна другая точка множества W не попадала ни внутрь этого угла, ни на одну из его сторон. Совокупность всех таких точек и будет искомой границей Парето для множества W.
 Сразу же отметим, что в общем случае поставленная задача решения не имеет. В самом деле, изобразим на плоскости (U,V)все точки, координаты которых вычисляются по формуламU = Φ(x,y) и V = Ψ(x,y). Обозначим полученное множество через W. Из рисунка видно, что Umax (наибольшее значение U)и Vmax (наибольшее значение V)достигаются в разных точках, а точка P с координатами (Umax, Vmax) лежит вне множества W. Таким образом, в исходной постановке задача, вообще говоря, неразрешима - удовлетворить обоим требованиями одновременно невозможно. И, следовательно, нужно искать какое-то компромиссное решение.
Сразу же отметим, что в общем случае поставленная задача решения не имеет. В самом деле, изобразим на плоскости (U,V)все точки, координаты которых вычисляются по формуламU = Φ(x,y) и V = Ψ(x,y). Обозначим полученное множество через W. Из рисунка видно, что Umax (наибольшее значение U)и Vmax (наибольшее значение V)достигаются в разных точках, а точка P с координатами (Umax, Vmax) лежит вне множества W. Таким образом, в исходной постановке задача, вообще говоря, неразрешима - удовлетворить обоим требованиями одновременно невозможно. И, следовательно, нужно искать какое-то компромиссное решение.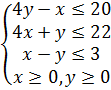







 . Откуда
. Откуда 

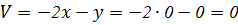





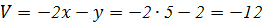

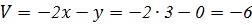






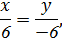

 ,
, 
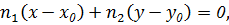



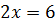 . Решение уравнения
. Решение уравнения