
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Решение матричных игр 2х2 в смешанных стратегияхИгра 2х2 – наиболее простой случай конечных игр. Рассмотрим игру, не имеющую седловой точки, с платежной матрицей
Пусть
Решаем систему
Аналогично, составляем систему для игрока В:
Решая систему, находим:
Цена игры
Решение игры 2х2 можно найти так же геометрически. Для этого на оси абсцисс отложим отрезок А1А2 длиной 1. Левый конец отрезка (p=0) соответствует стратегии А1, правый – стратегии А2. Промежуточные точки отрезка соответствуют смешанным стратегиям 
Аналогично можно рассмотреть задачу минимизации верхней границы выигрыша для игрока В. Используя геометрическую интерпретацию можно найти решение игр, заданных матрицей 2хn. Каждой из nстратегий игрока В будет соответствовать прямая. Точка N, лежащая на нижней границе и дающая наибольшую величину выигрыша, определяет цену игры и ее решение. При этом определяются активные стратегии игрока В (соответствующие им прямые пересекаются в точке N). Для активных стратегий вероятности не равны 0, остальные стратегии игроком В не используются (их вероятности равны 0). Аналогично можно решить игру с матрицей mxn. В этом случае строят верхнюю границу выигрыша и на ней определяют минимум. Пример 4 Игра задана платежной матрицей 1) Решить игру аналитически. 2) Провести моделирование результатов игры с помощью таблицы равномерно распределенных случайных чисел, разыграв 30 партий; определить относительные частоты использования чистых стратегий каждым игроком и средний выигрыш, сравнив результаты с полученными теоретически в п.1. Решение: 1.Найдем нижнюю и верхнюю цену игры.
a¹b, следовательно, игра не имеет седловой точки, решение будет в смешанных стратегиях. Найдем аналитически оптимальную стратегию игрока А Так как для стратегии В1: для стратегии В2: С учетом того, что сумма вероятностей смешанной стратегии равна 1, получаем систему уравнений: Вычтем из первого уравнения второе: Итак: Аналогично получаем систему для нахождения смешанной стратегии игрока В. Вычтем из первого уравнения второе:
Итак: Ответ: 2. Проведем моделирование результатов решения с помощью таблицы равномерно распределенных случайных чисел. Для 30 партий хватит 60 чисел, на основе которых будут выбираться стратегии игроками. Используемые случайные числа сгенерированы в MSExcel функцией =СЛЧИС(). В приложении достаточно много чисел, но использовать для моделирования можно любые 60, выбранные произвольно с любого места таблицы. Выберем 60 чисел:
Будем выбирать стратегии игроков, используя геометрическое определение вероятности. Так как все случайные числа из отрезка [0; 1], то чтобы стратегия А1 появлялась примерно в половине случаев, будем ее выбирать если случайное число меньше 0,5; в остальных случаях выбирается стратегия А2. Аналогично для игрока В. Стратегию В1 будем выбирать, если соответствующее случайное число меньше 2/3»0,67, в противном случае выбираем стратегию В2. Заполним расчетную таблицу (Средний выигрыш игрока А считаем, как отношение накопленного выигрыша к количеству сыгранных партий):
Таким образом, в результате моделирования в 30 партиях цена игры (средний выигрыш) равен 9,2. Этот результат согласуется с теоретической ценой игры 9. Из 30 партий игрок А 18 раз применял стратегию А1, 12 раз – стратегию А2. Игрок В 21 раз применял стратегию В1, 9 раз – стратегию В2.Частоты использования игроками своих чистых стратегий соответственно равны: `p=(18/30;12/30)=(0,6;0,4),`q=(21/30;9/30)=(0,7;0,3). Сравнивая с теоретическими оптимальными стратегиями Пример 5 Решить графически игру, заданную платежной матрицей Решение Матрица игры имеет размер 2х3, поэтому решение игры будем искать для игрока А. Отложим отрезок единичной длины А1А2, каждой точке которого поставим в соответствие некоторую смешанную стратегию первого игрока – (p1, p2). В частности, точке А1соответствуетстратегия А1, точке А2 – стратегия А2. В точках А1 и А2 восстановим перпендикуляр и на полученных прямых будем откладывать выигрыши игрока А при соответствующих стратегиях и строить прямые, соответствующие стратегиям игрока В.
В соответствии с принципом минимакса ломаная В1NMВ3 – нижняя граница выигрыша, получаемого игроком А. Точка N, в которой выигрыш максимален, определяет цену игры и ее решение. Для нахождения оптимальной стратегии игрока А достаточно составить уравнения прямых и найти точку пересечения прямых В2В2 и В3В3. Уравнение прямой, проходящей через 2 точки (x1,y1) и (x2,y2) имеет вид
Вычтем из первого уравнения второе, получаем -11x=-8 Þx=8/11, y=3+2x=49/11. Точка N(8/11,49/11), следовательно, p2=8/11, p1=1-8/11=3/11, n=49/11. Таким образом, Из рисунка видно, что стратегия В1 не входит в оптимальную смешанную стратегию,поэтому q3=0,и мы можем найти оптимальную смешанную стратегию, удалив из платежной матрицыпервый столбец. Получаем матрицу Так как для стратегии А1: для стратегии А2: С учетом того, что сумма вероятностей смешанной стратегии равна 1, цена игры
Вычтем из первого уравнения второе:
Решая систему, находим
Оптимальная смешанная стратегия для игрока В Ответ: Пример 6 Решить графически игру, заданную платежной матрицей Решение Матрица игры имеет размер 4х2, поэтому решение игры будем искать для игрока В. Аналогично примеру 5отложим отрезок единичной длины В1В2, каждой точке которого поставим в соответствие некоторую смешанную стратегию второго игрока – (q1, q2). В частности, точке В1соответствует стратегия В1, точке В2 – стратегия В2. В точках В1 и В2 восстановим перпендикуляр и на полученных прямых будем откладывать выигрыши игрока А при соответствующих стратегиях и строить прямые, соответствующие стратегиям игрока А.
В соответствии с принципом минимакса ломаная А1NА4 – верхняя граница выигрыша, получаемого игроком А. Точка N, в которой выигрышминимален, определяет цену игры и ее решение. Для нахождения оптимальной стратегии игрока В достаточно составить уравнения прямых и найти точку пересечения прямых А1А1 и А4А4. Уравнение прямой, проходящей через 2 точки (x1,y1) и (x2,y2) имеет вид
Вычтем из первого уравнения второе, получаем 8x=5Þx=5/8, y=6-x=43/8. Точка N(5/8,43/8), следовательно, q2=5/8, q1=1-5/8=3/8, n=43/8. Таким образом, Из рисунка видно, что стратегииА2 и А3не входят в оптимальную смешанную стратегию,поэтому p2=0 и p3=0, имы можем найти оптимальную смешанную стратегию, удалив из платежной матрицывторую и третью строку. Получаем матрицу Так как для стратегии В1: для стратегии В2: С учетом того, что сумма вероятностей смешанной стратегии равна 1, цена игры
Вычтем из первого уравнения второе:
Решая систему, находим
Оптимальная смешанная стратегия для игрока А Ответ: Таким образом, имеем следующийалгоритм графического решения простейших матричных игр 2хn ( или mx2): 1. Строимn (m) прямых, соответствующих стратегиям второго (первого) игрока. 2. Строим нижнюю (верхнюю) границу выигрыша. 3. Выбираем на границе выигрыша точку с максимальной (минимальной) ординатой. 4. Определяем по чертежу пару активных стратегий из числа построенных для второго (первого) игрока. 5. Находим координаты точки максимума (минимума) и решение игры. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 672. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
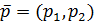 и
и  –смешанные стратегии игроков. Найдем оптимальные смешанные стратегии игроков. Если игрок В придерживается стратегии В1, то средний выигрыш А составит
–смешанные стратегии игроков. Найдем оптимальные смешанные стратегии игроков. Если игрок В придерживается стратегии В1, то средний выигрыш А составит  . Если игрок В придерживается стратегии В2, то средний выигрыш А составит
. Если игрок В придерживается стратегии В2, то средний выигрыш А составит  . По свойству оптимальных смешанных стратегий эти средние выигрыши должны совпадать и быть равными цене игры. Получаем систему:
. По свойству оптимальных смешанных стратегий эти средние выигрыши должны совпадать и быть равными цене игры. Получаем систему:

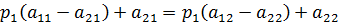
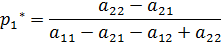






 .
.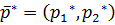 и соответствующую цену игрыn.
и соответствующую цену игрыn. – оптимальная, то она должна гарантировать средний выигрыш игроку А, равный цене игры, при любом поведении игрока В:
– оптимальная, то она должна гарантировать средний выигрыш игроку А, равный цене игры, при любом поведении игрока В: ;
; .
.
 или
или  .Значит:
.Значит:
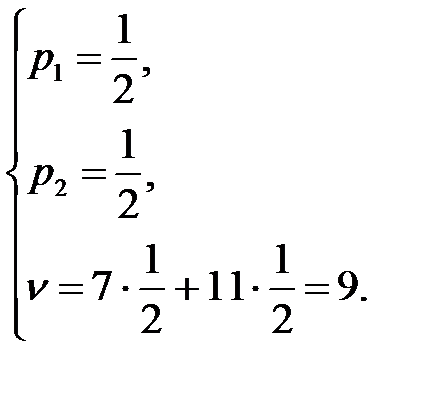
 , n = 9.
, n = 9.
 Откуда,
Откуда,  подставим в первое уравнение (Вместо n подставим найденное значение для игрока А
подставим в первое уравнение (Вместо n подставим найденное значение для игрока А



 .
. .
. =(0,67; 0,33) можно сделать вывод, что результаты моделирования достаточно близко соответствуют теоретическим вероятностям даже для небольшого количества партий.
=(0,67; 0,33) можно сделать вывод, что результаты моделирования достаточно близко соответствуют теоретическим вероятностям даже для небольшого количества партий.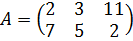 .
.
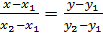 .Прямая В2В2 проходит через точки (0,3) и (1,5), следовательно, ее уравнение
.Прямая В2В2 проходит через точки (0,3) и (1,5), следовательно, ее уравнение  или -2x+y=3.Прямая В3В3 проходит через точки (0,11) и (1,2), следовательно, ее уравнение
или -2x+y=3.Прямая В3В3 проходит через точки (0,11) и (1,2), следовательно, ее уравнение  или 9x+y=11. Для нахождения точки пересечения прямых В2В2 и В3В3 решим систему:
или 9x+y=11. Для нахождения точки пересечения прямых В2В2 и В3В3 решим систему:
 , при цене игры
, при цене игры  .
. , при этом столбцы ее соответствуют активным стратегиям В2, В3.
, при этом столбцы ее соответствуют активным стратегиям В2, В3.
 .
.


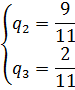
 .
.
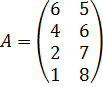 .
.
 или x+y=6.Прямая А4А4 проходит через точки (0,1) и (1,8), следовательно, ее уравнение
или x+y=6.Прямая А4А4 проходит через точки (0,1) и (1,8), следовательно, ее уравнение 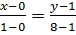 или -7x+y=1. Для нахождения точки пересечения прямых А1А1 и А4А4решим систему:
или -7x+y=1. Для нахождения точки пересечения прямых А1А1 и А4А4решим систему: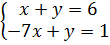
 , при цене игры
, при цене игры  .
.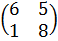 , при этом строки ее соответствуют активным стратегиям А1, А4.
, при этом строки ее соответствуют активным стратегиям А1, А4.
 .
.



 .
.