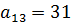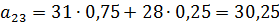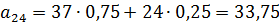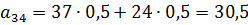Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Сведение матричной игры к задаче линейного программированияЕсли у каждого из игроков больше двух возможных стратегий, то можно решение игры свести к решению задачи линейного программирования. Найдем решение игры с платежной матрицейm´n:
Пусть матрица игры не содержит седловой точки. Тогда решение игры будем искать в смешанных стратегиях `p= (p1, p2, …, pm) и `q = (q1, q2, …, qm), где p1 + p2 +… + pm = 1 и q1 + q2 +… + qn = 1 Стратегия
Будем считать, что цена игры n больше нуля. Действительно, если n£ 0, то это означает, что некоторые элементы матрицы игры не положительные. Тогда найдём число M>0, которое прибавим ко всем элементам матрицы игры и получим новую матрицу с положительными элементами. Это сложение сделает цену новойигры, равную n+M, положительной, но не изменит решения игры. Разделим обе части всех неравенств на положительное число n и обозначим
тогда система ограничений примет вид
Далее, так как p1 + p2 +… + pm = 1, то Игрок A стремится максимизировать свой средний выигрыш n, то есть минимизировать отношение Таким образом, получаем задачу линейного программирования:
Заметим, что эта задача всегда имеет оптимальное решение Аналогичные рассуждения дают оптимальную стратегию
Обозначим Тогда для нахождения оптимальной смешанной стратегии игрока Bнеобходимо решить следующую задачу линейного программирования: 
Это двойственная задача к ранее составленной. Задача всегда имеет оптимальное решение Пример 7 Найти решение игры, заданной платежной матрицей: Решение: Найдем верхнюю и нижнюю цены игры.
a¹b, следовательно, игра не имеет седловой точки, решение будет в смешанных стратегиях. Чтобы свести матричную игру для игрока А к задаче линейного программирования преобразуем платежную матрицу так, чтобы все ее элементы были больше нуля – прибавим ко всем элементам матрицы число 4. Получаем преобразованную платежную матрицу:
Средний выигрыш А должен быть не меньше цены игры
Из условия p1 + p2 + p3 = 1,разделив обе части уравнения на n>0 (цена игры больше нуля, т.к. все элементы преобразованной матрицы больше нуля), получаем целевую функцию Перейдем в системе ограничений к переменнымxi, разделив каждое неравенство наn>0:
Таким образом, для нахождения оптимальной стратегии игрока А необходимо решить задачу линейного программирования:
Решим задачу средствами табличного редактора MSExcel.использованием настройкиПоиск решения. 1.Для решения нашей задачи создадим в Excel книгу с именем «Решение игры». Подготовим данные на листе. Сначала определим ячейки, в которые будет помещен результат решения. Пусть это будут ячейки В2, С2,D2, сделаем у них заголовки. В этих ячейках нет данных, их должен будет рассчитать Excel, они выделены цветом. Далее заполним коэффициенты при неизвестных и правые части системы ограничений (строки 5-7). Заведем строку 10 для целевой функции. Цветом выделена ячейка, в которой будет находиться значение целевой функции для найденного оптимального решения.
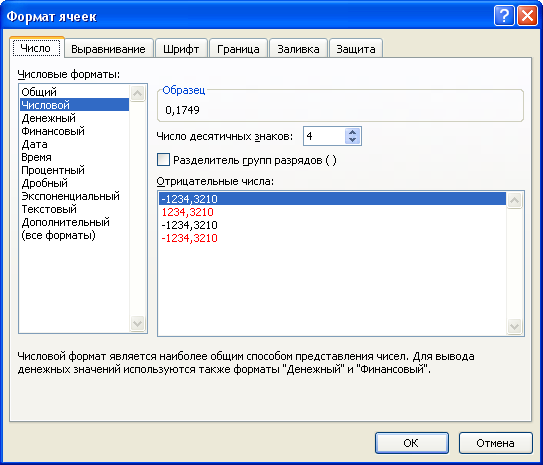
Для ячеек B2:D2 и D10 установим числовой формат с 4 знаками после запятой. Для этого выделим эти ячейки, в контекстном меню по правой кнопке мыши выберем команду Формат ячеек… и в появившемся окне Формат ячеек на вкладке Число установим нужный формат.
В ячейки F5, F6, F7 ведем формулы для зависимостей левых частей системы ограничений, а в ячейку D10 – формулу для зависимости целевой функции.
2.Далее необходимо воспользоваться надстройкой Поиск решения. На вкладке Данные в группе Анализ выберитекомандуПоиск решения. Появится диалоговое окно Поиск решения, которое необходимо заполнить следующим образом (для добавления ограничений пользуемся кнопкой Добавить):
Далее нажимаем кнопку Параметры и в появившемся окне Параметры поиска решенийустанавливаем флажок неотрицательные значения, линейная модель и нажимаем OK.
В окне Поиск решения после нажатия кнопкиВыполнить появляется окно Результаты поиска решения, в котором выбираем сохранение найденных значений и нажимаем кнопку ОК.
Результаты поиска решений:
Получили Окончательный результат: Аналогично можно составить и решить задачу линейного программирования для игрока В. Средний проигрыш игрока В должен быть не больше цены игры
Из условия q1 + q2 + q3 = 1,разделив обе части уравнения на n>0, получаем целевую функцию Перейдем в системе ограничений к переменнымyj, разделив каждое неравенство наn>0:
Таким образом, для нахождения оптимальной стратегии игрока А необходимо решить задачу линейного программирования:
Решим задачу средствами табличного редактора MSExcel.использованием настройкиПоиск решения. 1.Подготовим данные на листе.
В ячейки F5, F6, F7 ведем формулы для зависимостей левых частей системы ограничений, а в ячейку D10 – формулу для зависимости целевой функции. 2. Далее необходимо воспользоваться надстройкой Поиск решения.
В окне Параметры поиска решений устанавливаем флажок неотрицательные значения. Результаты поиска решений:
Получили Окончательный результат: Ответ: Игры с природой В рассмотренных ранее задачах теории игр предполагалось, в них принимают участие 2 участника, интересы которых противоположны. Поэтому действия каждого игрока направлены на увеличение выигрыша или уменьшение проигрыша. Однако во многих задачах теории игр отсутствует информация об условиях, в которых осуществляется действие. Эти условия зависят не от сознательного действия другого игрока, а от объективной действительности, которую принято называть природой. Такие игры называются играми с природой. Под термином «природа» понимается весь комплекс внешних условий, в которых человеку приходится принимать решение. Природа безразлична к выигрышу и не стремится обратить в свою пользу промахи человека. В играх с природой игрок А - человек или группа лиц, объединенных общностью цели, который называется статистиком. Возможные стратегии природы определяются как ее состояния (например, условия погоды, спрос на продукцию). Человеку могут быть известны вероятности, с которыми природа реализует свои состояния. Пусть статистик может использовать m стратегий А1, А2, …, Аm, а природа может реализовывать nразличных состояний Р1, Р2, …, Рn.Условия игры с природой так же задаются платежной матрицей
При выборе оптимальной стратегии статистика используют ряд критериев. При этом опираются как на платежную матрицу, так и на матрицу рисковR. Элементы матрицы rijпредставляют разность между максимальным выигрышем, который получил бы статистик, если бы достоверно знал, что природа будет находиться в состоянии Pj, и выигрышемаij, который он получит, используя стратегию Аi, т.е.
Рассмотрим критерии: 1. Критерий недостаточного основания Лапласа. Все состояния природы считаются равновероятными. В качестве оптимальной принимается чистая стратегия, при которой максимизируется средний выигрыш, т.е. для которой достигается максимум величины 2. Максиминный критерий Вальда. В качестве оптимальной выбирается стратегия, при которой наименьший выигрыш статистика будет максимальным, т.е. равен нижней цене игры для двух лиц с нулевой суммой. Для этого находится 3. Критерий минимаксного риска Сэвиджа В качестве оптимальной выбирается стратегия, при которой минимизируется максимальная величина риска.Для этого находится Критерии Вальда и Сэвиджа основаны на пессимистической оценке обстановки. Следующий критерий учитывает как пессимистический, так и оптимистический подход к ситуации. 4. Критерий Гурвица. Принимается решение о выборе стратегии, при которой достигается Обычно анализ практических ситуаций проводится по нескольким критериям одновременно, что позволяет выбрать наиболее обоснованное решение. Пример 8 Сельскохозяйственное предприятие планирует посадить некоторую сельскохозяйственную культуру двух сортов. Посевная площадь1 га. Сорта отличаются друг от друга требованиями к влаге во время вегетационного периода. Проанализировав погодные условия, выделены 4 состояния погоды (S1,S2,S3,S4), отличающиеся режимом осадков. Средняя урожайность (ц/га) каждого сорта на всем участке для каждого состояния погоды приведена в таблице:
Возможные варианты посева: А1) сорт 1 посадить на 100% площади; А2) сорт 1 посадить на 75% площади, сорт 2 посадить на 25% площади; А3) сорт 1 посадить на 50% площади, сорт 2 посадить на 50% площади; А4) сорт 1 посадить на 25% площади, сорт 2 посадить на 75% площади; А5) сорт 2 посадить на 100% площади; Определить оптимальную стратегию с помощью критериев недостаточного основания Лапласа, максиминного критерия Вальда, критерия минимаксного риска Сэвиджа, пессимизма-оптимизма Гурвица (коэффициент пессимизма взять равным 0,4). Решение Составим платежную матрицу игры. Рассчитаем ее элементы:
Платежная матрица:A Результаты расчетов будем заносить в таблицу:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 459. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 является оптимальной, то есть при любой стратегии игрока B средний выигрыш игрока A будет больше или равен цены игры n, таким образом, получаем систему ограничений
является оптимальной, то есть при любой стратегии игрока B средний выигрыш игрока A будет больше или равен цены игры n, таким образом, получаем систему ограничений
 .
.
 .
.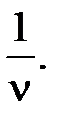
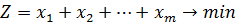
 . Его можно найти симплекс-методом или с использованием средств Excel.Тогда цена игры
. Его можно найти симплекс-методом или с использованием средств Excel.Тогда цена игры 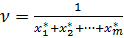 . Оптимальная смешанная стратегия первого игрока
. Оптимальная смешанная стратегия первого игрока  , где
, где 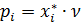 .
. игрока B. При любой стратегии игрока А проигрыш игрока В не должен превышать цену игры. Получаем систему ограничений:
игрока B. При любой стратегии игрока А проигрыш игрока В не должен превышать цену игры. Получаем систему ограничений:
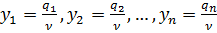 .
.

 ,которое можно найти симплекс-методом или по теореме равновесия, зная решение ранее составленной задачи. Тогда цена новой игры
,которое можно найти симплекс-методом или по теореме равновесия, зная решение ранее составленной задачи. Тогда цена новой игры  . Оптимальная смешанная стратегия второго игрока
. Оптимальная смешанная стратегия второго игрока 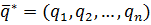 , где
, где 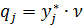 .
.

 при любом поведении игрока В. Так, если игрок В использует свою первую стратегию, то средний выигрыш игрока А составит:
при любом поведении игрока В. Так, если игрок В использует свою первую стратегию, то средний выигрыш игрока А составит: 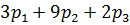 ,
,  . Аналогично, записав неравенства для стратегий В2 и В3, получаем систему линейных ограничений:
. Аналогично, записав неравенства для стратегий В2 и В3, получаем систему линейных ограничений:
 . Цель игрока А – получить максимальный средний выигрыш, т.е. n®max, а значит
. Цель игрока А – получить максимальный средний выигрыш, т.е. n®max, а значит  . Если обозначить
. Если обозначить 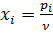 (i=1, 2, 3), то целевая функция
(i=1, 2, 3), то целевая функция  .
.







 . Так как
. Так как  и
и  , то находим, что
, то находим, что  – это решение для игры, заданной преобразованной матрицей. Для исходной матрицы компоненты смешанной стратегии не меняются, а цена игры меньше на число, которое прибавляли ко всем элементам матрицы, т.е. на 4.
– это решение для игры, заданной преобразованной матрицей. Для исходной матрицы компоненты смешанной стратегии не меняются, а цена игры меньше на число, которое прибавляли ко всем элементам матрицы, т.е. на 4. .
.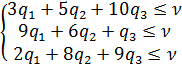
 . Цель игрока В – получить минимальный средний проигрыщ, т.е. n®min, а значит
. Цель игрока В – получить минимальный средний проигрыщ, т.е. n®min, а значит  . Если обозначить
. Если обозначить 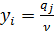 , (j=1, 2, 3), то целевая функция
, (j=1, 2, 3), то целевая функция  .
.


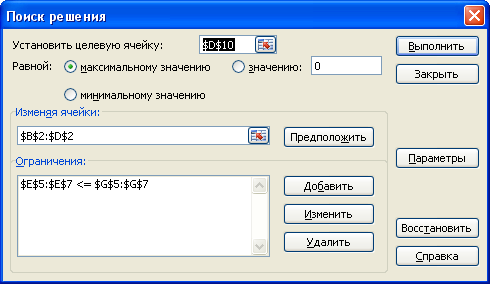

 . Так как
. Так как  и
и  , то находим, что
, то находим, что 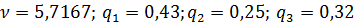 – это решение для игры, заданной преобразованной матрицей.
– это решение для игры, заданной преобразованной матрицей. .
. ,
,  , в которой элемент аij равен выигрышу статистика, если он использует стратегию Аi, а природа находится в состоянии Pj.
, в которой элемент аij равен выигрышу статистика, если он использует стратегию Аi, а природа находится в состоянии Pj. , где
, где  .
. .
.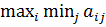 .
.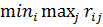 .
. , где 0£l£1. Значение l выбирают на основе субъективных соображений. Чем больше желание подстраховаться, тем ближе к 1 значение l.
, где 0£l£1. Значение l выбирают на основе субъективных соображений. Чем больше желание подстраховаться, тем ближе к 1 значение l.