Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
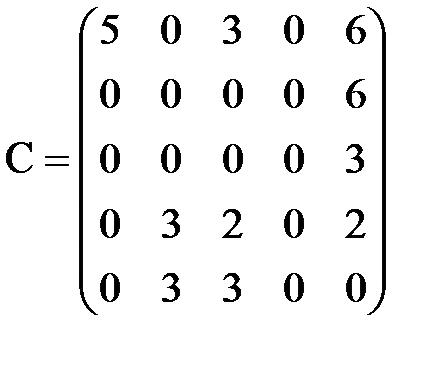
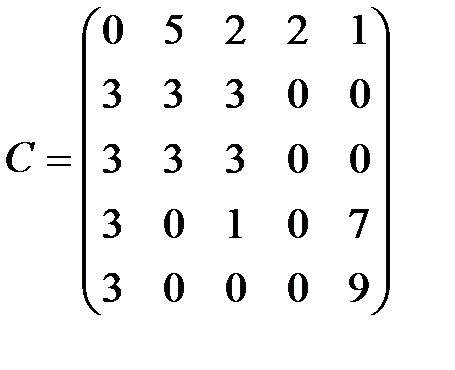
Специальные задачи линейного программированияЗадача о назначениях Пример 1 В каждом из пяти филиалов производственного объединения могут изготовляться изделия пяти видов. Учитывая необходимость углубления специализации, в каждом из филиалов решено выпускать только один вид продукции, при этом каждый из видов изделий должен выпускаться одним из филиалов. Себестоимость каждого изделия в каждом из филиалов различна и задается матрицей C (
Составим математическую модель задачи.
i = 1,2,3,4,5, j= 1,2,3,4,5 Каждое филиал должен выпускать только один вид продукции:
Каждая вид продукции должен выпускаться:
Условие неотрицательности переменных: xij³ 0, i = 1,2,3,4,5, j = 1,2,3,4,5 Суммарная себестоимость выпущенной продукции: Z = 5x11 + 11x12 + 6x13 + 11x14 + 4x15 + 10x21 + 11x22 + 9x23 + 11x24+ 5x25 + 7x31 + + 8x32 + 6x33 + 8x34 + 2x35 + 6x41 + 4x42 + 3x43 + 7x44+ 8x45+ 4x51 + 2x52 + 5x54 + Подобную задачу можно решать симплекс-методом, но можно использовать специальный метод – венгерский метод. Алгоритм венгерского метода: 1 этап 1. В каждой строке находим минимальный элемент и вычитаем его из всех элементов соответствующей строки. 2. В каждом столбце находим минимальный элемент и вычитаем его из всех элементов соответствующего столбца. 2 этап 1. Проводим минимальное количество вертикальных и горизонтальных линий, пересекающих все нули. 2. Если таких количество таких линий равно количеству строк матрицы С, то 2-ой этап завершен. 3. В противном случае выберем среди неперечеркнутых элементов минимальный и построим новую матрицу по правилам:  а) из неперечеркнутых элементов вычитаем минимальный элемент; б) к элементам, через которые проведены две линии, прибавляем минимальный элемент; в) все остальные элементы не меняем. Далее переходим на п.3 3 этап В построении решения участвует последняя матрица из этапа 2. 1.Находим строку или столбец матрицы, в которой имеется единственный 0. Если такой строки или столбца нет, то берем любую строку или столбец, содержащие нули.Пусть 2. Тогда в матрице X 3. В матрице С вычеркиваем i-ю строку и j-ый столбец. 4. Если в матрице С остался один элемент, то соответствующий элемент матрицы Xравен 1 и этап 3 закончен. Иначе переходим на п.1. Решим сформулированную выше задачу. Этап 1
 

Этап 2



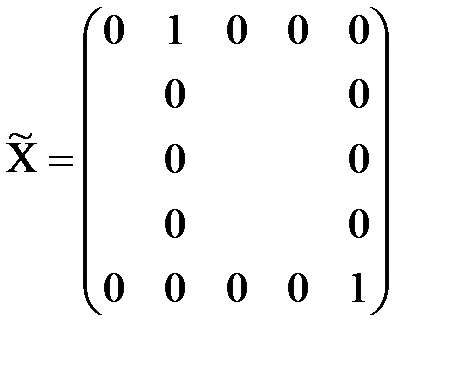
Этап 3 Порядок составления матрицы X: 1. Т.к. в 1-ой строке преобразованной матрицы имеется единственный элемент равный 0 (c11=0), то x11=1, а все остальные элементы 1-ой строки и 1-го столбца матрицы X равны 0. В матрице С исключаем из дальнейшего рассмотрения 1-ю строку и 1-ый столбец. 2. Среди оставшихся невычеркнутыми элементов матрицы С 3-ий столбец содержит единственный 0 (c53=0). Поэтому считаем, что x53=1, а все остальные элементы 5-ой строки и 3-го столбца матрицы X равны 0. В матрице С исключаем из дальнейшего рассмотрения 5-ю строку и 3-ий столбец. 3. Среди оставшихся невычеркнутыми элементов матрицы С второй столбец содержит единственный 0 (c42=0). Поэтому считаем, что x42=1, а все остальные элементы 4-ой строки и 2-го столбца матрицы X равны 0. В матрице С исключаем из дальнейшего рассмотрения 4-ю строку и 2-ой столбец. 4. Среди оставшихся невычеркнутыми элементов матрицы С нет строк или столбцов, содержащих единственный 0. Поэтому выбираем любой нулевой элемент (например, c24=0) и считаем, что x24=1, а все остальные элементы 2-ой строки и 4-го столбца матрицы X равны 0. В матрице С исключаем из дальнейшего рассмотрения 2-ю строку и 4-ый столбец.
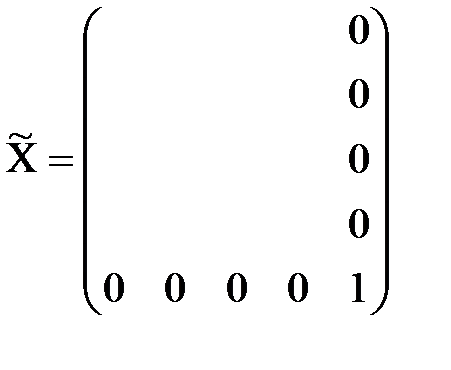
5. Т.к. c35=0, то x35=1. Итак, оптимальное решение задачи о назначениях:
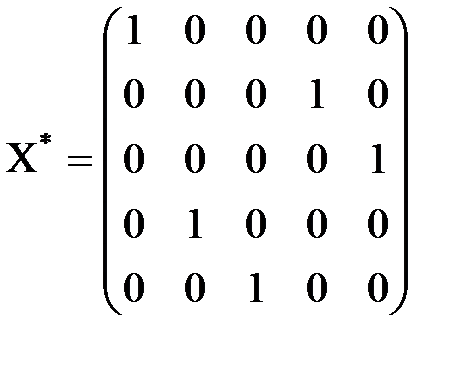
Zmin= 5 + 11 + 2 + 4 + 0 = 22. Решим задачу о назначениях с использованием средств MSExcel. Для решения нашей задачи создадим в Excelкнигу с именем «Решение задачи о назначениях». Подготовим данные на листе. Сначала определим ячейки, в которые будут вводиться элементы матрицы С. Пусть это будут ячейки B3:F7. Заполним их и оформим заголовки строк и столбцов. Определим ячейки, куда будет помещен результат решения. Пусть это будут ячейки B12:F17, сделаем у них заголовки. В этих ячейках нет данных, их должен будет рассчитать Excel, они выделены цветом. Заведем строку 18 для целевой функции. Цветом выделена ячейка, в которой будет находиться значение целевой функции для найденного оптимального решения.
В ячейки G12:G16 введем нахождение сумм неизвестных по строкам, в ячейки B17:F17 –нахождение сумм неизвестных по столбцам, в ячейку D18 – формулу для нахождения целевой функции.
Далее необходимо воспользоваться надстройкой Поиск решения. На вкладке Данные в группе Анализ выберитекомандуПоиск решения. Появится диалоговое окно Поиск решения, которое необходимо заполнить следующим образом (для добавления ограничений пользуемся кнопкой Добавить):
Далее нажимаем кнопку Параметры и в появившемся окне Параметры поиска решений устанавливаем флажок неотрицательные значения, линейная модель и нажимаем OK.
В окне Поиск решения после нажатия кнопкиВыполнить появляется окно Результаты поиска решения, в котором выбираем сохранение найденных значений и нажимаем кнопку ОК.
Результаты поиска решений:
Получили Интерпретация решения: Первый филиал должен выпускать 1-ый вид изделий, второй филиал должен выпускать 4-ый вид изделий, третий филиал должен выпускать 5-ый вид изделий, четвертый филиал должен выпускать 2-ой вид изделий, пятый филиал должен выпускать 3-ий вид изделий. При таком распределении себестоимость выпуска изделий будет минимальна и составит 22 у.е. Алгоритм решения задачи о назначениях предполагает минимизацию ее целевой функции. Если имеется задача о назначениях, целевую функцию которой нужно максимизировать, то поступают таким же образом, как и при переходе от одной формы записи к другой в задаче линейного программирования: все элементы матрицы умножаются на (- 1) и далее решают как в случае минимизации. Если матрица С не является квадратной, в нее следует включить дополнительные фиктивные строки и столбцы, необходимые для приведения ее к квадратной форме. Значения стоимости, соответствующие фиктивным клеткам, как правило, равны нулю.Назначения, размещаемые в клетках фиктивных строк, фактически не существуют. Назначения, соответствующие фиктивным столбцам, на деле представляют собой те единицы, которые не подлежат распределению. Пример 2 В цехе предприятия имеются 5 универсальных станков, которые могут выполнять четыре вида работ. Производительность каждого станка при выполнении каждой работы задается матрицей С. Найти наиболее рациональное распределение работ между станками, максимизирующее суммарную производительность станков, если каждый станок можно загружать только одной работой.
Составим математическую модель задачи: Пусть
i = 1,2,3,4,5, j = 1,2,3,4 Каждый станок должен выполнять не более одной работы
Каждая работа должна выполняться только одним станком:
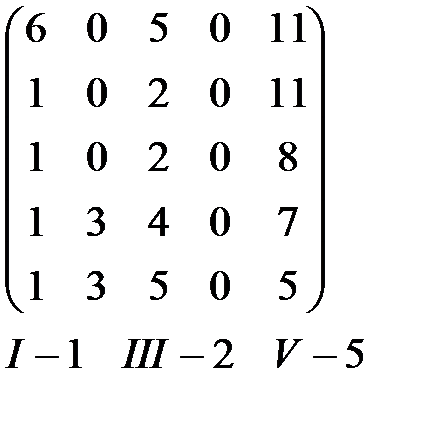
Условие неотрицательности переменных: xij³ 0, i = 1,2,3,4,5, j = 1,2,3,4 Суммарная производительность: Z = 5x11 + 11x12 + 6x13 + 11x14 + 10x21 + 11x22 + 9x23 + 11x24+ 7x31 + 8x32 +6x33 + Т.к. матрица С не квадратная, то введем фиктивный 5-ый вид работ с нулевыми производительностями для всех станков.
Этап 1
Этап 2

Этап 3 Порядок составления матрицы X: 1. Т.к. в 5-ом столбце преобразованной матрицы имеется единственный элемент равный 0 (c55=0), то x55=1, а все остальные элементы 5-го столбца и 5-ой строки матрицы X равны 0. В матрице С исключаем из дальнейшего рассмотрения 5-ю строку и 5-ый столбец. 2. Среди оставшихся невычеркнутыми элементов матрицы С нет строки или столбца, содержащих единственный 0. Поэтому, выберем любой 0 , например, c12=0. Поэтому считаем, что x12=1, а все остальные элементы 1-ой строки и 2-го столбца матрицы X равны 0. В матрице С исключаем из дальнейшего рассмотрения 1-ю строку и 2-ой столбец. 3. Среди оставшихся невычеркнутыми элементов матрицы С нет строки или столбца, содержащих единственный 0. Поэтому, выберем любой 0, например, c21=0. Поэтому считаем, что x21=1, а все остальные элементы 2-ой строки и 1-го столбца матрицы X равны 0. В матрице С исключаем из дальнейшего рассмотрения 2-ю строку и 1-ый столбец. 4. Т.к. в 3-ем столбце преобразованной матрицы имеется единственный элемент равный 0 (c33=0), то x33=1, а все остальные элементы 3-го столбца и 3-ей строки матрицы X равны 0. В матрице С исключаем из дальнейшего рассмотрения 3-ю строку и 3-ий столбец. 5. Т.к. c44=0, то x44=1. Итак, оптимальное решение задачи о назначениях:
Zmax= 11 + 10 + 6 + 7 = 34. Интерпретация решения: Первыйстанок должен выполнять 2-ю работу, второй – 1-ю работу, третийстанок – 3-ю работу, четвертыйстанок – 4-ю работу, пятыйстанок не будет выполнять никакой работы. При таком распределении работ производительность будет максимальна и составит 34 единицы. Теория игр Основные понятия При решении ряда практических задач в области экономики, политики и военного дела приходится принимать решения в ситуациях, в которых сталкиваются интересы двух или более сторон, которые преследуют противоположные цели, причём результат любого действия каждой из сторон зависит от того, какое действие предпримет противник. Такие ситуации называются конфликтными. Примеры конфликтных ситуаций: - любая ситуация в ходе военных действий; - планирование военных операций; - конкурентная борьба в экономике; - выборы в парламент; - салонные игры (например, шашки, шахматы, карты) . Теория игр – математическая теория конфликтных ситуаций, ее цель - выработать рекомендации по рациональному образу действий участников конфликтной ситуации. При этом не учитываются элементы риска, просчеты и ошибки игроков. · Для математического анализа конфликтной ситуации отбрасывают второстепенные факты и строят формализованную модель конфликтной ситуации – игру. Конфликтные стороны называются игроками. Игра ведется по определенным правилам. Правила игры устанавливают возможные действия игроков, объём сведений каждой стороны о поведении другой,результат, к которому приводит каждая совокупность ходов. Правила определяют так же конец игры, когда больше ходов делать не разрешается. Каждый игрок делает ход – выбор одного из вариантов действий, предусмотренных правилами игры. Ходы бывают личные и случайные. Личный ход – сознательный выбор игроком допустимого действия. Случайный ход – выбор допустимого действия с помощью механизма случайного выбора (например, подбрасывания монеты) и его осуществление. Будем считать, что в конце игры любой игрок получает выигрыш. Можно провести классификацию игр: - По числу игроков: · одного лица (например, пасьянс); · двух лиц – парная игра (например, шахматы); · n лиц – множественная (они делятся на коалиационные, когда несколько лиц могут заключить союз, и бескоалиационные). - По количеству и характеру ходов: · с полной информацией (например, шахматы); · с неполной информацией (например,карты. Большинство игр - с неполной информацией). - По количеству ходов: · конечные (у каждого игрока имеется конечное количество ходов); · бесконечные (например, дуэль). - По выигрышу: · с нулевой суммой (парная игра, в которой выигрыш одной стороны равен проигрышу другой); · с ненулевой суммой (например, экономические процессы создают или уничтожают богатство). Стратегией игрока называется совокупность правил, определяющая выбор варианта действий при каждом ходе игрока в зависимости от ситуации, сложившийся в игре.Игра m´n– конечная парная игра, в которой у одного игрока имеется m стратегий, а у второго n стратегий. Далее будем рассматривать парные игры m´nс нулевой суммой. Пусть имеется игра двух игроков Aи B. Пусть у игрока Aимеется mстратегий A1, A1,…, Am, а у игрока Bимеется nстратегий B1, B1,…, Bn.
Пример 1. (Игра "поиск"). Игрок A прячется в одном из двух убежищ, а игрок B его ищет. Правила игры: если игрок B находит A, то A платит ему 1 рубль, в противном случае игрок B платит A 1 рубль. Стратегии игроков: игрок A: A1 – спрятаться в убежище № 1, A2 – спрятаться в убежище № 2; игрок B: B1 – искать в убежище № 1, B2 – искать в убежище № 2; Платежная матрица:
Это игра с неполной информацией. Если игра проводится один раз, то бессмысленно говорить о разумных стратегиях. Любой игрок с одинаковым основанием может применять любую стратегию. Но если игра многократно повторяется, то положение меняется. Если игрок будет придерживаться одной стратегии или чередования стратегий в определённой последовательности, то противник догадается об этом и начнёт выигрывать. Поэтому от верного проигрыша игроков может спасти только случайное чередование стратегий. Например, игрок перед своим ходом подбрасывает монету и, если выпала "решка", то игрок выбирает первую стратегию, а если "орёл", то вторую. Оптимальной стратегией называется стратегия, которая при многократном повторении игры обеспечивает игроку максимально возможный средний выигрыш. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 389. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 - себестоимость производства i-м филиалом j-го вида продукции). Найти распределение выпуска продукции между филиалами, чтобы общая себестоимость выпущенной продукции была минимальной.
- себестоимость производства i-м филиалом j-го вида продукции). Найти распределение выпуска продукции между филиалами, чтобы общая себестоимость выпущенной продукции была минимальной.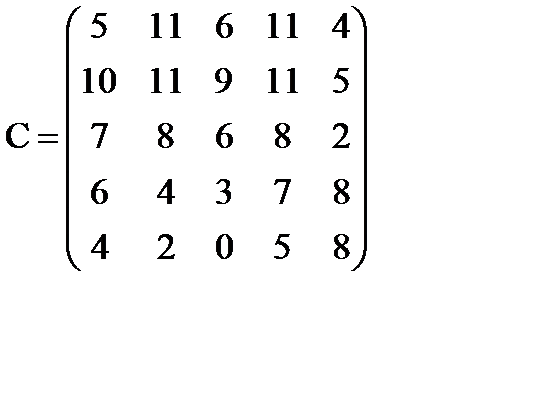



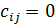 .
.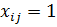 и все остальные элементы i-ой строки и j-го столбца равны 0.
и все остальные элементы i-ой строки и j-го столбца равны 0.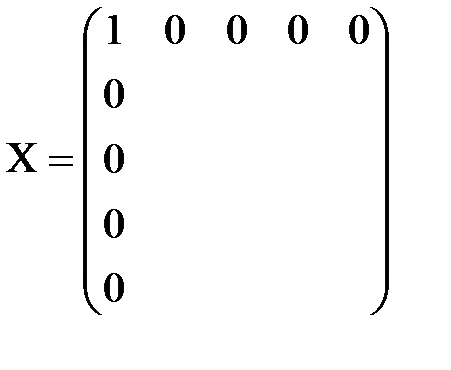










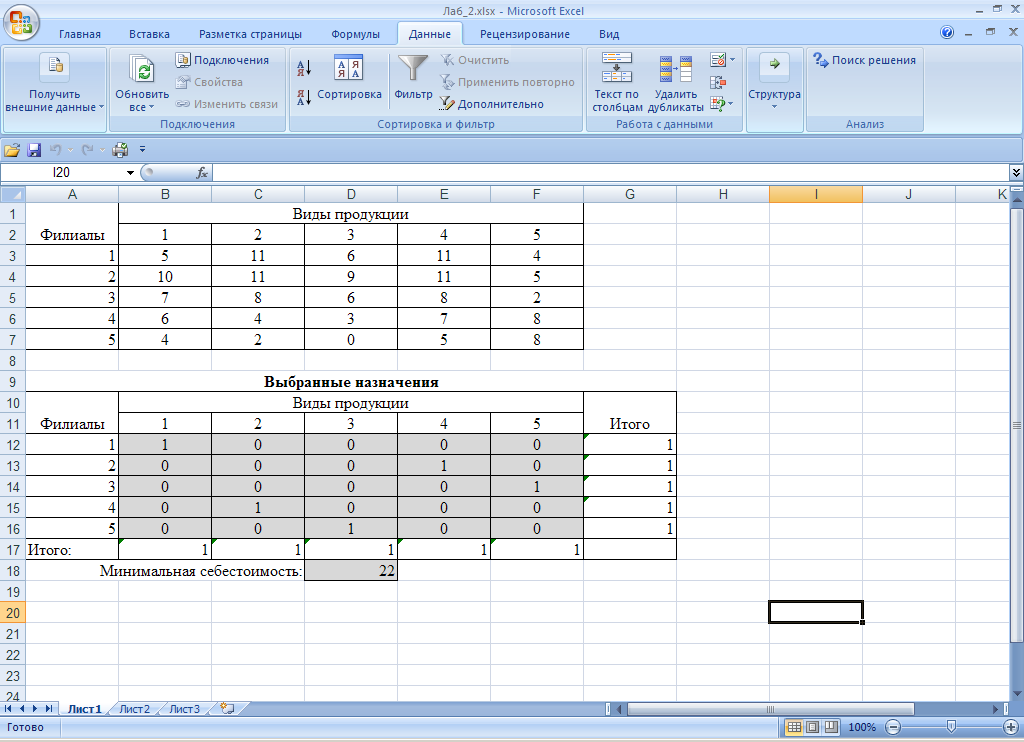
 .Решение совпадает с найденным венгерским методом.
.Решение совпадает с найденным венгерским методом.