
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Нижняя и верхняя цены игры. Принцип минимаксаДополним матрицу игры столбцом с минимальными значениями в строках и строкой с максимальными значениями в столбцах:
Величина Стратегия игрока A, соответствующая максимину a, называется максиминной стратегией игрока A.Если игрок A придерживается своей максиминной стратегии, то ему гарантирован выигрыш не меньше a, то есть a – это тот гарантированный минимальный выигрыш, который может обеспечить себе игрок A, придерживаясь наиболее осторожной стратегии. Величина Теорема 1Для игры двух лиц с нулевой суммой Если игрок B придерживается своей минимаксной стратегии, то ему гарантирован проигрыш не больше b. Положение, при котором игроки используют свои минимаксные стратегии неустойчиво и может быть нарушено поступившими сведениями о выбранной стратегии другого игрока. Если оба игрока разумны, то игрок A будет выбирать свою максиминную стратегию, а игрок B – минимаксную. Пример 2. Найдем нижнюю и верхнюю цены игры из примера 1.
Таким образом, если игрок Aбудет делать личные ходы, а его противник Bоб этом узнает, то игрок A получит минимальный выигрыш -1, то есть он будет в проигрыше, а игрок B получит минимальный проигрыш 1, то есть он будет выигрывать.Аналогичное утверждение справедливо и для игрока B.  Игра называется игрой с седловой точкой, если нижняя и верхняя цена игры совпадают.В этом случае, величина n = a = b называется чистой ценой игры.Седловой точке соответствует пара минимаксных стратегий, которые называются оптимальными, а их совокупность называется решением игры. В игре с седловой точкой любому игроку выгодно придерживаться оптимальных стратегий (любое отклонение от оптимальной стратегии ухудшает положение игрока). Чистая цена игры в игре с седловой точкой является значением выигрыша, которое в игре разумных противников игрок A не может увеличить, а игрок B уменьшить.При разумном поведении игроков исход игры с седловой точкой заранее предопределен. Играть в такие игры имеет смысл, если противник не знает оптимальной стратегии. Пример 3 Двое играют в следующую игру: одновременно выбрасывают 1, 2 или 3 пальца. Выигрывает тот, у кого больше пальцев (выигрыш равен разности выброшенных пальцев). Если оба выбросили одинаковое количество пальцев, то никто не выиграл. Платежная матрица:
Так как нижняя a и верхняя b цены игры совпадают, то игра имеет седловую точку, поэтому игра решается в чистых стратегиях с чистой ценой игры n = 0.Оптимальные стратегии сторон: оба игрока выбрасывают по 3 пальца. При этом никто не выигрывает. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 415. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

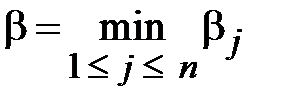
 называется нижней ценой игрыили максимином).
называется нижней ценой игрыили максимином).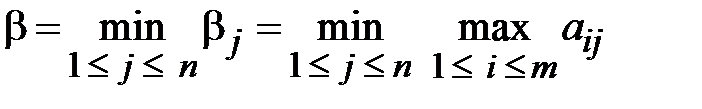 называется верхней ценой игрыили минимаксом.Стратегия игрока B, соответствующая минимаксу b, называется минимаксной стратегией игрока B.
называется верхней ценой игрыили минимаксом.Стратегия игрока B, соответствующая минимаксу b, называется минимаксной стратегией игрока B. .
.