
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Нелинейное программированиеВ общем случае задача нелинейного программирования (НП) состоит в нахождении экстремума (минимума или максимума) функции Z = f(x1,…, xn)® min (max), на множестве, задаваемом ограничениями в виде равенств и (или) неравенств, gi(x1,…, xn) =bi, gi(x1,…, xn) ≤ bi, Так же могут быть условия неотрицательности переменных. Предполагается, что среди функций f и gi ( Любой n-мерныйвектор x = (x1,…,xn), удовлетворяющий ограничениям задачи, называется допустимым решением, а множество X всех таких векторов — областью допустимых решений (ОДР). Перечислим свойства задач НП, которые существенно усложняют процесс их решения по сравнению с задачами линейного программирования: 1. Множество допустимых решений может иметь очень сложную структуру (например, быть невыпуклым или несвязным). 2. Глобальный максимум (минимум) может достигаться как внутри области, так и на ее границах (где он, вообще говоря, будет не совпадать ни с одним из локальных экстремумов). 3. Целевая функция f может быть недифференцируемой, что затрудняет применение классических методов математического анализа. Этим объясняется отсутствие общих методов, подобных симплекс-методу в линейном программировании, позволяющих решать любые задачи НП. Тем не менее, отдельные специальные классы нелинейных задач хорошо изучены. Графическое решение задачи нелинейного программирования  Графический метод можно использовать для решения задачи НП, которая содержит две переменных х1 и х2, например задачи следующего вида: Z = f(x1, x2)→ min (max); gi(x1, x2)≤ bi, Чтобы найти ее оптимальное решение, нужно выполнить следующие действия: 1. Найти ОДР, определяемую ограничениями задачи. Если окажется, что эта область пуста, то это означает, что задача не имеет решения. 2. Построить семейство линий уровня целевой функции f(х1, х2) = C при различных значениях числового параметра С. 3. При решении задачи на минимум определить направление убывания, а для задачи на максимум — направление возрастания линий уровня целевой функции. 4. Найти точку ОДР, через которую проходит линия уровня с наименьшим в задаче на минимум (соответственно, наибольшим в задачи на максимум) значением параметра С. Эта точка будет оптимальным решением. Если целевая функция не ограничена снизу в задаче на минимум (сверху — в задаче на максимум), то это означает, что задача не имеет оптимального решения. 5. Найти координаты точки оптимума и определить в ней значение целевой функции. Отметим, что в отличие от задачи линейного программирования точка оптимума в задаче НП не обязательно находится на границе ОДР. Ею также может быть внутренняя точка этого множества. Пример1 Найти максимальное и минимальное значение функции
При условиях Это задача НП, т.к. целевая функция нелинейна. Областью допустимых решений является треугольник АВС.
Строим линии уровня
Найдем координаты точке D, для этого воспользуемся равенством угловых коэффициентов прямой
Из условия
Решая систему, находим Следовательно, Координаты С найдем из системы:
Ответ: Метод множителей Лагранжа Рассмотрим частный случай задачи НП, предполагая, что система ограничений содержит только уравнения, отсутствуют условия неотрицательности и функции f(x1,…, xn) иgi(x1,…, xn) непрерывны вместе с частными производными. Z = f(x1,…, xn)® min (max); gi(x1,…, xn) =bi, Чтобы найти решение этой задачи вводят переменные L(x, λ) = L(x1,…, xn, λ 1,…, λm) = f(x1,…, xn) + находят частные производные функции Лагранжа по всем переменным xj и λiи приравнивают их нулю для нахождения стационарных точек функции Лагранжа. Получается система n + m уравнений:
Находятся решения этой системы. Среди этих решений после дополнительного анализа (проверки достаточного признака экстремума) отбираются такие, которые действительно являются точками локального оптимума. После сравнения значений целевой функции в этих точках находится точка, являющаяся глобальным оптимумом. Подчеркнем, что основное практическое значение метода Лагранжа заключается в том, что он позволяет перейти от условной оптимизации к безусловной и, соответственно, расширить арсенал доступных средств решения проблемы. Однако нетрудно заметить, что задача решения системы уравнений, к которой сводится данный метод, в общем случае не проще исходной проблемы поиска экстремума.Методы, подразумевающие такое решение, называются непрямыми. Они могут быть применены для весьма узкого класса задач, для которых удается получить линейную или сводящуюся к линейной систему уравнений. При решении конкретных практических задач обычно используются прямые методы, основанные на итерационных процессах вычисления и сравнения значений оптимизируемых функций. К таким методам относят градиентные методы решения задач безусловной оптимизации. |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 414. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
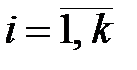 .
.  .
. 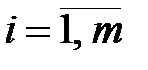 ) есть хоть одна нелинейная.
) есть хоть одна нелинейная. .
.
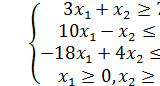
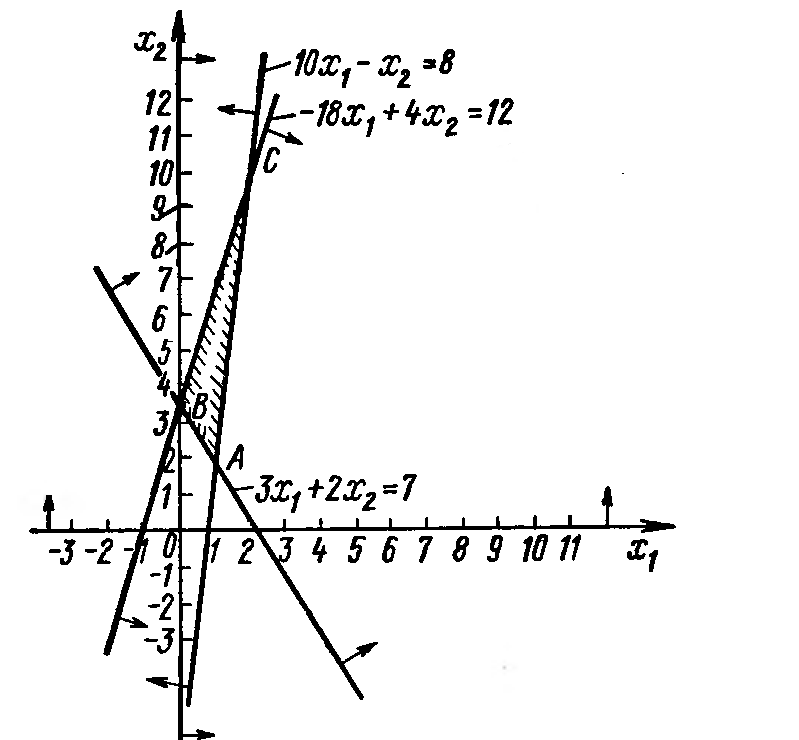
 – концентрические окружности с центром в точке Е(3;4). Видно, что минимум целевой функции достигается в точке D –точке касания окружности и области, максимальное значение функция принимает в точке С – угловой точке множества.
– концентрические окружности с центром в точке Е(3;4). Видно, что минимум целевой функции достигается в точке D –точке касания окружности и области, максимальное значение функция принимает в точке С – угловой точке множества. .
. и касательной к окружности. Для прямой выразим x2:
и касательной к окружности. Для прямой выразим x2:  , следовательно,k1=10. Для касательной к окружности угловой коэффициент – это производная x2 (находим производную неявной функции). Продифференцируем по x1 обе части уравнения окружности:
, следовательно,k1=10. Для касательной к окружности угловой коэффициент – это производная x2 (находим производную неявной функции). Продифференцируем по x1 обе части уравнения окружности:


 получаем уравнение
получаем уравнение  или
или 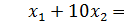 . Это одно из уравнений для нахождения координат точки D. Точка Dлежит на прямой
. Это одно из уравнений для нахождения координат точки D. Точка Dлежит на прямой 

 .
. . Решив которую, находим С(2;12).
. Решив которую, находим С(2;12).
 ,
, 
 .
. , называемые множителями Лагранжа и составляют функцию Лагранжа:
, называемые множителями Лагранжа и составляют функцию Лагранжа: λi(bi– gi(x1,…, xn)),
λi(bi– gi(x1,…, xn)), ;
; 