
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Решение игр в смешанных стратегияхЕсли игра не имеет седловой точки, то игрок A гарантирует себе выигрыш, равный нижней цене игры, которая меньше верхней цены игры.Конечно, игрок А хочет увеличить выигрыш, а В – уменьшить проигрыш. Если игроки будет чередовать свои стратегии случайным образом, то в некоторых случаях А получит бόльший выигрыш, чем нижняя цена игры. Смешанной стратегией игрока A называется набор вероятностей Теорема 2(Фон-Неймана) Для любойконечная игра m´nдвух лиц существуют смешанные стратегии
Экономический смысл теоремы: Если игрок А отступает от стратегии Теорема 3 (о цене игры) Цена игры удовлетворяет неравенству |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 320. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , где p1 + p2 +… + pm = 1, с которыми он чередует свои стратегииA1, A1,…, Am. Аналогично определяется смешанная стратегия игрока B как набор
, где p1 + p2 +… + pm = 1, с которыми он чередует свои стратегииA1, A1,…, Am. Аналогично определяется смешанная стратегия игрока B как набор  где q1 + q2 +… + qn = 1. В этом случае выигрыш А определяется как
где q1 + q2 +… + qn = 1. В этом случае выигрыш А определяется как 
 игрока А и
игрока А и  и игрока В, что для любых других стратегий
и игрока В, что для любых других стратегий 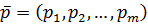 и
и  выполняется неравенство:
выполняется неравенство: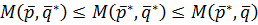
 , то его выигрыш уменьшается. Если игрок В отступает от стратегии
, то его выигрыш уменьшается. Если игрок В отступает от стратегии  , то его проигрыш увеличивается. Таким образом, смешанные стратегии
, то его проигрыш увеличивается. Таким образом, смешанные стратегии  образуют седловую точку во множестве смешанных стратегий, игрокам не выгодно отступать от стратегий, соответствующих этой точке. Если
образуют седловую точку во множестве смешанных стратегий, игрокам не выгодно отступать от стратегий, соответствующих этой точке. Если  - пара смешанных стратегий, образующих седловую точку, то величина
- пара смешанных стратегий, образующих седловую точку, то величина  называется ценой игры.
называется ценой игры.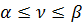 .
.