
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Графический способ метод решения ЗЛП, заданной в симметричной форме, в случае двух переменныхПусть задача линейного программирования с двумя переменными задана в симметричной форме.
Для решения этой задачи можно перебрать все вершины многоугольника, определяемого системой ограничений, и выбрать из них ту, в которой значение функции больше. Но можно не перебирать все вершины, а воспользоваться понятиями линии уровня и градиента. Линией уровня функции Z называется множество точек, удовлетворяющее уравнению Вектор Таким образом, наибольшее значение Z достигается в вершине, через которую проходит линия уровня, соответствующая наибольшему значению Z. Для графического решения задачи ЗЛП используют следующий алгоритм: 1. Записывают уравнения граничных прямых ai1x1+ai2x2=bi (i = 1,…,m) и строят их на плоскости X1OX2 по двум точкам. 2. Отмечают полуплоскости, соответствующие ограничениям - неравенствам. Для этого берут «пробную» точку, через которую не проходит граница полуплоскости (часто берут, если прямая не проходит через начало координат, точку (0,0)), и ее координаты подставляют в соответствующее ограничение - неравенство. Если полученное неравенство верное, то искомой будет полуплоскость, содержащая «пробную» точку; в противном случае, искомой будет полуплоскость, которой данная точка не принадлежит. 3. Заштриховывают многоугольник, определяемый системой ограничений. Для этого определяют общую часть ранее отмеченных m полуплоскостей, лежащую в первой четверти (следует из условий неотрицательности переменных).  4. Строят вектор 5. В случае необходимости параллельным переносом линию уровня следует расположить таким образом, чтобы многоугольник находился впереди линии уровня по направлению 6. Определяют экстремальную точку, соответствующую вершине многоугольника, путем параллельного перемещения прямой Z = с в направлении вектора 7. Вычисляют координаты оптимальной точки и значение функции Z в этой точке. Замечание: Если у функции требуется найти минимальное значение, то линию уровня Z = cперемещают в направлении вектора В зависимости от особенностей области допустимых решений и взаимного расположения области и вектора 1. Если область допустимых решений – ограниченный многоугольник, то может быть либо единственное решение, либо бесконечно много решений – все точки отрезка, соединяющего две вершины многоугольника (альтернативный оптимум). В случае альтернативного оптимума оптимальный план представляется выражением координат произвольной точки отрезка через координаты ее концов. 2. Если область допустимых решений – неограниченный многоугольник, то в зависимости от направления На рисунке а) функция достигает минимума в точке А, а максимума – в любой точке отрезка ВС (альтернативный оптимум); на рисунке б) максимум достигается в точке А, минимума функция не имеет; на рисунке в) функция не имеет ни минимума, ни максимума.
Пример 1 Решить графически ЗЛП:
Решение Каждое неравенство исходной системы ограничений определяет полуплоскость. Запишем уравнения граничных прямых для этих полуплоскостей.
Построим прямые.
2 × 0 + 5 × 0 £ 20 верно. Следовательно, отмечаем полуплоскость, содержащую «пробную» точку (0;0). 8 × 0 + 5 × 0 £ 40 верно. Следовательно, отмечаем полуплоскость, содержащую «пробную» точку (0;0). 5 × 0 + 6 × 0 £ 30 верно. Следовательно, отмечаем полуплоскость, содержащую «пробную» точку (0;0). Выбранные полуплоскости отметим стрелочками. Найдем пересечение отмеченных полуплоскостей с учетом условия: х1,х2³ 0. Заштрихуем полученный пятиугольник. Построим линию уровня Z = 0: 50х1 + 40х2 = 0
Вектор Перемещая линию уровня параллельным переносом в направлении вектора
8х1 + 5х2 = 40 ´ 5 5х1 + 6х2 = 30 ´ 8 _________________ -23x2 = -40
Ответ: Пример 2 Пусть имеются два пункта, расстояние между которыми равно 1000 км. Между ними необходимо осуществить связь, имеющую 12 телефонных, 31 телеграфных и 18 фототелеграфных каналов с помощью кабелей двух типов, обладающих следующими характеристиками:
Определить необходимое количество кабелей каждого типа для осуществления связи с наименьшими затратами. Решить задачу графически. Решение Введем переменные: x1 – количество кабеля типа I, x2 – количество кабеля типа II. По определению эти переменные должны быть неотрицательны. При связи, использующей x1 кабелей I типа и x2 кабелей II типа, могут использоваться x1+3x2 телефонных каналов, 5x1+4x2 телеграфных каналов и 2x1+3x2 фототелеграфных каналов. Для осуществления связи необходимо наличие не менее требуемого количества каналов. Получаем ограничения на количества имеющихся каналов:
Затраты на осуществление связи, имеющей x1 кабелей I типа и x2 кабелей II типа, составят: (12x1+16x2)×1000=12000x1+16000x2 условных единиц. Получаем математическую модель задачи:
Решим задачу графически. Каждое неравенство исходной системы ограничений определяет полуплоскость. Запишем уравнения граничных прямых для этих полуплоскостей.
Построим прямые. Каждая прямая разбивает плоскость на две полуплоскости. Для выбора полуплоскостей, определяемых каждым неравенством, подставим координаты «пробной» точки (0;0) в каждое неравенство. Получаем: 0 + 3 × 0 ³ 12 не верно. Следовательно, отмечаем полуплоскость, не содержащую «пробную» точку (0;0). 5 × 0 + 4 × 0 ³ 31 не верно. Следовательно, отмечаем полуплоскость, не содержащую «пробную» точку (0;0). 2 × 0 + 3 × 0 ³ 18 не верно. Следовательно, отмечаем полуплоскость, не содержащую «пробную» точку (0;0). Выбранные полуплоскости отметим стрелочками. Найдем пересечение отмеченных полуплоскостей с учетом условия: х1,х2³ 0. Заштрихуем полученный неограниченный четырехугольник ABCD. Построим линию уровня Z = 0: 12000х1 + 16000х2 = 0
Вектор Перемещая линию уровня параллельным переносом в направлении вектора
5х1 + 4х2 = 31´3 2х1 + 3х2 = 18´4 _________________ 7x1 = 21
Ответ: Для осуществления связи с наименьшими затратами необходимо 3 кабеля I типа и 4 кабеля II типа. При этом минимальные затраты составят 100 000 у.е. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 398. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
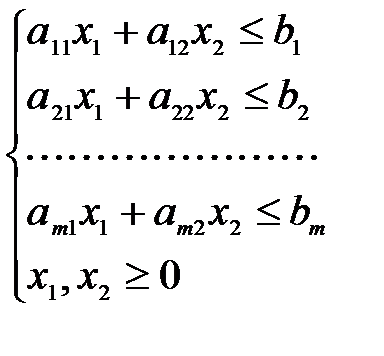

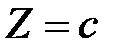 , где c – произвольная константа. В двумерном случае, это уравнение определяет прямую. Линии уровня образуют семейство параллельных прямых.
, где c – произвольная константа. В двумерном случае, это уравнение определяет прямую. Линии уровня образуют семейство параллельных прямых. называется градиентом функции Z. Вектор
называется градиентом функции Z. Вектор 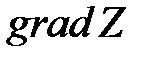 в каждой точке перпендикулярен линии уровня, проходящей через эту точку, и указывает направление наибольшего возрастания функции Z,
в каждой точке перпендикулярен линии уровня, проходящей через эту точку, и указывает направление наибольшего возрастания функции Z, 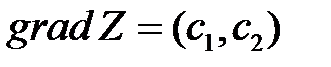 .
.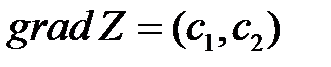 и одну из прямых семейства
и одну из прямых семейства  , то вместо него строят вектор
, то вместо него строят вектор 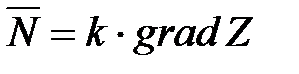 (в случае, если длина
(в случае, если длина  слишком мала для построения) или
слишком мала для построения) или  (в случае, если длина
(в случае, если длина  слишком велика для построения), где
слишком велика для построения), где  .
. .
. . Это будет наиболее удаленная вершина многоугольника, в которой линия уровня пересекается с многоугольником.
. Это будет наиболее удаленная вершина многоугольника, в которой линия уровня пересекается с многоугольником. (или перемещают в направлении
(или перемещают в направлении  при решении задачи линейного программирования возможны различные случаи. Рассмотрим их.
при решении задачи линейного программирования возможны различные случаи. Рассмотрим их.

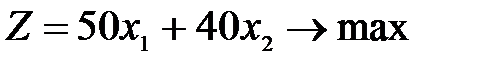

 определяет направление наибольшего возрастания функции Z. Построим из начала координат вектор
определяет направление наибольшего возрастания функции Z. Построим из начала координат вектор  . Этот вектор также показывает направление наибольшего возрастания функции.
. Этот вектор также показывает направление наибольшего возрастания функции.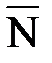 , находим последнюю точку пересечения линии уровня и заштрихованного пятиугольника – точку А. Эта точка является точкой максимума функции.
, находим последнюю точку пересечения линии уровня и заштрихованного пятиугольника – точку А. Эта точка является точкой максимума функции. –
–


 .
.
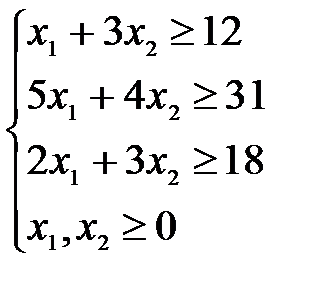


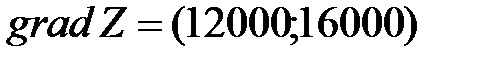 определяет направление наибольшего возрастания функции Z. Построим из начала координат вектор
определяет направление наибольшего возрастания функции Z. Построим из начала координат вектор  . Этот вектор также показывает направление наибольшего возрастания функции.
. Этот вектор также показывает направление наибольшего возрастания функции.
