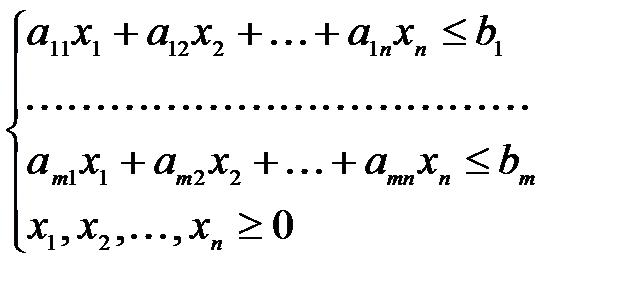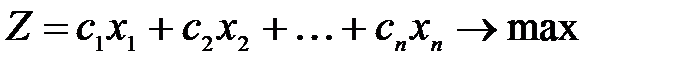Графический метод решения задачи линейного программирования

Графический метод применяется для решения ЗЛП, заданной в симметричной форме. Этот метод наиболее эффективно применяется для решения задач с двумя переменными, т.к. требует графических построений. В случае трех переменных необходимы построения в R³, в случае четырех переменных необходимы построения в R⁴ и т.д.

Множество точек называется выпуклым, если для любых двух точек множества оно содержит отрезок, их соединяющий.

Пример 1

Следующие множества точек на плоскости являются выпуклыми:

Следующие множества точек на плоскости не являются выпуклыми:

Теорема 1 Пересечение любого количества выпуклых множеств является выпуклым множеством.

Теорема 2 Пусть имеются две произвольные точки  и  в пространстве Rⁿ. Тогда для любой точки  отрезка [PQ] должно выполняться: .где .

Гиперплоскостью в пространстве Rⁿ называется множество точек, удовлетворяющее уравнению . Заметим, что в двумерном случае гиперплоскостью является прямая.

Полупространством называется множество точек, удовлетворяющее одному из неравенств  или . Гиперплоскость делит точки пространства на два полупространства. В двумерном случае гиперплоскостью является полуплоскость.

Теорема 3 Полупространство является выпуклым множеством.

Следствие Пересечение любого количества полупространств является выпуклым множеством.

Многогранником называется пересечение одного или более полупространств. Многогранник в двумерном случае называется многоугольником.

Пример 2

Следующие множества являются многоугольниками.

Точка выпуклого множества называется угловой, если она не лежит внутри никакого отрезка, соединяющего две другие точки из множества.

Пример 3

Угловыми точками треугольника являются его вершины (их три). Угловыми точками круга являются точки окружности, которая его ограничивает (их бесконечное число).

Угловая точка многогранника называется его вершиной.

Рассмотрим ЗЛП, заданную в симметричной форме.

Теорема 4 Оптимальный план ЗЛП соответствует вершине многогранника решений, определяемого ее системой ограничений.