
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Различные формы записи задачи линейного программирования.Стр 1 из 13Следующая ⇒ Методы оптимальных решений (Лекции)
2011 г. Введение. 3 1. Линейное программирование. 4 1.1. Различные формы записи задачи линейного программирования. 4 1.2. Графический метод решения задачи линейного программирования. 6 1.3. Графический способ метод решения ЗЛП, заданной в симметричной форме, в случае двух переменных. 8 1.4. Использование надстройки Поиск решения MSExcel 14 1.5. Решение ЗЛП средствами MSExcel. 18 1.6. Двойственные задачи. 21 Вопросы для самопроверки. 30 2. Специальные задачи линейного программирования. 31 2.1. Задача о назначениях. 31 2.2. Теория игр. 43 2.2.1. Основные понятия. 43 2.2.2. Нижняя и верхняя цены игры. Принцип минимакса. 45 2.2.3. Решение игр в смешанных стратегиях. 47 2.2.4. Решение матричных игр 2х2 в смешанных стратегиях. 48 2.2.5. Сведение матричной игры к задаче линейного программирования. 56 2.2.6. Игры с природой. 64 Вопросы для самопроверки. 69 3. Многоцелевые задачи. 69 3.1. Множество Парето. 70 3.2. Метод идеальной точки. 71 Вопросы для самопроверки. 77 4. Нелинейное программирование. 77 4.1. Графическое решение задачи нелинейного программирования. 78 4.2. Метод множителей Лагранжа. 80 4.3. Решение задач выпуклого программирования. 81 Вопросы для самопроверки. 88 Литература. 88 Введение Несмотря на многообразие задач организационного управления, при их решении можно выделить некоторую общую последовательность этапов, через которые проходит любое исследование. Как правило, это: 1.Постановка задачи. 2. Построение содержательной модели рассматриваемого объекта (процесса). На данном этапе происходит формализация цели управления объектом, выделение возможных управляющих воздействий, влияющих на достижение сформулированной цели, а также описание системы ограничений на управляющие воздействия.  3. Построение математической модели, т. е. перевод сконструированной модели в ту форму, в которой для ее изучения может быть использован математический аппарат. 4. Решение задач, сформулированных на базе построенной математической модели. 5. Проверка полученных результатов на их адекватность природе изучаемой системы, включая исследование влияния так называемых внемодельных факторов, и возможная корректировка первоначальной модели. 6. Реализация полученного решения на практике. В курсе методы оптимальных решений центральное место отведено вопросам, относящимся к четвертому пункту приведенной выше схемы. Это делается не потому, что он является самым важным, сложным или интересным, а потому, что остальные пункты существенно зависят от конкретной природы изучаемой системы, в силу чего для действий, которые должны производиться в их рамках, не могут быть сформулированы универсальные и содержательные рекомендации. Для решения экономической задачи математическими методами составляют математическую модель задачи, т.е. записывают ее с помощью математических выражений: неравенств, уравнений и т.п. Для математического описания экономической задачи можно руководствоваться следующей общей схемой: 1) выбирают некоторое количество переменных 2) выражают взаимосвязи исследуемого экономического процесса в виде математических соотношений (уравнений, неравенств). Эти соотношения образуют систему ограничений математической модели; 3) поиск наилучшего решения формулируют в терминах поиска оптимального (максимального или минимального) значения функции В зависимости от свойств целевой функции, математическое программирование можно рассматривать как ряд самостоятельных дисциплин, занимающихся изучением и разработкой методов решения определенных классов задач. Если Математическое моделирование является, с одной стороны, очень важным и сложным, а с другой — практически не поддающимся научной формализации процессом. Заметим, что неоднократно предпринимавшиеся попытки выделить общие принципы создания математических моделей приводили либо к декларированию рекомендаций самого общего характера, трудноприложимых для решения конкретных проблем, либо, наоборот, к появлению рецептов, применимых в действительности только к узкому кругу задач. Поэтому более полезным представляется знакомство с техникой математического моделирования на конкретных примерах. Мощным инструментом решения задач, построенных на базе математической модели, является наука, которая называется математическое программирование. В данном случае понятие программирование употребляется в смысле планирование (в отличие от программирования для ЭВМ). В свою очередь, в зависимости от вида решаемых задач, в математическом программировании выделяют такие области, как линейное, нелинейное, дискретное, динамическое, стохастическое программирование. Курс по методам оптимальных решений должен дать студентам достаточное представление о математическом аппарате, используемом при принятии решений в экономических задачах. Освоение этого материала придает студенту уверенность, которой обычно недостает, если он с самого начала направляет свои усилия на изучение философских аспектов и искусства принятия решений. Линейное программирование Различные формы записи задачи линейного программирования. Рассмотрим задачу линейного программирования (ЗЛП) в общем виде:
Задача линейного программирования задана в канонической форме, если требуется максимизировать целевую функцию, все ограничения системы – уравнения и на все переменные наложено условие неотрицательности. Задача линейного программирования задана в симметричной форме, если требуется максимизировать целевую функцию, все ограничения системы – неравенства «£» (или минимизировать целевую функцию, все ограничения системы– неравенства «³») и на все переменные наложено условие неотрицательности. Набор чисел Множество всех допустимых решений называется областью допустимых решений (ОДР). Допустимое решение Термины «план» и «оптимальный план» возникли из экономических приложений. Все три формы записи ЗЛП являются эквивалентными в том смысле, что имеются алгоритмы перехода от одной формы к другой. Таким образом, если имеется способ решения задачи в одной из форм, то всегда можно определить оптимальный план задачи, заданной в любой другой форме. Задача в симметричной форме решается графическим методом, а в канонической форме – симплекс–методом. Рассмотрим алгоритмы перехода от одной формы к другой. · Симметричная ® каноническая. Переход осуществляется путем добавления в левую часть каждого неравенства дополнительной неотрицательной переменной. Если неравенство было «≤», то балансовая переменная добавляется в левую часть неравенства со знаком «+». Если неравенство было «³», то балансовая переменная добавляется в левую часть неравенства со знаком «–». Вводимые новые переменные называются балансовыми. Задачу минимизации функции Z заменяют на задачу максимизации функции (–Z) и используют, что min Z = –max (–Z). · Каноническая ® симметричная. Для осуществления такого перехода находится общее решение системы уравнений – ограничений, целевая функция выражается через свободные переменные. Далее, воспользовавшись неотрицательностью базисных переменных, можно исключить их из задачи. Симметричная форма задачи будет содержать неравенства, связывающие только свободные переменные, и целевую функцию, зависящую только от свободных переменных. Значения базисных переменных находятся из общего решения исходной системы уравнений. · Общая ® каноническая. Каждая переменная, на которую не было наложено условие неотрицательности, представляется в виде разности двух новых неотрицательных переменных. Неравенства преобразуются в уравнения путем введения в левую часть каждого неравенства балансовой переменной таким же образом, как это было описано при переходе от симметричной к канонической форме. Задачу минимизации функции Z заменяют на задачу максимизации функции (–Z) таким же образом, как это было описано при переходе от симметричной к канонической форме.. |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 374. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , заданием числовых значений которых однозначно определяется одно из возможных состояний исследуемого экономического процесса;
, заданием числовых значений которых однозначно определяется одно из возможных состояний исследуемого экономического процесса;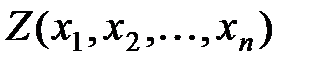 . Построенная функция называется целевой.
. Построенная функция называется целевой. - линейная функция и линейны функции, описывающие ограничения на переменные
- линейная функция и линейны функции, описывающие ограничения на переменные  , то математическая модель представляет задачу линейного программирования. Если хотя бы одна из указанных функций нелинейная, то математическая модель является объектом исследования нелинейного программирования. Наиболее изученным разделом математического программирования является линейное программирование. Для решения задач этого раздела разработан целый ряд эффективных алгоритмов и методов.
, то математическая модель представляет задачу линейного программирования. Если хотя бы одна из указанных функций нелинейная, то математическая модель является объектом исследования нелинейного программирования. Наиболее изученным разделом математического программирования является линейное программирование. Для решения задач этого раздела разработан целый ряд эффективных алгоритмов и методов.

 называется допустимым решением (планом), если он удовлетворяет системе ограничений ЗЛП.
называется допустимым решением (планом), если он удовлетворяет системе ограничений ЗЛП. , для которого достигается максимальное (минимальное) значение функции, называется оптимальным планом ЗЛП.
, для которого достигается максимальное (минимальное) значение функции, называется оптимальным планом ЗЛП.