
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Лінії току при довільному ударі пластини ⇐ ПредыдущаяСтр 8 из 8 Перепишемо формулу (53) у наступному вигляді:
Поле швидкостей при довільному ударі горизонтальної пластинки може бутиотримано зі співвідношення
Функція току у безрозмірномувиглядінаграницітечіїмаєвигляд:
Рис. 17. Величина функції току на вісі х.
При наближенні
На приведеному малюнку зображений графік функції Значення функції токадва рази покривають інтервал від свого мінімального значення
Відмітимо ще дві характерні точки Отже, усі лінії току будуть починатися на поверхні пластини у частині області безвідривного обтікання при  При значенні кінематичного параметру
Картина ліній токупри
Рис. 18. Лінії току при довільному обтіканні пластини рідиною.
V. Висновки
Розглянуто задачу про удар пластини по вільній поверхніідеальноїнестисливої рідини, яка знаходиться у станіспокою, з різними граничними умовами. Було знайдено поле комплексної імпульсної швидкості рідини внаслідок удару у мить часу, що слідує безпосередньо за миттю удару. За допомогою зведення гідродинамічної задачі до змішаної задачі Келдиша-Сєдова отримано точний аналітичний розв’язок. Отримано вирази длякомпонент швидкості рідини,вирази для імпульсної сили та моменту, що діють на тіло у формі пластини як у випадку безвідривного, так і відривного обтікання. Зроблено аналіз результатів та побудовано графіки, що ілюструють гідродинамічні параметри на поверхні рідини, а також побудовано картина ліній току при відривній течії. Виходячи з отриманих результатів, можна зауважити, що отримані силові фактори, що діють на пластину з боку рідини у мить удару, є нелінійними характеристиками від поступальної та обертальної швидкості, оскільки точка відриву залежить від кінематичного параметру, який характеризує зв’язокміж зазначеними вище поступальною та обертальною швидкістю. Список літератури
Російською: 1. Кочин Н.Е.,Кибель И.А., РозеН.В. – Теоретическаягидромеханика. – М.: Гостехиздат, 1948. – 536с. 2. Седов Л.И. – Плоскиезадачигидродинамики и аэродинамики. – М.: Наука, 1966. – 448с. 3. Лаврентьев М.А., Шабат Б.В. – Методытеориифункций комплексного переменного. – М.: Наука,1973. – 736с. 4. Лойцянский Л. Г. – Механикажидкости и газа. – М.: Наука, 1970. – 904с. 5. Мусхелишвилли Н.И. – Сингулярныеинтегральныеуравнения. – М.:Наука, 1968. – 512с. 6. Гуревич М.И. – Теорияструйидеальнойжидкости. – М.: Государственноеиздательствофизико-математическойлитературы, 1961. – 496с. 7. Норкин М.В. – Смешанные задачигидродинамическогоудара. – Ростов-на-Дону: Южныйфедеральный университет, 2007. – 136с. 8.. Гоман О. Г., Катан В. А. Ударноевзаимодействиенесжимаемойжидкости и вертикальнойпластины, плавающей на ееповерхности, в условияхобразованияоднойзоныотрыва и налички вращения // Вісник Дніпропетровського університету. Серія «Механіка», 2013, Вик. 17, т. 1. – с. 191-205.
|
||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 372. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
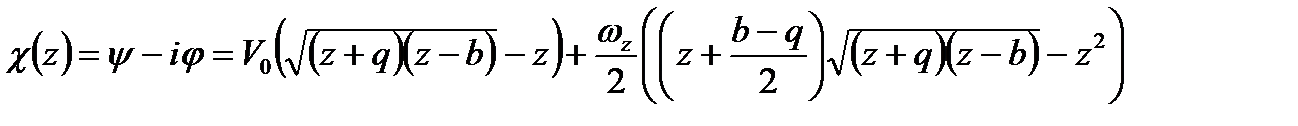 .(76)
.(76) . (77)
. (77) Тут λ – точка відриву. Характерний вигляд залежності функції току від координати на границі течії при
Тут λ – точка відриву. Характерний вигляд залежності функції току від координати на границі течії при  , показано на рисунку 17.
, показано на рисунку 17.
 функція токунаближується до однієї границі, що дорівнює
функція токунаближується до однієї границі, що дорівнює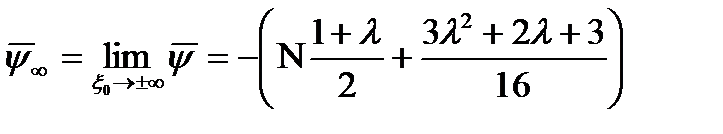 .
. , тому на нескінченності вказана функція прямує до нуля.
, тому на нескінченності вказана функція прямує до нуля. до її максимально значення
до її максимально значення  , окрім
, окрім  . Значення
. Значення  .
. та
та  . В точці з координатою
. В точці з координатою 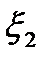 значення функції співпадає з її значенням в точці
значення функції співпадає з її значенням в точці  . В точці
. В точці 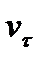 дорівнює нулю та імпульсивний тиск приймає максимальне значення, а лінія току в цій точці перпендикулярна до границі течії, тобто до поверхні пластини. Також на ділянках вільної поверхні й у відривній зоні, лінії току перпендикулярні до кордону течії. На проміжку
дорівнює нулю та імпульсивний тиск приймає максимальне значення, а лінія току в цій точці перпендикулярна до границі течії, тобто до поверхні пластини. Також на ділянках вільної поверхні й у відривній зоні, лінії току перпендикулярні до кордону течії. На проміжку  дотична швидкість
дотична швидкість  має додатній знак, а на ділянці
має додатній знак, а на ділянці  вона від’ємна.
вона від’ємна. . Лінії току з проміжку
. Лінії току з проміжку 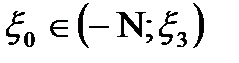 будуть закінчуватися в області безвідривної течії на проміжку
будуть закінчуватися в області безвідривної течії на проміжку  . Лінії току з проміжку
. Лінії току з проміжку  закінчуються у зоні відриву та на вільній поверхні
закінчуються у зоні відриву та на вільній поверхні  . Лінія току, що виходить з точки
. Лінія току, що виходить з точки  , прямує до нескінченності. Лінії току з проміжку
, прямує до нескінченності. Лінії току з проміжку  закінчуються на вільній поверхні
закінчуються на вільній поверхні  .
.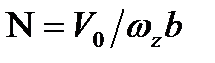 , = 0.25, значення координат критичних точок наступні:
, = 0.25, значення координат критичних точок наступні:




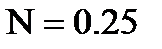 подана на рисунку 18.
подана на рисунку 18.