Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Постановка задачі про удар пластини об поверхню рідини, що заповнює нижній на півпростір
Нехай область, що зайнята рідиною, являє собою півпростір, тобто можемо вважати, що границі басейну знаходяться достатньо далеко, що можемо знехтувати їх впливом на пластинку. На вільній границі у контакті з рідиною знаходиться плоска пластина. У мить удару пластина отримуєвертикальну поступальну та обертову швидкість. На вільній поверхні рідини горизонтальна компонента швидкості дорівнює нулю.В залежності від того, якими будуть швидкості, що отримала пластина, обтікання може виникнути як з відривом від поверхні пластини, так і без нього. Розглянемо обидва випадки.
Безвідривне обтікання Розглянемо випадок, коли рідина обтікає пластину безвідривно та область
Рис. 2. Схема обтікання без відриву.
Задача, що розглядається, являє собою змішану задачу для напівплощини, аналогічна задачі Келдиша та Седова, тому їїрішення будемо шукати як:
де
В області
У якості R(z), спираючись на формулу (13) беремо таку функцію:
В області
Підставивши (27) та (26) у (25), функція
Розіб’ємо цю функцію на два доданки та розглянемо окремо два інтеграли:
 Обчислимо їх як інтеграли типу Коші. Візьмемодвузв’язну область з внутрішнім контуромL, та зовнішнім L1. Внутрішній контур Lспрямуємо до розрізу[-b;b], зовнiшнійконтур L1 спрямуємо у нескінченність(рис. 3).
Введемо функцію
розкладемо у ряд та візьмемо перші два члени:
Перенесемо перші два члени у ліву частину. Отримана функція буде прямувати до нуля порядку
Обчислимо інтеграли типу Коші від цієї функції:
Перший інтеграл буде прямувати до нуля, коли зовнішній контур прямує до нескінченності. Другий обчислимо як інтеграл за верхнім та нижнім берегом розрізу [-b;b] . Отримаємо:
де
Підставляючи (31) в (30), отримаємо:
Формула (32) є інтегралом I1 з формули (29), поділеним на π. З іншого боку:
Отже, маємо, що шуканий нами інтеграл
Аналогічні дії зробимо, розглядаючи другий інтеграл з (29), та будемо мати, що
Підставимо (34) та (35) у вираз для поля комплексноїшвидкості (28).
або ж
Отже, поле комплексноїшвидкості рідини знайдено. Задовольнимо тепер граничним умовам (1) і (2). В області D1: Поле швидкості рідини має вигляд:
а її компоненти дорівнюють:
В області D2. 1) Якщо
компоненти швидкості будуть такими:
2) Якщо
а компоненти швидкості будуть такими:
Бачимо, що граничні умови задовільнені, отже, поле швидкостей знайдено вірно. Знайдемо тепер комплексний потенціал рідини w, який обчислюється за формулою
Отже, будемо мати:
або ж, обчисливши інтеграл
Знайдемо комплексний потенціал w та потенціал швидкості φ на осі Ох. 1) При
2) При
3) При
Імпульс сил, що діє на поверхню рідини:
А сумарний вектор сил
Обчисливши інтеграли, отримаємо:
Відривне обтікання Розглянемо тепер випадок, коли кутова швидкість настількі велика, що виникає відрив рідини від пластини у точці –q(рис. 3).
Рис. 4. Схема обтікання звідривом
У цьому разі у формулі (25) в якості R(z) слід взяти функцію
а область D2 з формули (26) буде займати частину вісі Ох [-q;b]. Отже, поле швидкості будемо шукати за такою формулою:
Розіб’ємо цю функцію на два доданки та розглянемо окремо два інтеграли:
Проведемо міркування аналогічно як для обчислення інтегралів з формул (29). Однак в цьому випадку контур L лягатиме на розріз [-q;b].Після обчислення отримаємо, що
Тоді, підставивши (43) та (44) в (41)поле швидкості отримаємо у наступному вигляді:
Таким чином, знайшовши поле швидкості, знайдемо компоненти швидкості на вісі Ох. В області D2.
В області D1. 1) Якщо
2)Якщо
Бачимо, що граничні умови задовільнено, іполе швидкості знайдено вірно. Знайдемо тепер комплексний потенціал рідини w, який обчислюється за формулою
Отже, будемо мати:
або ж, обчисливши інтеграл
Знайдемо тепер комплексний потенціал w та потенціал швидкості φ на осі Ох. 1) При
2) При
3) При
Імпульс сил, що діє на поверхню рідини:
А сумарний вектор сил
Обчисливши інтеграли, отримаємо:
Знайдемо тепер точку відриву -q та при яких кутових швидкостях буде виникати відрив рідини від пластини. На пластині в точці –q виконується умова, що
Отже, з виразу поля швидкості (42) при
Цей вираз буде вірним, коли виконується умова
або ж, спростивши
Введемо безрозмірні величини
та представимо вираз (49) у безрозмірних величинах
Знайдемо залежність
Рішення
або ж
Знайдемо критичні значення 1) при 2) при 3) при Отже, відривне обтікання виникає при умові
За отриманою величиною Поле швидкості буде таким
Компоненти швидкості на вісі Ох приймуть наступний вигляд. В області D2.
В області D1. 1) Якщо
2)Якщо
Комплексний потенціал рідини матиме такий вигляд:
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 319. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 являє собою проміжок
являє собою проміжок  (рис. 2).
(рис. 2).
 (25)
(25) – граничні умови, які мають вигляд
– граничні умови, які мають вигляд (26)
(26) цей інтеграл буде дорівнювати нулю за умовами (26), тому інтегрувати будемо тільки за проміжком [
цей інтеграл буде дорівнювати нулю за умовами (26), тому інтегрувати будемо тільки за проміжком [  ]. Отже, маємо:
]. Отже, маємо:

 , тому функція
, тому функція 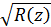 приймає вигляд
приймає вигляд (27)
(27)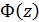 приймає такий вигляд:
приймає такий вигляд: (28)
(28) (29)
(29)
 .Представимо її у вигляді
.Представимо її у вигляді
 .
. , коли z прямує до нескінченності. Ліва частина буде мати вигляд:
, коли z прямує до нескінченності. Ліва частина буде мати вигляд: .
. .
.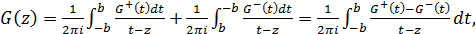 (30)
(30)
 (31)
(31) . (32)
. (32) . (33)
. (33)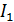 дорівнює
дорівнює . (34)
. (34) . (35)
. (35)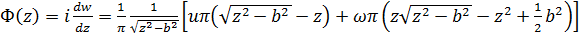 ,
, . (36)
. (36) .
. ,
, ;
; .
. , тоді поле швидкості рідини має вигляд:
, тоді поле швидкості рідини має вигляд:

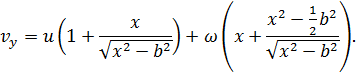
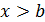 , тоді поле швидкості рідини має вигляд:
, тоді поле швидкості рідини має вигляд:

 .
.




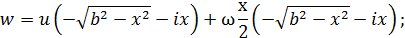


 та сумарний момент
та сумарний момент 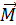 , які діють на рідину, матимуть вигляд:
, які діють на рідину, матимуть вигляд: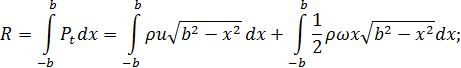




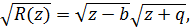 (40)
(40) (41)
(41) (42)
(42)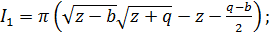 (43)
(43) (44)
(44)














 та сумарний момент
та сумарний момент  , які діють на рідину, матимуть вигляд:
, які діють на рідину, матимуть вигляд: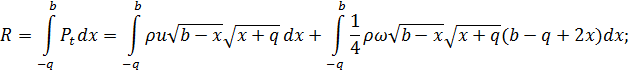
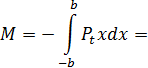
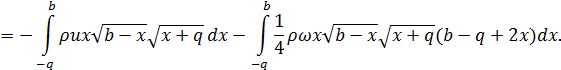



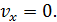
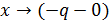 будемо мати границю
будемо мати границю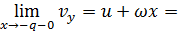

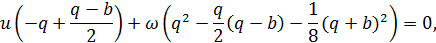
 (49)
(49)

 :
:

 не належить області значень, тому його виключаємо з розгляду. Отже, остаточноотримаємо:
не належить області значень, тому його виключаємо з розгляду. Отже, остаточноотримаємо:

 , за якої виникає відрівне обтікання:
, за якої виникає відрівне обтікання: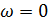 :
: 
 :
: 
 :
: