
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Змішана задача длянапівплощини. Формули Келдиша-СєдоваНехай на дійсній осі Ох дана система роздільнихвідрізків Змішану задачу у нашому випадку формулюємо так: знайти функцію
Ми вважаємо, що поблизу Розв’язок цієї задачі можна відразу отримати шляхом перетворення за допомогою дробово-лінійної підстановки Однорідна задача спряження, відповідна нашій задачі має вигляд
причому потрібно знайти рішення, що володіють властивістю Зарозв'язок цієї однорідної задачівізьмемо функцію
де
Під
Це рівнозначно тому, що Легко побачити, що
де C0,…Cp – довільно дійсні постійні. Знайдемо тепер канонічне рішення Z задачі (11). Таким рішенням буде з точністю до постійного множника 
де
А під
Один з частинних розв’язків
де
А під Загальне рішення вихідної задачі дається, таким чином, формулою
де С – дійсна довільна постійна. Отримані в цьому параграфі формули являють собою формули М.В. Келдиша і Л.І.Седова.
Інтеграл типу Коші
Вираз
де f(z) – aналітична функція на замкнутій області Якщо Нехай тепер L – будь-яка кусково гладка орієнтована крива. Не обов'язково замкнута, і є інтегралом типу Коші. Формула (21) являє собою функцію Справедлива така теорема. Інтеграл типу Коші є аналітична функція для всіх
Доказ.Нехай σ є довільне коло, що не має спільних точок з кривою L. Функція двох комплексних змінних z та z0
неперервна на множині
Це дає змогу бачити, що диференціювання При цьому похідна Ми довели формулу (22) у разі n = 1. Для n>=2 міркування ведуться за індукцією. Слідство: Якщо функція аналітична в області D, тобто має безперервну першу похідну на, то вона має похідні всіх порядків. Доказ: Нехай
тобто функція
ІІ. Постановка задачi Розглядається задача про удар тіла по вільній поверхні нестисливої рідини, яка знаходиться у басейні . Припускається, що на поверхні рідини, яка знаходиться у стані спокою, плаває тверде тіло (або тіла), на яке у певний момент часу діє імпульсна сила та імпульсний момент. Ці силові фактори призводять до виникнення миттєвої поступальної швидкості та кутової швидкості тіла, завдяки чому миттєво виникає поле швидкості рідини. Гідродинамічна задача полягає у визначенні поля швидкості рідини та інших гідродинамічних параметрів, якщо відома форма поверхні тіла та басейну, а також миттєва швидкість тіла і кутова швидкість після імпульсивної (ударної) дії. В роботі розглядається задача у плоскій постановці, вважається, що на поверхні рідини плаває пластинка чи платинки (або до поверхні рідини впритул дотикається тіло своїм плоским торцем ), яка внаслідок дії імпульсу отримує вертикальну швидкість Виберемо систему координат Oxy, направивши вісь у вглиб рідини, перпендикулярно до площини вільної поверхні, вісь х направимо вздовж цієї поверхні (рис. 1).
Рис. 1. Схема до постановки задачі.
Таким чином, внаслідок удару елементи поверхні пластини миттєво отримують вертикальну складову швидкості
і задача полягає у визначенні поля швидкості рідини, яке визвано вказаним рухом поверхні пластинки. Позначимо через D1 частину осі Ох, що являє собою слід пластини на площині, через D2 – частину осі, що займає вільна поверхня рідини, а через D3 – границі басейну. Задача полягає узнаходженні поля швидкостей рідини у мить, що слідує безпосередньо за ударом, та інших гідродинамічних параметрів. Потрібно знайти функцію
Знайшовши поле швидкостей, обчислимо комплексний потенціал та знайдемо гідродинамічні параметри.
ІII. Розв'язання
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 348. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
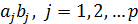 (мається на увазі, що
(мається на увазі, що 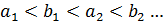 ). Позначимо через
). Позначимо через 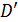 сукупність цих відрізків, а через
сукупність цих відрізків, а через 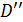 – решту дійсної осі, так що
– решту дійсної осі, так що 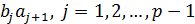 з нескінченного «відрізка», що складається з двох напівпрямих
з нескінченного «відрізка», що складається з двох напівпрямих 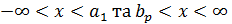 .
.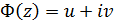 , голоморфну на верхній напівплощині
, голоморфну на верхній напівплощині 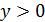 та обмежену у нескінченності, за граничними умовами:
та обмежену у нескінченності, за граничними умовами: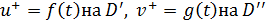 (10)
(10)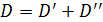 (так ми позначаємо всю дійсну вісь), задані функції
(так ми позначаємо всю дійсну вісь), задані функції 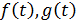 задовольняють умовiГельдера (умові Н)
задовольняють умовiГельдера (умові Н) 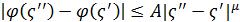 відповідно на
відповідно на 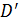 i
i 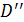 , включаючи нескінченно віддалену точку.
, включаючи нескінченно віддалену точку.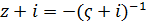 .Ми, однак, отримаємо більш простий результат трохи іншим способом.
.Ми, однак, отримаємо більш простий результат трохи іншим способом.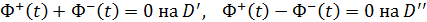 (11)
(11)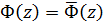 , де
, де 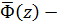 функція, спряжена з функцією
функція, спряжена з функцією 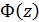 .
.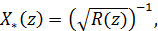 (12)
(12)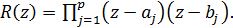 (13)
(13)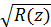 мається на увазі гілка, голоморфна на розрізаної вздовж D’ площині і така, що поблизу
мається на увазі гілка, голоморфна на розрізаної вздовж D’ площині і така, що поблизу 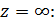
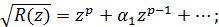 (14)
(14)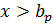 .
.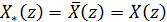 . Загальне рішення однорідної задачі, що виходитьз (10) при f(t)=g(t)=0 дається формулою
. Загальне рішення однорідної задачі, що виходитьз (10) при f(t)=g(t)=0 дається формулою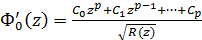 , (15)
, (15)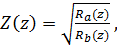 (16)
(16)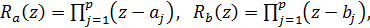 (17)
(17)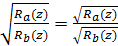 мається на увазі гілка,голоморфна на розрізаної вздовж осі D’ площині, приймаюча на нескінченності значення 1. І в цьому випадку
мається на увазі гілка,голоморфна на розрізаної вздовж осі D’ площині, приймаюча на нескінченності значення 1. І в цьому випадку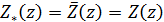 .
. вихідної задачі дається формулою
вихідної задачі дається формулою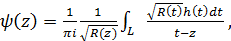 (18)
(18)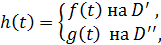 (19)
(19)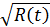 розуміється значення, яке приймається
розуміється значення, яке приймається 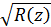 при z→t на верхній півплощині.
при z→t на верхній півплощині.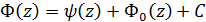 , (18)
, (18)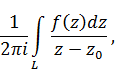
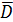 , що обмеженадодатньо орієнтованим контуром L, називається інтегралом Коші.
, що обмеженадодатньо орієнтованим контуром L, називається інтегралом Коші.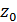 лежить всередині L, то інтеграл дорівнює
лежить всередині L, то інтеграл дорівнює 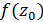 , якщо ж
, якщо ж 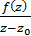 аналітична і, отже, інтеграл Kоші дорівнює нулю.
аналітична і, отже, інтеграл Kоші дорівнює нулю.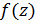 – безперервна функція, визначена вздовж L. Тоді вираз
– безперервна функція, визначена вздовж L. Тоді вираз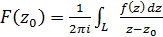 (21)
(21)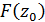 , визначену поза L.
, визначену поза L.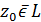 . Похідна порядкуn від
. Похідна порядкуn від 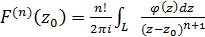 . (22)
. (22)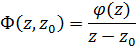
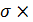 Lі має на ньому безперервну частинну похідну
Lі має на ньому безперервну частинну похідну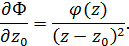
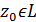 та
та 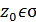 різниця
різниця 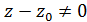 ).
).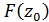 за параметром
за параметром 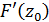 неперервна поза L. Але тоді
неперервна поза L. Але тоді 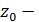 будь-яка точка D,
будь-яка точка D, 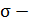 коло з центром в
коло з центром в 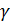 – границя
– границя 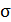 , спрямована проти годинникової стрілки. Тоді за формулою Коші
, спрямована проти годинникової стрілки. Тоді за формулою Коші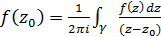 , (23)
, (23)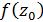 зображується інтегралом типу Коші при L=
зображується інтегралом типу Коші при L= 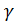 та
та 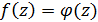 . Отже, в силу теореми,
. Отже, в силу теореми, 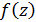 нескінченно диференційовна та
нескінченно диференційовна та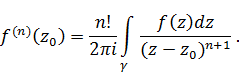
 , перпендикулярну до площини вільної поверхні рідини, та кутову швидкість обертання ω навколо вісі, що лежить у площині вільної поверхні.
, перпендикулярну до площини вільної поверхні рідини, та кутову швидкість обертання ω навколо вісі, що лежить у площині вільної поверхні.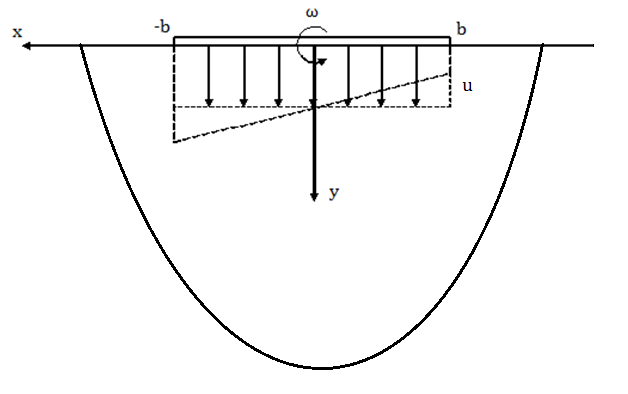
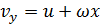
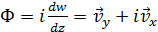 ,голоморфнув області, що займає рідина, та обмежену на нескінченності, за такими граничними умовами:
,голоморфнув області, що займає рідина, та обмежену на нескінченності, за такими граничними умовами: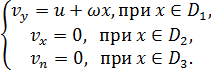 (24)
(24)