Удар двох пластин обграницюнапівплощини

Розглянемо задачу про одночасний удар декількох пластин об вільну поверхню рідини. Для певності розглянемо випадок, коли на вільній поверхні рідини, яку вважаємо безмежною вглиб та вбоки, лежать дві пластини. У деяку мить часу на пластини діють імпульсні сили, в результаті яких кожна пластина отримує певну вертикальну поступальну та обертову швидкість. На вільній поверхні рідини горизонтальна складова швидкості буде нульовою. Систему координат виберемо так, щобвісь хбула спрямована вздовж вільної поверхні рідини, а вісь унаправлена вертикально вглиб.Рідину вважаємо ідеальною та нестисливою. Позначимо через область D₁ частину вісі х, на яких лежать пластини, тобто а через D₂– іншу частину вісі.

У такій постановці будемо мати наступні граничні умови:

Рис. 5. Схема до постановки задачі.

Задача зводиться до знаходження комплексного потенціалу в області течії рідини зі змішаними граничними умовами.

Розглянемо функцію . Будемо знаходити її за допомогою інтегралу Келдиша-Сєдова.

Де h(t) має наступний вигляд:

В якостi R(z) вiзьмемофункцію

Розглянемо цю функцiю на рiзнихдiлянкахграницi.

1)x<a₁, y=0

2) a₁<x<b₁, y=0

3) b₁<x<a₂, y=0

4) a₂<x< b₂, y=0

5) b₂<x, y=0

Пiдставимо(56) та (57)доiнтегралуКелдиша-Сєдова (55) :

Перевiримо виконання граничних умов на дiлянках (a₁; b₁) та(a₂; b₂). За формулою Сохоцького для інтеграла

при наближеннi до лiвого берега дiлянкиiнтегрування матимемо:

де останнiйiнтегралрозумiється у сенсi головного значення по Кошi таким чином:

Отже, при наближеннi до дiлянки(a₂; b₂) зверху (y>0) отримаємо, що перший iнтеграл в (58) залишається без змiн, а другий зазнає перетворень за формулою Сохоцького:

Позначимо в (59) перший iнтеграл як I₂₁, а другий як I₂₂. IнтегралI₂₁– звичайний, а I₂₂–iнтеграл у сенсi головного значення Кошi.

У результатi отримаємо, що на дiлянцi(a₂; b₂)

Звiдси бачимо, що гранична умова виконується, а для дотичної компоненти швидкостi напластинці (a₂; b₂) маємо вираз:

Тепер розглянемо дiлянку(a₁; b₁). Зробимо аналогiчнiдiї та на цiйдiлянцi матимемо:

Позначимо перший інтегралв (61) I₁₁, а другий як I₁₂.Тут iнтеграл I₁₁–особливий у головному сенсiКошi.

Бачимо, що тут також задовільнено граничним умовам, а вираз для дотичної компоненти швидкості на (a₁; b₁) буде таким:

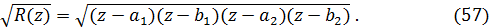
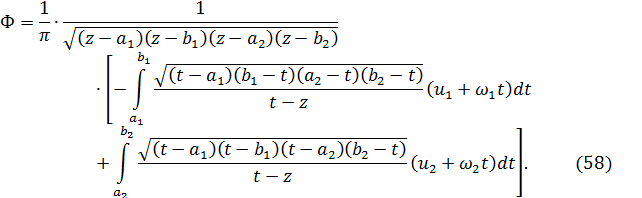
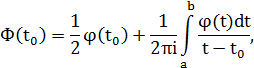
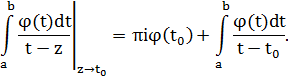
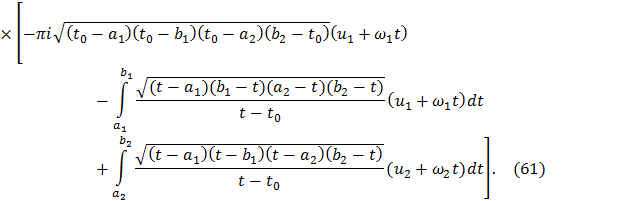
Імпульсивний тиск  тому для визначення розподілу імпульсів по пластині потрібно визначити потенціал 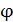 шляхом інтегрування. Потенціал є неперервною функцією, при чому на вільній поверхні він, за визначенням, дорівнює нулю.