
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Постановка задачi про удар об поверхнюрiдини, щозаповнюєпрямокутнийбасейннескiнченноїглибиниНехай область, що зайнята рідиною, представляє собою напівсмугу шириною h, що з боків обмежена твердими границями та необмежена вглиб. Систему координат оберемо так, що вісь у направлена вглиб рідини вздовж однієї з твердих границь, а вісь х направлена вздовж вільної границі рідини. На вільній границі у контакті з рідиною знаходиться плоска пластина. У мить удару пластина отримує вертикальну поступальну та обертову швидкість. На вільній поверхні рідини горизонтальна компонента швидкості дорівнює нулю, на твердих границях нормальна компонента швидкості також дорівнює нулю. Матимемо такі граничні умови:
Рис. 8. Схема до постановки задачі.
Щобзвестицю задачу до задачіКелдиша-Сєдова, зробимоконформне відображення, яке переводить напівсмугу у напівплощину. Для цього скористаємося інтегралом Шварца-Крістоффеля. Вимагатимемо, щоб три певні точки з площини z переходили у певні точки площини t наступним чином:
При чому граничні умови перейдуть у такі:
Рис. 9. Схема конформного відображення.
Отже, матимемо відображення:
або, підставивши значення координат
Обчислившиінтеграл,матимемо наступне:
Сталі інтегрування знаходимо з умови відповідності вказаних точок площини zтаплощиниt:
Отже, матимемо відображення:
Звідси бачимо, що при
Виразивши tчерез z, отримаємо зворотнє відображення:
Функція (68) на ділянці пластини, тобто на 
Введемо як завжди функцію
а також функцію
Тепер розглянемо функцію (71) на кожній ділянці вісі
1)
2)
3)
Отже, теперможемо записати формулуКелдиша-Сєдова:
Вираз (73) являє собою рішення розглянутої задачі. Перейдемо до розгляду цього виразу на ділянці, яку займає пластина. Таким чином, матимемо вираз
Перевіримо, чи задовольняється гранична умова на пластинці, тобто на ділянці
Підставимоостанній вираз до формули Келдиша-Сєдова:
Бачимо, що граничні умови задовольняються, а вертикальна та горизонтальна компонента швидкості на пластинці, як функції змінної
при цьому зв'язок фізичної координати
Імпульсивний тиск
IV. Результати
Було розглянуто задачу про удар плоскої пластини об вільну поверхню рідини з утворенням зони відриву у декількох постановках. Зокрема, про: 1) удар пластини о вільну поверхню рідини, коли рідина займає півпростір; 2) удар двох пластин о вільну поверхню рідини, коли рідина займає півпростір; 3) удар пластини о вільну поверхню шару рідини, що обмежений плоским дном; 4) удар пластини об поверхню рiдини, що заповнює прямокутний басейн нескiнченної глибини. В усіх розглянутих випадках вдалося знайти аналітичні вирази для комплексних потенціалів рідини. Були знайдені також вирази для компонент швидкості на ділянці, що займає пластина. Проілюструємо результати на прикладі удару пластинио рідину, що займає півпростір.
Безвідривне обтікання
Візьмемо для розгляду пластину шириною Розглянемо, якими будуть компоненти швидкості при безвідривному обтіканні. На рисунку 10 представлено розподіл вертикальної компоненти швидкості вздовж поверхні рідини. Із розгляду виключені точки
Рис. 10. Компонента швидкості vy при безвідривному обтіканні.
На рисунку11 представлено розподіл горизонтальної компоненти швидкості вздовж поверхні рідини. Із розгляду також виключені точки
Рис. 11. Компонента швидкості vx при безвідривному обтіканні.
Розподіл імпульсноготиску по пластині матиме вигляд, який показано на рисунку 12. Максимуму функція тиску досягає в точці
Рис. 12. Розподіл імпульсноготиску при безвідривному обтіканні. Відривнеобтікання
Якщо кутову швидкість збільшити до деякої величини, то виникне відрив рідини від пластини. У цьому випадку буде мати місце відривне обтікання. Як було розраховано, відрив виникає за кутової швидкості На рисунку 13 представлено функцію вертикальної компоненти швидкості на вільній поверхні рідини, що займає верхній півпростір. Можна побачити, що в точці
Рис. 13. Компонента швидкості vy привідривному обтіканні.
На рисунку14 представлено розподіл горизонтальної компоненти швидкості вздовж поверхні рідини при відривному обтіканні. Бачимо, що в точках
Рис. 14. Компонента швидкості vх привідривному обтіканні. Проілюструємо, як виглядатиме розподіл імпульсного тиску з боку рідини по пластині в залежності від положення точки відриву. З рисунка 15 видно, щона кінці пластини та в точці відриву імпульсний тиск дорівнює нулю.
Рис. 15. Розподіл імпульсного тиску по пластині при різних положеннях точки відриву.
На рисунку 16 зображено розподіл сумарної імпульсної сили, що діє на пластину з боку рідини, в залежності від положення точки відриву. Точка
Рис. 16. Залежність величини сумарної імпульсної сили від положення точки відриву.
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 307. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |



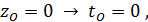


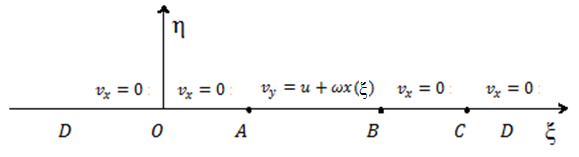

 і
і  :
:



 ділянка
ділянка  переходить у ділянку CD :
переходить у ділянку CD :  , а ділянка
, а ділянка  переходить у ділянку
переходить у ділянку  . За допомогою формули (68) можемо визначити, куди переходять точки А та В, а саме:
. За допомогою формули (68) можемо визначити, куди переходять точки А та В, а саме: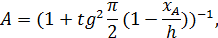


 прийме наступний вигляд
прийме наступний вигляд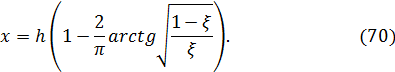



 .
.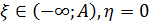 :
:
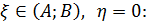




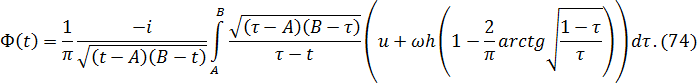
 зверху за формулою маємо:
зверху за формулою маємо: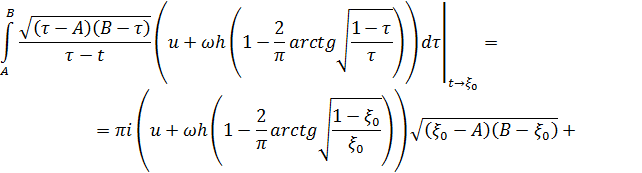



 , приймуть вигляд:
, приймуть вигляд:
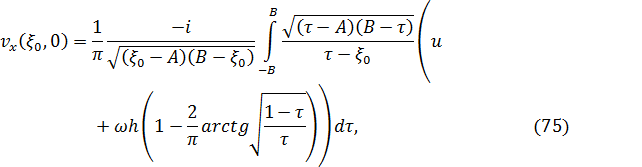
 з допоміжною координатою
з допоміжною координатою 
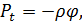 тому для обчислення імпульсів на пластині потрібно визначити потенціал
тому для обчислення імпульсів на пластині потрібно визначити потенціал 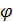 шляхом інтегрування виразу (75).
шляхом інтегрування виразу (75).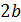 з параметрами
з параметрами 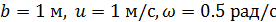 .
. та
та 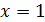 , бо в них функція приймає нескінченні значення.Легко побачити, що біля кінців пластини рідина має нескінченні швидкості а по віддаленні від пластини швидкість прямує до нуля.
, бо в них функція приймає нескінченні значення.Легко побачити, що біля кінців пластини рідина має нескінченні швидкості а по віддаленні від пластини швидкість прямує до нуля.
 . Можемо побачити, що вздовж вільної поверхні горизонтальна компонента швидкості дорівнює нулю.
. Можемо побачити, що вздовж вільної поверхні горизонтальна компонента швидкості дорівнює нулю.
 , та в даному випадку
, та в даному випадку  .Накінцяхпластини функція дорівнює нулю.
.Накінцяхпластини функція дорівнює нулю.
 . Для розрахунків візьмемо
. Для розрахунків візьмемо  .
.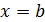 рідина має нескінченну швидкість, а за умови
рідина має нескінченну швидкість, а за умови  в точці
в точці  виникаєвідрив.
виникаєвідрив.
 та
та 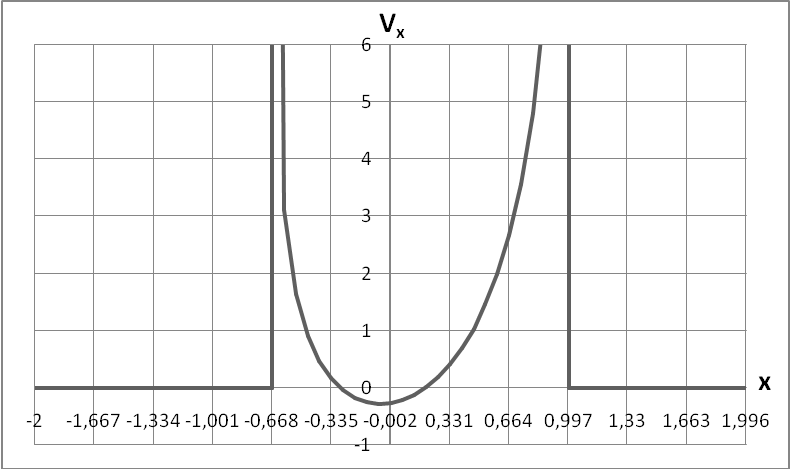

 є критичною, у ній імпульсна сила приймає нескінченні значення. Але ця точка відриву може виникнути лише тоді, коли кутова швидкість сягає дуже великих розмірів, порівняно з поступальною. В точках
є критичною, у ній імпульсна сила приймає нескінченні значення. Але ця точка відриву може виникнути лише тоді, коли кутова швидкість сягає дуже великих розмірів, порівняно з поступальною. В точках  та В точці
та В точці  маємо граничні випадки, коли відривне обтікання стає безвідривним, тобто точка відриву співпадає з кінцем пластини.
маємо граничні випадки, коли відривне обтікання стає безвідривним, тобто точка відриву співпадає з кінцем пластини.