
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Методы вычисления неопределённых интеграловI. Метод разложения (метод непосредственного интегрирования):основан на применении 3 и 4 правил интегрирования. Примеры:а) б) II. Метод замены переменной (метод подстановки):основан на формуле
Метод замены переменной применяют в двух случаях: 1) если интеграл похож на табличный, но аргументом выступает не Примеры:а) б) в) г) III. Метод интегрирования по частям:основан наформуле
где Большую часть интегралов, вычисляемых интегрированием по частям, можно разбить на три группы: 1) Интегралы вида Примеры:а)
б)
2) Интегралы вида Пример:
3) Интегралы вида Пример:
откуда
Определённый интеграл Определение 13.Пусть функция
называется интегральной суммой функции 
Если определенный интеграл существует, то функция называется интегрируемой на отрезке Для вычисления определённого интеграла применяется формула Ньютона-Лейбница:определённый интеграл от непрерывной на отрезке
Пример:
Основные свойства определённого интеграла 1) 2) 3) Каковы бы ни были числа 4) Постоянный множитель можно выносить за знак определённого интеграла:
5) Определённыйинтеграл от суммы (разности) двух функций равен сумме (разности) определённых интегралов этих функций:
6) Теорема о среднем: если функция 7) Если функция 8) Замена переменной в определённом интеграле: Примеры: 1) 2)
9) Интегрирование по частям в определённом интеграле: Пример:
Определённый интеграл применяется для вычисления площадей плоских фигур, длин дуг, объёмов тел. Приложения определённого интеграла |
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 206. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
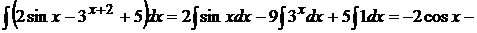
 ;
;
 .
. .
. , а линейное выражение, зависящее от
, а линейное выражение, зависящее от  ;
;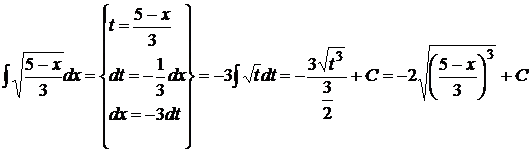 ;
; ;
; .
. ,
, и
и  – дифференцируемые функции от
– дифференцируемые функции от  свести к вычислению интеграла
свести к вычислению интеграла  , который может оказаться более простым для интегрирования.
, который может оказаться более простым для интегрирования. ,
,  ,
, 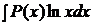 ,
,  ,
,  , где
, где  – многочлен, зависящий от
– многочлен, зависящий от  .
.
 ;
;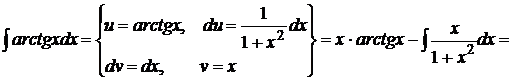
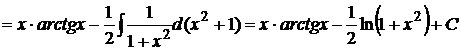 .
. ,
,  ,
, 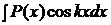 , где
, где  – число. Для их вычисления следует положить
– число. Для их вычисления следует положить  ,
,  ,
,  ,
,  соответственно.
соответственно.
 .
. ,
,  , где
, где  и
и  – числа, вычисляются двукратным применением метода интегрирования по частям.
– числа, вычисляются двукратным применением метода интегрирования по частям.
 Выписывая начало и конец равенства, получаем
Выписывая начало и конец равенства, получаем ,
, .
. определена и ограничена на отрезке
определена и ограничена на отрезке  и
и  – произвольное разбиение этого отрезка на
– произвольное разбиение этого отрезка на 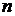 элементарных промежутков. Предположим, что на каждом отрезке
элементарных промежутков. Предположим, что на каждом отрезке  выбрана точка
выбрана точка  , тогда сумма
, тогда сумма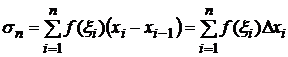
 , если он существует и конечен, называется определенным интегралом от функции
, если он существует и конечен, называется определенным интегралом от функции 
 равен приращению любой её первообразной на этом отрезке:
равен приращению любой её первообразной на этом отрезке: .
. .
.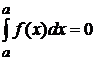 .
. .
. , имеет место равенство
, имеет место равенство 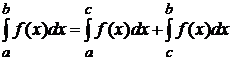 .
. , где
, где 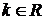 .
. .
. из этого отрезка, что
из этого отрезка, что  .
. , а если нечётная, то
, а если нечётная, то  .
. , где
, где  новые пределы интегрирования находятся из условий
новые пределы интегрирования находятся из условий 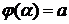 ,
,  .
. ;
;

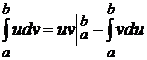 .
.
 .
.