
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Правила вычисления пределов последовательностей и функцийI. Подставить бесконечность вместо Например, Важно, что Если в результате подстановки получилось число или II. Если получилась неопределённость вида 1) разделить числитель и знаменатель дроби на старший член (на наивысшую степень или на наибольшее число в степени). Примеры:а)
Вывод:Если под знаком предела стоит дробь, в числителе и знаменателе которой многочлены одинаковых степеней, то предел равен отношению коэффициентов при старших степенях. б)
в) г)
д) е)
2) воспользоваться правилом Лопиталя: Пример: III. Если получилась неопределённость вида 1) сократить на выражение Примеры:а) б) 2) бесконечно малый множитель заменить на эквивалентный: при Пример: 3) воспользоваться правилом Лопиталя: Пример: 4) домножить и разделить на сопряжённое, если выражение, стоящее за знаком предела, имеет корни. Пример:
IV. Если получились неопределённости вида Примеры:а) б)
V. Если получилась неопределённость вида Примеры: а) б) в)
г) Тема 2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ Дифференциальное исчисление занимается изучением и приложениями производных. Рассмотрим основные моменты этого раздела сначала применительно к функциям одной переменной, а затем – к функциям нескольких переменных. 
Функции от одной переменной Определение 4.Производной функции
Производную функции Необходимым условием существования производной функции в заданной точке является непрерывность функции в этой точке (функция называется непрерывной в точке Операция нахождения производной функции называется дифференцированием. Функция, имеющая производную в точке Для вычисления производных используются таблица производных и правила дифференцирования.
Таблица производных 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14)
Правила дифференцирования 1) Постоянный множитель можно выносить за знак производной:
Пример: 2) Производная суммы (разности) двух функций, определённых на одном и том же промежутке, равна сумме (разности) производных этих функций:
Пример:
3) Производная произведения двух функций, определённых на одном и том же промежутке, вычисляется по формуле
Пример: 4) Если функции
Пример: 5) Если функция сложная, то есть
Пример: Если функция
где Определение 5. Главная, линейная относительно
Если
Определение 6.Производной второго порядка (второй производной) функции
если он существует. Аналогично производную от второй производной называют производной третьего порядка или третьей производной. В общем случае производной Производные второго, третьего и более высоких порядков вычисляются последовательным дифференцированием заданной функции. Примеры: 1) 2) С помощью пределов и производных производится исследование графиков функций. Изучение графика функции целесообразно производить по следующему плану.
|
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 190. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
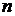 или предельное значение
или предельное значение  вместо
вместо  в выражение, стоящее за знаком предела.
в выражение, стоящее за знаком предела. ,
, .
.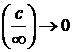 , где
, где  – любое число;
– любое число; 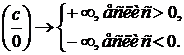
 , то это ответ. Очень часто после подстановки получаются неопределенности вида
, то это ответ. Очень часто после подстановки получаются неопределенности вида  ,
,  ,
,  ,
,  ,
,  .
.
 .
.
 ;
; ;
;
 ;
; ;
;
 .
.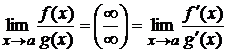 .
. .
. , которое стремится к нулю.
, которое стремится к нулю. ;
;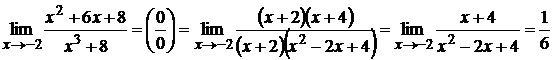 .
.
 ,
,  ,
,  ,
,  ,
,  ,
, 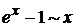 ,
, 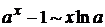 ,
,  ,
,  , где
, где 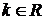 .
. .
.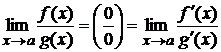 .
. .
.
 .
. ;
;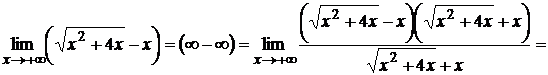

 ,
,  ,
,  .
. ;
;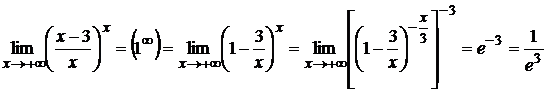 ;
;
 ;
; .
. в точке
в точке  называется предел отношения приращения
называется предел отношения приращения  функции в точке
функции в точке  при
при  в точке
в точке  :
: .
. в точке
в точке  ,
, 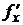 .
. , если она определена в окрестности данной точки и
, если она определена в окрестности данной точки и 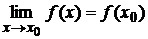 ). Обратное утверждение является неверным. Например, функция
). Обратное утверждение является неверным. Например, функция  непрерывна на промежутке
непрерывна на промежутке 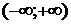 , но в точке
, но в точке  производной не имеет.
производной не имеет. , называется дифференцируемой на этом интервале.
, называется дифференцируемой на этом интервале. , где
, где  .
.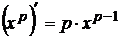 , где
, где  .
. .
.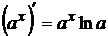 , где
, где  .
. .
. , где
, где  .
.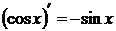 .
. .
.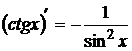 .
. .
. .
. .
. .
. , где
, где  .
. .
.
 .
. .
. .
. имеют в точке
имеют в точке 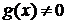 , то в этой точке существует производная их частного, которая вычисляется по формуле
, то в этой точке существует производная их частного, которая вычисляется по формуле .
. .
. , где
, где 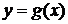 , то её производная может быть вычислена по правилу
, то её производная может быть вычислена по правилу .
. .
. можно записать в виде
можно записать в виде ,
,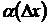 – бесконечно малая функция при
– бесконечно малая функция при  , то есть
, то есть 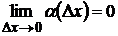 .
. . Следовательно,
. Следовательно,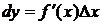 .
.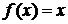 , то
, то  , поэтому формула для вычисления дифференциала будет следующей:
, поэтому формула для вычисления дифференциала будет следующей: .
.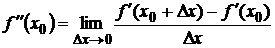 ,
, порядка:
порядка:  .
. ,
,  ,
,  ,
,  , … ,
, … ,  .
. ,
,  ,
,  ,
,  , … ,
, … ,  .
.