
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Функции нескольких переменныхОпределение 10. Пусть даны два непустых множества Например, Аналогично можно дать определение функции трёх переменных Графиком функции двух переменных в прямоугольной системе координат Частные производные В отличие от функций одной переменной, функции двух переменных имеют две производные первого порядка. Они называются частными производными. Частная производная функции Примеры.Найдём частные производные следующих функций: 1) 2)
Аналогично вычисляются частные производные функций трёх и более переменных. Например, для функции  Пусть функция
Частные производные второго порядка Пример. Найдём частные производные второго порядка от функции Сначала находим частные производные первого порядка: Затем находим частные производные второго порядка: Частные производные третьего порядка определяются как частные производные от частных производных второго порядка и так далее. Определение 11.Функция Теоремы, отражающие необходимые и достаточные условия экстремума, дают следующий алгоритм исследования функций от двух переменных на экстремум.
|
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 167. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и
и  , причём множество
, причём множество 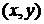 , а множество
, а множество  . Соответствие
. Соответствие 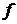 , которое каждому элементу
, которое каждому элементу  , определённой на множестве
, определённой на множестве  – функция от двух переменных. Область определения этой функции – множество всех пар чисел
– функция от двух переменных. Область определения этой функции – множество всех пар чисел  , для которых выполняется неравенство
, для которых выполняется неравенство  , то есть
, то есть  или первый и третий квадранты без оси
или первый и третий квадранты без оси  , а множество значений – промежуток
, а множество значений – промежуток  .
. , четырёх переменных
, четырёх переменных  и вообще
и вообще 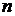 переменных
переменных  .
. является некоторая поверхность в пространстве.
является некоторая поверхность в пространстве. представляет собой обыкновенную производную функции одной переменной
представляет собой обыкновенную производную функции одной переменной  (обозначается
(обозначается  или
или  ), а частная производная функции двух переменных
), а частная производная функции двух переменных 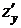 или
или  ). Поэтому частные производные вычисляются по формулам и правилам вычисления производных функции одной переменной.
). Поэтому частные производные вычисляются по формулам и правилам вычисления производных функции одной переменной. ;
;  ,
,  ;
; ,
, .
. ,
,  ,
,  ,
,  .
. и
и  . Если
. Если  ;
;  ;
; ;
;  .
. и
и  называются смешанными частными производными. Для непрерывных функций они равны.
называются смешанными частными производными. Для непрерывных функций они равны. .
. ,
,  .
. ,
,  ,
,  .
. , если для любой точки
, если для любой точки  , находящейся в некоторой окрестности точки
, находящейся в некоторой окрестности точки  (
(  ). Максимумы и минимумы функций называются экстремумами, а точка
). Максимумы и минимумы функций называются экстремумами, а точка