
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Алгоритм исследования функций двух переменных на экстремум1) Вычислить частные производные первого порядка: 2) Вычислить частные производные второго порядка 3) Найти значение дискриминанта а) Если б) Если в) Если Примеры. Найдём экстремумы функций: а) 1) Вычислим частные производные первого порядка: 2) Найдём частные производные второго порядка: 3) Вычисляем значение дискриминанта
б) 1) Частные производные первого порядка равны 2) Частные производные второго порядка равны 3) Дискриминант равен в) 1) Вычислим частные производные первого порядка: 2) Находим вторые частные производные: 3) 
г) 1) Вычисляем частные производные первого порядка:
2) Находим вторые частные производные: 3) Вычисляем значения всех дискриминантов и делаем выводы.
Тема 3. ИНТЕРАЛЬНОЕ ИСЧИСЛЕНИЕ Основная задача дифференциального исчисления заключается в нахождении производной от заданной функции. Интегральное исчисление решает обратную задачу: дана функция Определение 12.Функция Пример. Найдём первообразные для функции Вывод: Если функция Совокупность всех первообразных для функции
Для вычисления неопределённых интегралов используют таблицу основных интегралов, правила интегрирования и методы интегрирования.
Таблица неопредёленных интегралов 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16)
Правила интегрирования 1) 2) 3) Постоянный множитель можно выносить за знак неопределённого интеграла:
4) Интеграл суммы (разности) двух функций равен сумме (разности) интегралов этих функций:
|
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 183. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и
и  . Из системы
. Из системы  найти точки, подозрительные на экстремум (стационарные точки). Пусть
найти точки, подозрительные на экстремум (стационарные точки). Пусть  – стационарная точка функции
– стационарная точка функции  (таких точек может быть несколько).
(таких точек может быть несколько). ,
,  ,
, 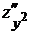 и их значения в стационарной точке:
и их значения в стационарной точке: 
 .
. .
. , то в точке
, то в точке  (или
(или 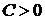 при
при  ), то в точке
), то в точке 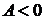 (или
(или 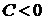 при
при  , то в точке
, то в точке  , то требуются дополнительные исследования.
, то требуются дополнительные исследования. .
. ,
,  . Из системы
. Из системы  находим точку
находим точку 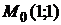 , подозрительную на экстремум.
, подозрительную на экстремум. ,
,  ,
,  . Значения вторых производных не зависят от
. Значения вторых производных не зависят от  и
и  , поэтому нет необходимости вычислять их величину в стационарной точке и
, поэтому нет необходимости вычислять их величину в стационарной точке и  ,
,  ,
,  .
. . Следовательно, в точке
. Следовательно, в точке  .
.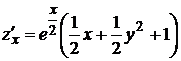 ,
,  . Точка
. Точка  – стационарная точка, так как её координаты являются решением системы
– стационарная точка, так как её координаты являются решением системы 
 ,
,  ,
,  . Вычислим их значения в стационарной точке:
. Вычислим их значения в стационарной точке:  ,
,  ,
,  .
. . Следовательно, в точке
. Следовательно, в точке 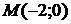 экстремум есть. Так как
экстремум есть. Так как  ,
, 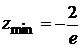 .
. .
. ,
,  . Находим стационарные точки, используя необходимые условия:
. Находим стационарные точки, используя необходимые условия:  ,
,  ,
,  ;
;  ,
,  . Следовательно,
. Следовательно,  ,
,  - стационарные точки.
- стационарные точки. ,
,  ,
,  и их значения в стационарных точках:
и их значения в стационарных точках: 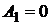 ,
,  ,
,  ;
;  ,
,  ,
,  .
. , поэтому в точке
, поэтому в точке  . Следовательно, в точке
. Следовательно, в точке  ,
, 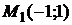 – точка максимума,
– точка максимума,  .
. .
. ,
,  . Из системы
. Из системы  находим стационарные точки:
находим стационарные точки:


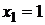 ,
, 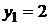 ;
;  ;
;  ,
,  ;
; 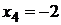 ,
,  . Следовательно,
. Следовательно,  ,
,  ,
, 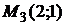 ,
,  – точки, подозрительные на экстремум.
– точки, подозрительные на экстремум. ,
,  ,
,  и их значения в стационарных точках:
и их значения в стационарных точках:  ,
,  ,
,  ;
; 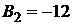 ,
,  ,
,  ,
,  ;
;  ,
,  ,
, 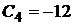 .
. . Следовательно, в точке
. Следовательно, в точке 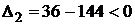 , поэтому в точке
, поэтому в точке  . Следовательно, в точке
. Следовательно, в точке  .
. , поэтому в точке
, поэтому в точке  – точка максимума,
– точка максимума,  .
. , требуется найти функцию
, требуется найти функцию  , такую, что
, такую, что  . Функция
. Функция  , если в каждой точке
, если в каждой точке  .
.  ,так как
,так как  . Функции
. Функции  и
и также являются первообразными для функции
также являются первообразными для функции  . Вообще, любая функция вида
. Вообще, любая функция вида  , где
, где  , является первообразной для функции
, является первообразной для функции  , где
, где  , также является первообразной для
, также является первообразной для 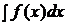 :
: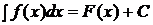 , где
, где  .
. , где
, где  ,
,  , где
, где  ,
,  ,
,  ,
,  , где
, где  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 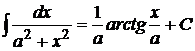 , где
, где  ,
,  , где
, где  , где
, где  ,
,  , где
, где  .
.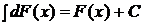 , где
, где  , где
, где 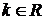 .
. .
.