
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Лексико-графический порядок.Пусть в списке букв конечного алфавита А порядок букв зафиксирован, т. е. всегда один и тот же, как, например, в русском и латинском алфавите. Тогда этот список определяет полное упорядочение букв, которое назовем отношением предшествования и обозначим “ На основе отношения предшествования букв, строится отношение предшествования слов, определяемое следующим образом: Пусть даны слова Тогда, 1) 2) Это отношение задает полное упорядочение множества всех конечных слов в алфавите А, которое является лексикографическим упорядочением слов. УПРАЖНЕНИЯ 1. Определите свойства отношений
Какие их этих отношений являются отношениями порядка, отношениями эквивалентности?
2. Определите свойства отношений
Задать эти отношения различными способами, если
Рис. 1 3. Определите свойства отношений

Задать эти отношения различными способами.
Рис. 2 4. Определите свойства отношений
Какие их этих отношений являются отношениями порядка, отношениями эквивалентности? 5. Определите свойства отношений
6. Определите свойства отношений
Сделать рисунок, задать 6 точек, на их примере построить матрицу бинарного отношения. Определить будут ли эти отношения отношениями эквивалентности. Если да, как разбивается плоскость на классы и каков индекс разбиения. Операции и алгебры N-арная операция на множестве М – это функция типа
где n – арность операции. Операция замкнута относительно множества М по определению, т. е. операция над элементами множества М, и результат тоже элемент М. Алгеброй называется множество, вместе с заданной на нем совокупностью операций
М – основное (несущее) множество (носитель алгебры) алгебры А. Тип алгебры – вектор арностей операций. Сигнатура – совокупность операций W. Множество
т. е. если значения Если
называется подалгеброй алгебры А (при этом Примеры: 1. Алгебра Обе операции бинарные, поэтому тип этой алгебры (2,2). Сигнатура Подалгеброй этой алгебры является, например, поле рациональных чисел. 2. Пусть
где с и d – остатки от деления на р чисел а + b и а × b соответственно. Пусть, например, р = 7, тогда
Часто обозначают: a + b = с (mod p) и a × b = d (mod p). Конечным полем характеристики р называется алгебра 3. Пусть задано множество U. Булеаном U называется множество всех подмножеств множества U (обозначается B(U)). Булева алгебра множеств над U или алгебра Кантора – алгебра Элементами основного множества булевой алгебры являются множества (подмножества U). Для любого Например, если |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 314. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ”:
”:  , если
, если  предшествует
предшествует  в списке букв).
в списке букв). и
и  .
. тогда и только тогда, когда
тогда и только тогда, когда , где
, где  - слова возможно непустые,
- слова возможно непустые,  - буквы);
- буквы); , где
, где 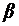 - непустое слово.
- непустое слово. и их вид, где М – множество натуральных чисел:
и их вид, где М – множество натуральных чисел: - ”быть меньше”;
- ”быть меньше”;  - ”быть больше или равно”;
- ”быть больше или равно”;  - ”иметь общий делитель, отличный от 1”;
- ”иметь общий делитель, отличный от 1”;  - ”быть делителем”;
- ”быть делителем”;  - ”иметь общий остаток от деления на 3”. Задать эти отношения различными способами, если
- ”иметь общий остаток от деления на 3”. Задать эти отношения различными способами, если  .
. - множество прямых на плоскости (см. рис 1):
- множество прямых на плоскости (см. рис 1):

 - ”быть непосредственно подчинённым”;
- ”быть непосредственно подчинённым”; - ”быть предком”;
- ”быть предком”; - ”быть потомком”.
- ”быть потомком”.
 .
.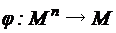 ,
, , т. е. система
, т. е. система .
. называется замкнутымотносительно n-арной операции
называется замкнутымотносительно n-арной операции  на М, если
на М, если ,
, принадлежат
принадлежат 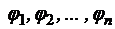 , алгебры М, то система
, алгебры М, то система
 – называется полем действительных чисел.
– называется полем действительных чисел.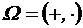 .
. . Определим на
. Определим на  операции:
операции:  – «сложение по модулю р»,
– «сложение по модулю р», 
 – «умножение по модулю р», следующим образом:
– «умножение по модулю р», следующим образом: и
и  ,
, и
и ,
,  ,
,  .
.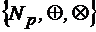 , если р – простое число.
, если р – простое число.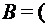 B(U),
B(U),  ). Ее тип (2,2,1), сигнатура
). Ее тип (2,2,1), сигнатура  (
( 
 B(
B(  ),
), 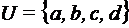 , то основное множество алгебры В содержит 16 элементов; алгебра
, то основное множество алгебры В содержит 16 элементов; алгебра 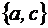 ),
),