
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Взаимно однозначные соответствия и мощность множествУтверждение (о взаимно однозначном соответствии равномощных множеств):Если между конечными множествами А и В существует взаимно однозначное соответствие, то Этот факт: 1) позволяет установить равенство мощностей двух множеств, не вычисляя мощностей этих множеств; 2) дает возможность вычислить мощность множества, установив его взаимно однозначное соответствие с множеством, мощность которого известна или легко вычисляется. Теорема (о числе подмножеств конечного множества) Если для конечного множества А ( Множества равномощны, если между их элементами можно установить взаимно однозначное соответствие. Счетные множества это множества равномощные N (т. е. между ними и N можно установить взаимно однозначное соответствие). Утверждение 1: Множество Утверждение 2: Любое бесконечное подмножество множества N – счетно. Утверждение 3: Множество Следствие: Множество Утверждение 4: Множество Утверждение 5: Объединение конечного числа счетных множеств Утверждение 6: Объединение счетного множества конечных множеств – счетно. Следствие: Множество всех слов конечного алфавита – счетно. Утверждение 7: Объединение счетного множества счетных множеств Несчетные бесконечные множества называются множествами мощности континуум. (Мощность несчетного бесконечного множества называется континуумом). Теорема (Кантора): Множество всех действительных чисел отрезка [0, 1] имеет мощность континуума. Следствие: Множество всех подмножеств несчетного множества континуально.  УПРАЖНЕНИЯ 1. Определите свойства соответствий между множествами 1) 2)
2. Соответствие задано рисунком. Определить свойства соответствия. Является ли оно функцией, отображением?
Рис 1. Рис.2. Рис.3. Для рис. 1 определить: 1) образ 2; 2) образ 4; 3) образ [2; 4]; 4) образ (2; 4]; 5) прообраз 2; 6) прообраз 4; 7) прообраз [2;4]; 8) прообраз (0;4). Для рис. 2 определить: 1) образ 2; 2) образ 4; 3) образ [2; 4]; 4) образ (4; 6]; 5) прообраз 0; 6) прообраз 4; 7) прообраз [0;4]; 8) прообраз (0;4). Для рис. 3 определить: 1) образ 2; 2) образ 4; 3) образ [2; 4]; 4) образ (0; 4]; 5) прообраз 2; 6) прообраз 4; 7) прообраз [2;4]; 8) прообраз (2;4).
3. Определите свойства соответствий между множествами 1) 2) 4. Определите, какие из следующих подмножеств 1)
2)
5. Пусть
6. Дано множество
или, как обычно принято записывать преобразования конечных множеств:
Найти композиции преобразований:
7. Найти композиции преобразований: 1) 2) 3)
8. Пусть тип функции 1) 2) 3) 4) 5) б) A= 9. Определить область определения и область значений композиций 1) 2) 3) 10. Найти композиции преобразований: 1) 2) 3) 11. Найти композиции 1) 2) 3) 4) Отношения Подмножество Одноместное отношение – это просто подмножество М. Такие отношения называют признаками: элемент а – обладает признаком R, если Свойства одноместных отношений это свойства подмножеств М, поэтому для случая n = 1 термин “отношение” употребляется редко. Примером трехместного (тернарного) отношения является множество троек нападающих в хоккейной команде. Любой из нападающих находится в этом отношении со всеми теми игроками, с которыми он играет в одной тройке (один нападающий может, вообще говоря, участвовать более, чем в одной тройке). При n = 2 – отношения называются двуместными или “бинарными”. Если a, b находятся в отношении R, это записывается aRb. Пусть дано отношение R на М. Для любого подмножества
|
||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 332. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
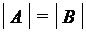 .
.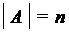 ), то число всех подмножеств множества А равно
), то число всех подмножеств множества А равно 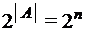 .
.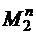 – счетно.
– счетно.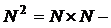 – счетно.
– счетно.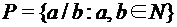 – положительных рациональных чисел – счетно.
– положительных рациональных чисел – счетно.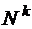 , где
, где 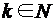 , - счетно.
, - счетно.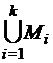 – счетно.
– счетно.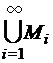 – счетно.
– счетно.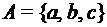 и
и 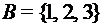 . Какие из них являются функциями типа
. Какие из них являются функциями типа 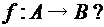
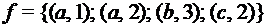 ; 3)
; 3) 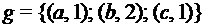 ;
;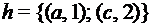 ; 4)
; 4) 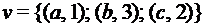 .
.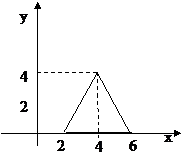


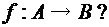
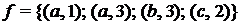 ; 3)
; 3) 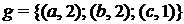 ;
;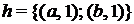 ; 4)
; 4) 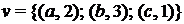 .
.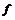 множества
множества 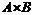 являются функциями
являются функциями 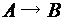 . Объясните свой ответ.
. Объясните свой ответ.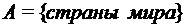 ,
, 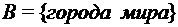 ,
,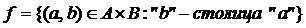
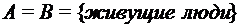 ,
,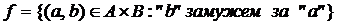
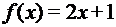 ,
, 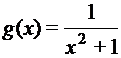 – функции
– функции 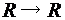 . Найдите:
. Найдите: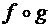 ;
;
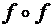 ;
;
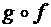 ;
;
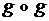 .
.
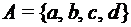 и два преобразования этого множества (т.е. функции типа
и два преобразования этого множества (т.е. функции типа 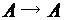 ):
):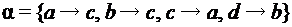 и
и 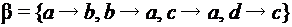
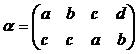 и
и 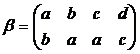 .
.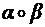 и
и 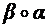 .
.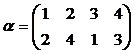 и
и 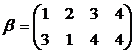 ;
;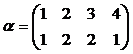 и
и 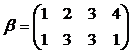 ;
;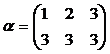 и
и 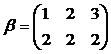 .
. 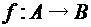 . Для различных А, В и f определить область определения и область значения. Будут ли у этих функций обратные? Если да, то будут ли они отображениями. Сделайте вывод о том, какими свойствами должна в этом случае обладать функция.
. Для различных А, В и f определить область определения и область значения. Будут ли у этих функций обратные? Если да, то будут ли они отображениями. Сделайте вывод о том, какими свойствами должна в этом случае обладать функция.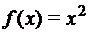 , если а) А=R; В=R; б) A=N; В=N.
, если а) А=R; В=R; б) A=N; В=N.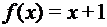 , если а) А=R+; В=R; б) A=N0; В=N.
, если а) А=R+; В=R; б) A=N0; В=N.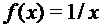 , если а) А=R; В=R; б) A=R+; В=R.
, если а) А=R; В=R; б) A=R+; В=R.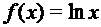 , если а) А=R; В=R; б) A=R+; В=R+.
, если а) А=R; В=R; б) A=R+; В=R+.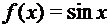 , если а) А=R; В=R;
, если а) А=R; В=R;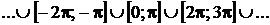 ; В=[0; 1].
; В=[0; 1].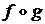 и
и 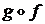 .
. 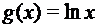 ; г)
; г) 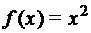 ;
; 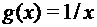 ;
;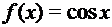 ;
; 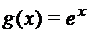 ; д)
; д) 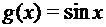 ;
;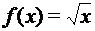 ;
; 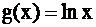 .
.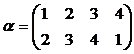 и
и 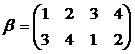 ;
;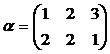 и
и 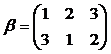 ;
; 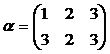 и
и 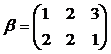 .
.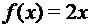 и
и 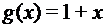 - функции типа
- функции типа 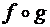 =
= 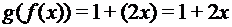 ;
;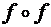 =
= 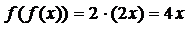 ;
;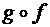 =
= 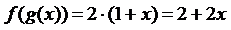 ;
;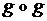 =
=  .
. называется n - местным отношением на множестве М. Говорят, что
называется n - местным отношением на множестве М. Говорят, что 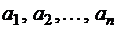 находится в отношении R, если
находится в отношении R, если 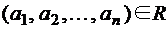 .
.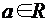 и
и 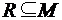 .
.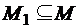 естественно определяется отношение
естественно определяется отношение 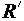 , называемое сужением R на
, называемое сужением R на 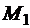 , которое получается из R удалением всех пар, содержащих элементы, не принадлежащие
, которое получается из R удалением всех пар, содержащих элементы, не принадлежащие 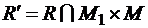 . Строго говоря, R и
. Строго говоря, R и