
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Классическое определение вероятностиЕсли множество элементарных событий Условной вероятностью Условная вероятность
События А и В – называются независимыми, если при происхождении одного из них не изменяется вероятность происхождения другого. Для независимых событий выполняется равенство Очевидно, что для независимых событий справедливо:
События
Если это соотношение выполняется при k = 2, то события Теорема сложения. Вероятность суммы двух событий равна сумме вероятностей этих событий без вероятности их совместного появления: p(А+В) = p(А) + p(В) – p(АВ). Если события А и В несовместны, то p(А+В) = p(А) + p(В). Теорема умножения. Вероятность совместного наступления двух событий равна вероятности одного из них, умноженной на условную вероятность другого при условии, что первое событие наступило:
Если события А и В независимы, то Пример 1. Брошены три монеты. Найти вероятность того, что выпадут две “решки”. Пространство элементарных событий данного стохастического эксперимента:  Пример 2. В студенческой группе из 15 девушек и 10 юношей по жребию разыгрывается билет в театр. Какова вероятность, что билет достанется девушке? Событию A = «билет достался девушке» благоприятствует 15 элементарных событий ( Следовательно, Пример 3. Студент пришел на экзамен, зная лишь 20 из 25 вопросов программы. Экзаменатор задал студенту 3 вопроса. Найти вероятность того, что студент знает все эти вопросы. Рассмотрим событие А = «студент знает ответы на все три заданных вопроса». Оно состоит из события Таким образом, по теореме умножения вероятностей
(Или по классическому определению вероятности: Пример 4. Для сигнализации о возгорании установлены два независимо работающих датчика. Вероятности того, что при возгорании датчик сработает для первого и второго датчиков соответственно равны 0,9 и 0,95. Найти вероятность того, что при пожаре сработает: а) хотя бы один датчик; б) только один датчик. Обозначим: Вероятность того, что при возгорании сработает хотя бы один датчик (событие А) можно вычислить по теореме сложения вероятностей: Вероятность того, что при возгорании сработает только один датчик (событие В) равна УПРАЖНЕНИЯ 1. Определить, обладает ли следующая группа событий свойствами группы случаев: 1) Испытание состоит в бросании 2х монет. А 2) Испытание состоит в 2х выстрелах по мишени. А 3) Испытание состоит в бросании игральной кости. А 2. В классе 15 учеников. Из них 8 юношей. Наугад выбирают одного человека. Какова вероятность того, что это девушка? 3. Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 20. Найти вероятность того, что номер первого наудачу извлеченного жетона не содержит цифру 5. 4. В урне 12 шаров. Из них 3 белых, 2 синих, остальные черные. Наугад выбирают один шар. Какова вероятность того, что он синий? 5. Слово МОЛНИЯ разрезали на буквы, берут наугад четыре буквы и выкладывают в ряд. Какова вероятность того, что получится слово МИЛЯ? 6. На пяти одинаковых на ощупь карточках написаны буквы: на двух карточках – буква Л и на трех карточках – буква И. Эти карточки выкладываются наугад в один ряд. Какова вероятность того, что выложится слово ЛИЛИИ? 7. Замок открывается только при наборе шифра – трехзначное число без повторения цифр. Какова вероятность того, что замок откроется, если шифр набран случайно? 8. Семь различных книг расставляются на одной полке случайным образом. Какова вероятность того, что две определенные книги окажутся поставленными рядом? 9. В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов: 1) все отличники; 2) только пять отличников. 10. В коробке 3 чёрных и 2 белых (одинаковых на ощупь) кубиков. Наудачу извлекаются два кубика. Найти вероятность того, что среди них окажутся: 1) один чёрный кубик; 2) два чёрных кубика; 3) хотя бы один чёрный кубик. 11. Из 30 экзаменационных билетов студент подготовил только 25. Если он отказывается отвечать по первому взятому билету (которого он не знает), то ему разрешается взять второй. Определить вероятность того, что второй билет окажется счастливым. 12. Студент пришел на зачет, зная из 30 вопросов только 24. Какова вероятность сдать зачет, если он вытаскивает вопрос 1) первым; 2) вторым; 3) третьим? 13. Достаточным условием сдачи коллоквиума является ответ на один из двух вопросов, предлагаемых студенту преподавателем. Студент не знает ответов на 8 вопросов из тех 40, которые могут быть ему заданы. Какова вероятность того, что студент сдаст коллоквиум? 14. Слово ПАПАХА составлено из букв разрезной азбуки. Карточки с буквами тщательно перемешиваются. Четыре карточки извлекаются по очереди и раскладываются в ряд. Какова вероятность получить таким путем слово “ПАПА”? 15. В ящике 10 красных носков и 6 синих. Вынимаются наудачу два носка. Какова вероятность того, что носки будут одного цвета? 16. В одном ящике 5 белых и 10 красных шаров, в другом ящике 10 белых и 5 красных шаров. Найти вероятность того, что хотя бы из одного ящика будет вынут белый шар, если из каждого ящика вынуто по одному шару. 17. В студии телевидения 3 телевизионных камеры. Для каждой камеры вероятность того, что она включена в данный момент, равна 0,6. Найти вероятность того, что в данный момент включена хотя бы одна камера. 18. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0.9. Найти вероятность того, что из двух проверенных изделий: 1) только одно стандартное; 2) хотя бы одно стандартное. 19. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7; а для второго – 0,8. Найти вероятность того, что при одном залпе в мишень попадет: 1) только один из стрелков; 2) хотя бы один из стрелков. 20. Вероятность того, что до окончания работы выйдет из строя первый, второй и третий компьютер соответственно равны р1 = 0,1; р2 = 0,2; р3 = 0,1. Какова вероятность того, что до окончания работы выйдет из строя: 1) только один компьютер; 2) только два компьютера; 3) ни один компьютер; 4) хотя бы один компьютер задача. 21. Вероятность поскользнуться и упасть в гололед для взрослого – 0,3; для ребенка – 0,5. Какова вероятность того, что: 1) упадут оба; 2) упадет ровно один из них; 3) не упадет ни один.
Соответствия и функции Соответствием множеств А и В называется подмножество G такое, что Соответствие G называетсявсюду (полностью) определенным– если пр1 G = А (в противном случае – частично определенное соответствие). Соответствие G называетсясюрьективным, если пр2 G = B. Образэлемента aв множестве B при соответствии G – это множество всех элементов Образом множестваСÎ пр1 G называется объединение образов всех элементов С. Прообразом множестваD Î пр2 G называется объединение прообразов всех элементов D. Соответствие G называетсяфункциональным (однозначным)соответствием, если образом любого элемента из пр1 G является единственный элемент из пр2 G. Соответствие G называетсяинъективнымсоответствием, если прообразом любого элемента из пр2 G является единственный элемент из пр1 G. Соответствие F является функцией типа Соответствие G является отображением множества А в множество В, если оно функционально и полностью определено. Соответствие G является взаимно однозначным, если оно: 1) всюду определено; 2) сюрьективно; 3) функционально; 4) инъективно. Преобразованием множестваАназывается отображение типа Функция типа Соответствие Если соответствие, обратное к функции Пусть дана функция Утверждение:Для функции Пусть даны функции Функция Для многоместных функций Для множества многоместных функций типа Функция, полученная из функций |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 386. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
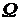 состоит из n равновозможных элементарных событий, то вероятность р(А) события А равна числу m элементарных событий, входящих в А, деленному на число всех элементарных событий, т. е.
состоит из n равновозможных элементарных событий, то вероятность р(А) события А равна числу m элементарных событий, входящих в А, деленному на число всех элементарных событий, т. е.  .
.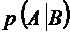 называют вероятность события А, вычисленную в предположении, что событие В уже наступило.
называют вероятность события А, вычисленную в предположении, что событие В уже наступило.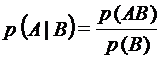 , где
, где  .
. .
. .
.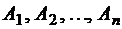 называются независимыми в совокупности, если для любых k из них
называются независимыми в совокупности, если для любых k из них  выполняется соотношение:
выполняется соотношение: .
. называются попарно независимыми.
называются попарно независимыми. .
. .
. ). Число благоприятных элементарных исходов для события A = «выпали две “решки”» = {ОРР, РОР, РРО} равно 3 (
). Число благоприятных элементарных исходов для события A = «выпали две “решки”» = {ОРР, РОР, РРО} равно 3 (  ). Следовательно,
). Следовательно,  .
. ) из 25 равновозможных (
) из 25 равновозможных (  ).
). .
. – «студент знает ответ на 1-ый вопрос» Исобытия
– «студент знает ответ на 1-ый вопрос» Исобытия  – «студент знает ответ на 2-ой вопрос» И события
– «студент знает ответ на 2-ой вопрос» И события  – «студент знает ответ на 3-ий вопрос».
– «студент знает ответ на 3-ий вопрос».  . Если студент ответил на первый вопрос, то всего осталось 19 вопросов, которые он знает из 24 оставшихся, следовательно, вероятность второго события, при условии, что первое произошло равна
. Если студент ответил на первый вопрос, то всего осталось 19 вопросов, которые он знает из 24 оставшихся, следовательно, вероятность второго события, при условии, что первое произошло равна 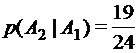 . Аналогично
. Аналогично  .
. .
. , где число благоприятных событий
, где число благоприятных событий 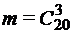 число – сочетаний из 20 знакомых вопросов по три; число всевозможных событий
число – сочетаний из 20 знакомых вопросов по три; число всевозможных событий  – число сочетаний из всех 25 вопросов по три.)
– число сочетаний из всех 25 вопросов по три.) – вероятность срабатывания 1-го датчика, тогда вероятность его несрабатывания равна
– вероятность срабатывания 1-го датчика, тогда вероятность его несрабатывания равна  ;
;  – вероятность срабатывания 2-го датчика, тогда вероятность его несрабатывания равна
– вероятность срабатывания 2-го датчика, тогда вероятность его несрабатывания равна 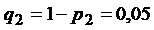 .
. или через противоположное событие (оба датчика не сработали):
или через противоположное событие (оба датчика не сработали): 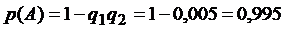 .
. .
. - выпал хотя бы один «герб»; А
- выпал хотя бы один «герб»; А 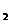 - выпала хотя бы одна «решка».
- выпала хотя бы одна «решка». - ровно два попадания.
- ровно два попадания. . Если
. Если  , то говорят, что “b соответствует a при соответствии G”. Область определения соответствия G – множество пр1 G Í A. Область значений соответствия G – множество пр2G Í B.
, то говорят, что “b соответствует a при соответствии G”. Область определения соответствия G – множество пр1 G Í A. Область значений соответствия G – множество пр2G Í B.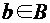 , которые соответствуют
, которые соответствуют  . Прообразэлемента b в множестве А при соответствии G – это множество всех
. Прообразэлемента b в множестве А при соответствии G – это множество всех  , если оно функционально (однозначно) (
, если оно функционально (однозначно) (  ).
).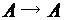 .
.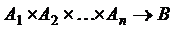 называется n-местной функцией (
называется n-местной функцией (  ).
).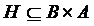 называется обратным к
называется обратным к 
 .
.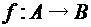 является функциональным, то оно называется функцией, обратной к f (
является функциональным, то оно называется функцией, обратной к f (  ).
). .
. называется композицией функций f и g, если
называется композицией функций f и g, если  (обозначение
(обозначение 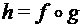 ). Часто говорят, что h получена подстановкой f в g.
). Часто говорят, что h получена подстановкой f в g. и
и  возможны различные варианты подстановки f в g, задающие функции различных типов. Например, при
возможны различные варианты подстановки f в g, задающие функции различных типов. Например, при  и
и  функция
функция  имеет 6 аргументов и тип
имеет 6 аргументов и тип 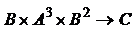 .
.
 возможны любые подстановки функций друг в друга, а также любые переименования аргументов. Например, переименование
возможны любые подстановки функций друг в друга, а также любые переименования аргументов. Например, переименование  в
в  из функции
из функции  четырёх аргументов порождает функцию трёх аргументов:
четырёх аргументов порождает функцию трёх аргументов:  .
. некоторой подстановкой их друг в друга и переименованием аргументов, называется суперпозицией функций
некоторой подстановкой их друг в друга и переименованием аргументов, называется суперпозицией функций