
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Введение в дискретную теорию вероятностейСтохастический эксперимент - это эксперимент, результат которого заранее (до его проведения) предугадать нельзя. Каждый неразложимый исход опыта (эксперимента) называется элементарным событиеми обозначается Случайным событием или просто событиемназывается любое подмножество пространства элементарных событий Свойства элементарных событий: - элементарные события являются взаимно исключающими друг друга; - в результате опыта обязательно происходит одно из элементарных событий; - каково бы ни было случайное событие А, по наступившему элементарному событию можно сказать о том, произошло или не произошло событие А. Пусть Таким образом, событие А состоит в том, что произошло одно из элементарных событий, входящих в указанное множество А. То есть мы отождествляем событие А и соответствующее ему множество А элементарных событий. Событие, состоящее из всех возможных элементарных событий  Невозможным называется событие, не наступающее ни при каком элементарном событии. Ему соответствует пустое множество элементарных событий: Соотношения между событиями: 1. Если каждое появление события А сопровождается появлением события В, то говорят, что А влечет В, или А является частным случаем В, или В является следствием события А, или А благоприятствует В ( 2. События А и В называются равносильными (равными, эквивалентными) ( 3. Суммой (объединением) событий А и В ( Очевидно, что: 4. Произведением (пересечением) двух событий А иВ (АВ или Очевидно, что: 5. Два события называются несовместными, если их одновременное появление в опыте невозможно. Следовательно, если А и В несовместны, то АВ = Элементарные события попарно несовместны: 6. Событием, противоположным событию А ( Очевидно, что: 7. Разностью событий А и В ( Очевидно, что: 8. События Свойства операций над событиями: 1. 3. 5. A(BC) = (AB)C, 6. A + (B + C) = (A + B) + C ; 6. A(B + C) = AB + AC ; 7. Рассмотрим пространство элементарных событий Система событий F называется алгеброй событий, если выполняются условия: 1) 2) если 3) если А и В Отсюда следует, что применяя любые из введенных выше операций к произвольной системе событий из F, получим событие, так же принадлежащее F. Таким образом, алгеброй событий называется класс событий, замкнутый относительно операций объединения, пересечения и дополнения. Вероятность события численно характеризует степень объективной возможности этого события. Пусть
Аксиомы Колмогорова Если каждому событию 1) 3) если А и В несовместны тогда число р(А) называется вероятностьюслучайного события А. Свойства вероятности 1) 2) Если события A и В - несовместны, то р(А+В) = р(А) + р(В); 3) Пространство элементарных событий |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 283. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
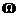 . Множество всех элементарных событий, относящихся к одному и тому же эксперименту, называется пространством элементарных событий и обозначается
. Множество всех элементарных событий, относящихся к одному и тому же эксперименту, называется пространством элементарных событий и обозначается 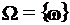 .
.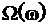 . События обозначают прописными буквами латинского алфавита A, B, C, . . .
. События обозначают прописными буквами латинского алфавита A, B, C, . . .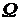 - пространство элементарных событий рассматриваемого опыта. Для каждого возможного в этом опыте события А выделим совокупность всех элементарных событий, наступление которых необходимо влечет наступление А. Говорят, что эти элементарные события благоприятствуют событию А. (Множество этих элементарных событий обозначают тем же символом А, что и соответствующее событие).
- пространство элементарных событий рассматриваемого опыта. Для каждого возможного в этом опыте события А выделим совокупность всех элементарных событий, наступление которых необходимо влечет наступление А. Говорят, что эти элементарные события благоприятствуют событию А. (Множество этих элементарных событий обозначают тем же символом А, что и соответствующее событие).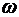 , называется достоверным и обозначается
, называется достоверным и обозначается 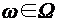 ).
).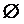 .
.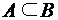 ). Если
). Если 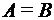 ), если они состоят из одних и тех же элементарных событий, т.е. всегда происходят или не происходят одновременно.
), если они состоят из одних и тех же элементарных событий, т.е. всегда происходят или не происходят одновременно.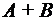 или
или 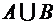 ) называется событие, которое состоит из элементарных событий, входящих хотя бы в одно из событий А и В, т. е. событие, происходящее тогда и только тогда, когда происходит хотя бы одно из событий А и В (или А или В)
) называется событие, которое состоит из элементарных событий, входящих хотя бы в одно из событий А и В, т. е. событие, происходящее тогда и только тогда, когда происходит хотя бы одно из событий А и В (или А или В)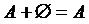 ;
; 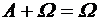 , А + А = А.
, А + А = А.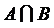 ) называется событие, которое состоит из элементарных событий, входящих и в событие А, и в событие В одновременно, т. е. событие, происходящее только тогда, когда происходит и событие А, и событие В.
) называется событие, которое состоит из элементарных событий, входящих и в событие А, и в событие В одновременно, т. е. событие, происходящее только тогда, когда происходит и событие А, и событие В.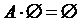 ;
; 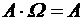 ;
; 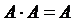 .
.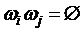 при
при 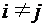 .
.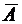 ) называется событие, которое состоит из всех элементарных событий, не входящих в А. Противоположное событие происходит тогда и только тогда, когда А не происходит.
) называется событие, которое состоит из всех элементарных событий, не входящих в А. Противоположное событие происходит тогда и только тогда, когда А не происходит.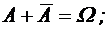
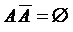 ;
; 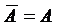 .
.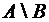 или
или 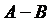 ) называется событие, происходящее тогда и только тогда, когда происходит событие А и не происходит событие В.
) называется событие, происходящее тогда и только тогда, когда происходит событие А и не происходит событие В. 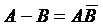 ;
; 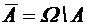 .
.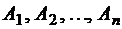 образуют полную группу событий, если
образуют полную группу событий, если 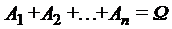 .
.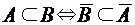 ; 2.
; 2. 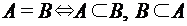 ;
;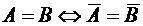 ; 4. A + B = B + A, AB = BA ;
; 4. A + B = B + A, AB = BA ;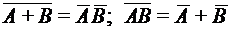 .
.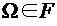 ;
;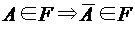 ;
;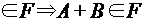 и
и 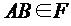 .
.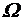 выделена система событий F, являющаяся алгеброй событий.
выделена система событий F, являющаяся алгеброй событий.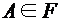 поставлено в соответствие число р(А) и верны свойства:
поставлено в соответствие число р(А) и верны свойства: ; 2)
; 2) 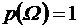 ;
;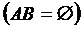 , то р(А+В) = р(А) + р(В),
, то р(А+В) = р(А) + р(В),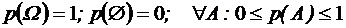 ;
;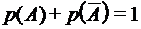 .
.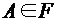 , называется вероятностным пространством и обозначается (
, называется вероятностным пространством и обозначается (