Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Мощности в цепи синусоидального напряжения.
1) Мгновенная мощность:
=
2) Активная мощность (средняя за период):
из ∆-ка напряжений (послед.): из ∆-ка токов (
3) Реактивная мощность:
из ∆-ка напряжений (послед.): из ∆-ка токов (
4) Полная мощность:
Желательно, чтобы
Символический метод расчета электрических цепей. (Метод комплексных амплитуд) Используется для расчета сложных электрических цепей алгебраически (~ - тильда).
В символическом методе синусоидальная функция заменяется ее символом комплексной функции.
⊜ Комплексную функцию можно отобразить на комплексной плоскости в виде радиус-вектора:
Умножение на При выполнении линейных операций над гармоническими функциями в символической форме ( +, приписывается к результату.
4.7.1. Дифференцирование и интегрирование гармонических функций в символической форме. 
1)
2)
4.7.2. Последовательное соединение R, L, C – элементов. Расчет символическим методом.
Дано: Определить:
По 2зК: Заменим 1) 2) Тогда 3) 4) 5)
(2)
Решение задачи:
Построим векторную диаграмму в комплексной плоскости:
1) 2) 3)
Умножение вектора на 4) ⊜
4.7.3. Параллельное соединение R, L, C.
Дано: Определить:
Решение: 1) по 1зК: 2) Заменяем мгновенные значения токов и напряжений соответствующими комплексами
Тогда,
где
=
= 𝒴 - комплексная проводимость цепи.
где 𝜑 – аргумент , |𝒴| - модуль,
По закону Ома находим
4.7.4. Эквивалентные участки цепи.
=
1) 𝒴→Z ;
где 2) Z → 𝒴 ;
4.7.5. Законы Ома и Кирхгофа в символической форме. 1) 1з.Ома (уже выводился):
2) Законы Кирхгофа 1зК: 2зК:
Правило знаков такое же, как в цепи постоянного тока.
Методы расчета цепей синусоидального тока в символической форме. Все методы расчета цепей постоянного тока (МКТ, МР и др.) применимы для цепей синусоидального тока в символической форме. Метод узловых потенциалов, например:
4.7.7. Мощности в символической форме.
Баланс мощностей в цепях синусоидального тока.
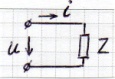
В равенствах (1), (2), (3) выражается баланс мощности в цепях синусоидального тока. Равенства (2), (3) перепишем в развернутом виде: Для активной мощности: Для реактивной мощности:
Глава 5. Частотные характеристики линейных электрических цепей. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 537. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |



 =
=  =
= [BA] – вольт-ампер
[BA] – вольт-ампер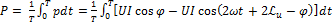 =
=  [Bт]
[Bт]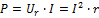
 ):
): 
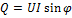 [BAp]
[BAp]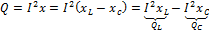


 [BA]
[BA] ∆-к мощностей:
∆-к мощностей:
 ;
; 
 - коэффициент мощности.
- коэффициент мощности. , так как при этом уменьшаются потери электроэнергии в проводах.
, так как при этом уменьшаются потери электроэнергии в проводах. - комплекс мгновенного значения напряжения.
- комплекс мгновенного значения напряжения.

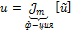

 ⊜ , где
⊜ , где - комплексная амплитуда (комплексное число).
- комплексная амплитуда (комплексное число).


 – оператор поворота.
– оператор поворота. против часовой стрелки.
против часовой стрелки. , умножение на const, дифференцирование и интегрирование)
, умножение на const, дифференцирование и интегрирование)  , где
, где 



 ;
;  , L, C .
, L, C . 
 ⇒ 𝜑 - ?
⇒ 𝜑 - ? (1)
(1) и
и  соответствующими комплексами:
соответствующими комплексами: , где
, где 




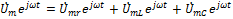 =
= 

 -
- 
 – комплексное сопротивление цепи.
– комплексное сопротивление цепи. ;
; 
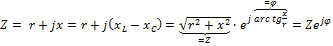
 =
= 



 ∆-к напряжения
∆-к напряжения 




 означает его поворот на
означает его поворот на  против часовой стрелки.
против часовой стрелки.
 ⊜
⊜


 ;
;  , L, C .
, L, C . 
 ⇒ 𝜑 - ?
⇒ 𝜑 - ? (1)
(1)  ;
;  , где
, где  ,
, 
 ,
, и
и 

 = (2)
= (2)



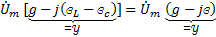 (3) -
(3) - 
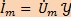 или
или  - закон Ома
- закон Ома ,
,  , где
, где  - полная проводимость
- полная проводимость
 :
: =
= 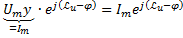







 =
=  =
=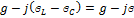 =
= 
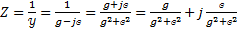 =
= 
 ;
; 
 аналогично
аналогично , где
, где  , где
, где  - при параллельном соединении
- при параллельном соединении - при включенном ЭДС
- при включенном ЭДС , где
, где 
 , где
, где 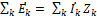
 - токи для действительных значений
- токи для действительных значений

 ,
, 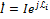




 ;
;  ;
; 

 (1)
(1)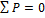
 (2)
(2)
 (3)
(3)