
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Элементарные двухполюсники в цепи синусоидального напряжения.4.4.1. Активное сопротивление в цепи синусоидального напряжения. Сопротивление в цепи переменного тока называется активным (r). Оно отличается от сопротивления R в цепи постоянного тока, называющееся омическим. Это отличие связано с поверхностным эффектом (явлением вытеснения переменного тока от центра проводника к его поверхности).
r = K ∙ R , где К – коэффициент (К > 1) K = F (
Поверхностный эффект считается при больших токах (сотни ампер), а так же на частотах больше 100 кГц. Будем считать, что r = R (в звукотехнике).
u =
Следствия: 1) 2) 𝜑 = 3)
Временные диаграммы:
Мгновенная мощность:
=
Активная мощность или средняя за период:
Пусть
4.4.2. Индуктивность цепи синусоидального напряжения.
A = 0 , т.к. в установившимся режиме синусоидальный ток не содержит постоянную составляющую ⊜
Выводы: 1)
2)
3)
4)
- ток ленивый (отстает на
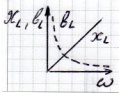
Частотные характеристики  сопротивления и проводимости.
=
Четверть периода Другую четверть периода
Подставляем синусоидальную функцию:
Примечание: реальная катушка индуктивности, кроме индуктивности L, обладает активным сопротивлением провода:
Чем выше
4.4.3. Емкость цепи синусоидального напряжения.
= Сравнение двух последних равенств: 1)
2)
3) 4)
=
Полагая, что
Реальный конденсатор, кроме емкости, обладает активной проводимостью, которая учитывает потерю энергии в диэлектрике, разделяющем пластины конденсатора.
Чем выше 𝛿 - угол диэлектрических потерь. Он зависит от сорта диэлектрика и частоты. В лучшем случае он равен нескольким секундам, в худшем – нескольким градусам.
4.4.4. Последовательное соединение R, L, C – элементов.
Дано: r, L, C , Определить:
Решение: Законы Кирхгофа применены к мгновенным значениям ⇒ ⇒ по 2зК: = Заменим сложение трех синусоидальных функций в тригонометрической форме сложением, изображающим их векторa.
Первый вектор произвольно:
1) (аналогично для действующих значений)
2) Могут быть 3 случая: 1 сл.) при
2 сл.) при
3 сл.) при
Из ∆-ка напряжений :
Если все стороны ∆-ка разделить на
←∆-к тока:
4.4.5. Параллельное соединениеR, L, C в цепи.
Дано: Определить:
Решение: По 1зК:
§4.5. Дуальные электрические цепи. Под условием дуальности понимается такое соответствие электрических цепей, при котором закон изменения контурных токов в одной цепи подобен закону изменения узловых напряжений в другой цепи.
Для таких элементов зависимости между напряжениями и токами имеют вид: (1) Следует иметь в виду, что входящие в системы (1) и (2) напряжения и токи, имеющие одинаковые буквенные обозначения, не равны друг другу. Из сравнения уравнений (1) и (2) видно, что условию дуальности удовлетворяют следующие элементы: 1) сопротивление и проводимость; 2) индуктивность и емкость; 3) источник ЭДС и источник тока. Элементы цепи, удовлетворяющие условию дуальности, называются аналогами или дуальными элементами. При последовательном соединении элементов цепи суммируются напряжения, при параллельном соединении элементов цепи – токи. Поэтому последовательному соединению элементов соответствует параллельное соединение их аналогов, а параллельному соединению – последовательное соединение их аналогов. Например:
Уравнение напряжений для исходной цепи (левый рисунок) подобно уравнению токов для второй цепи: Если ЭДС и ток источников подчинены одному и тому же закону и имеют одинаковую начальную фазу, то законы изменения контурного тока левой части примера и узлового напряжения левой части совпадают при соблюдении пропорции: В случае сложной электрической цепи каждой ее области, ограниченной независимым контуром, с учетом также области, внешней по отношению ко всей цепи, соответствует узел дуальной цепи. Следовательно, число областей заданной цепи равно числу узлов дуальной цепи. При построении дуальной цепи по отношению к заданной планарной цепи удобно пользоваться графическим приемом, простая форма которого была показана на рисунке. В каждой области, ограниченной независимым контуром заданной цепи, наносится точка, рассматриваемая в качестве будущего узла дуальной цепи. Узлы, соответствующие каждой паре смежных областей, соединяются параллельными ветвями, число которых равно числу элементов, последовательно включенных в цепь, граничащую с указанными областями. Элементами параллельных ветвей являются аналоги элементов заданной цепи. Сложная форма графического способа построения дуальной цепи иллюстрируется на примере:
Из рисунка видно, что исходная цепь (левый рисунок) содержит три независимых контура, внутри которых фиксируются три точки (1, 2 и 3), соответствующие узлам исходной дуальной цепи. Четвертую точку, соответствующую узлу 4, фиксируется в области, внешней по отношению к заданной цепи. Между этими точками проводят пунктирные линии, пересекающие элементы цепи и представляющие собой ветви дуальной цепи; пересекаемые элементы заменяются их аналогами, включенными между соответствующими узлами дуальной цепи. При согласовании ЭДС и токов дуальных источников руководствуются следующим правилом: если ЭДС источника действует в положительном направлении контура (по ходу часовой стрелки), то ток источника тока в дуальной цепи направлен к узлу, соответствующему данному контуру исходной схемы. При соблюдении пропорции комплексное сопротивление цепи, общей для двух смежных контуров схемы, пропорционально комплексной проводимости цепи, соединяющей два соответствующих узла дуальной цепи. Например, в схеме (3)комплексное сопротивление цепи равно: Полагая, что Аналогичная пропорциональность получается и между входным сопротивлением и проводимостью более сложных дуальных цепей. Это свойство используется, в частности, в теории электрических фильтров. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 718. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


 является функцией этих параметров.
является функцией этих параметров.


 (совпадают по фазе)
(совпадают по фазе) (сдвиг по фазе = 0)
(сдвиг по фазе = 0)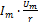 ;
; 

 =
=  =
=  =
=  [Вт]
[Вт]
 всегда ≥ 0 значит, активное сопротивление безвозвратно расходует, поступившую в него электроэнергию.
всегда ≥ 0 значит, активное сопротивление безвозвратно расходует, поступившую в него электроэнергию. =
=  [ Вт ]
[ Вт ]
 ⇒
⇒  =
=  [Дж]
[Дж]

 ;
; 
 , где
, где  - потокосцепление
- потокосцепление 

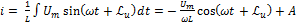 ⊜
⊜ =
= 
 -
- 
 -
- 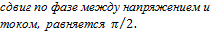

 [Ом] - индуктивное сопротивление
[Ом] - индуктивное сопротивление [См] - индуктивная проводимость
[См] - индуктивная проводимость  , где
, где  – реактивное сопротивление; энергия в виде тепла не выделяется, а периодически накапливается и возвращается обратно в источник; расчетная величина, которая учитывает явления самоиндукции.
– реактивное сопротивление; энергия в виде тепла не выделяется, а периодически накапливается и возвращается обратно в источник; расчетная величина, которая учитывает явления самоиндукции.
 )
)
 =
=
 =
=  [ВAр]
[ВAр]
 >0: энергия потребляется от источника.
>0: энергия потребляется от источника.
 =
= 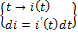 ⇒ полагая, что
⇒ полагая, что  , а
, а  ⇒
⇒ 
 =
= 


 , где
, где 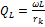 -
- 
 , тем меньше γ и тем ближе реальная катушка к идеальному элементу цепи индуктивности.
, тем меньше γ и тем ближе реальная катушка к идеальному элементу цепи индуктивности.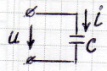

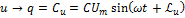
 =
=
 -
- 
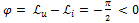 -
- 
 , где
, где  - емкостное сопротивление [Ом]
- емкостное сопротивление [Ом]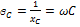 [См] -
[См] - 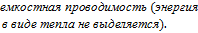



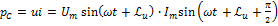 =
=
 =
= 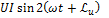 [ВAр]
[ВAр]

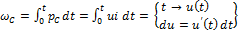
 и
и  ⇒
⇒ 
 =
=  [Дж]
[Дж] 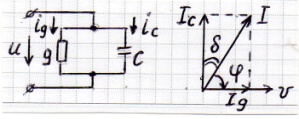


 - добротность реального конденсатора [б/р]
- добротность реального конденсатора [б/р] , тем меньше 𝛿 и тем ближе реальный конденсатор к идеальному элементу цепи емкости.
, тем меньше 𝛿 и тем ближе реальный конденсатор к идеальному элементу цепи емкости.


 ⇒ 𝜑 - ?
⇒ 𝜑 - ? =
= 

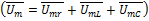
 ← ∆-к напряжений
← ∆-к напряжений  – реактивное
– реактивное – активное
– активное =
= 
 - реактивное сопротивление
- реактивное сопротивление
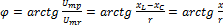
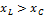 , 𝜑 > 0 ⇒
, 𝜑 > 0 ⇒ 
 , 𝜑 < 0 ⇒
, 𝜑 < 0 ⇒ 
 , 𝜑 < 0 ⇒ в цепи возникает резонанс
, 𝜑 < 0 ⇒ в цепи возникает резонанс 



 =
= 
 -
- 
 –
– 
 , то получится ∆ сопротивления.
, то получится ∆ сопротивления.


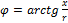


 ;
;  , L, C .
, L, C . 

 ⇒ 𝜑 - ?
⇒ 𝜑 - ? (3)
(3) → закон Ома при
→ закон Ома при  соединении
соединении  , L, C в цепи.
, L, C в цепи.
 - полная проводимость цепи.
- полная проводимость цепи. Элементы электрической цепи:
Элементы электрической цепи: (2)
(2) 



 . Таким образом, контурному току i соответствует узловое напряжение u.
. Таким образом, контурному току i соответствует узловое напряжение u. .
. 
 , а в схеме (4) комплексная проводимость цепи:
, а в схеме (4) комплексная проводимость цепи: 
 где k – коэффициент пропорциональности, имеющий размерность сопротивления, получаем:
где k – коэффициент пропорциональности, имеющий размерность сопротивления, получаем: 