
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теорема 3. Никакие два из множеств
Не равномощны. Д о к а з а т е л ь с т в о. Обозначим Ясно, что Отсюда следует, что множество Повторив это рассуждение достаточное число раз, придем к заключению, что каждое из множеств Теорема 4. Пусть семейство множеств Тогда сумма Д о к а з а т е л ь с т в о. Предположим, что Из теорем 3 и 4 следует, что различных бесконечных кардинальных чисел бесконечно много. Исходя из множества
среди которых (согласно теореме 3) нет ни одной пары равномощных. Таким способом можно получить бесконечно много различных кардинальных чисел. Из аксиомы замены вытекает существование семейства А, элементами которого служат все множества (3). Семейство А в силу теоремы 3 обладает свойством (2). Тогда по теореме 4 мощность суммы 
каждые два множества которой имеют различные мощности и ни одно из них не равномощно никакому из множеств (3). Таким образом, получаем бесконечно много новых кардинальных чисел. Другие кардинальные числа получаем, беря семейство В всех множеств (3) и (4) и строя последовательность
Этот процесс можно продолжать бесконечно. Отсюда видно, что шкала всех бесконечных кардинальных чисел намного богаче шкалы конечных мощностей (которая совпадает со шкалой целых положительных чисел). Отметим дальнейшие следствия теоремы 2. Теорема 5. Не существует такого семейства множеств По теореме 2 множество Теорема 6. Не существует множества всех множеств. В противном случае это множество было бы множеством Теорема 6 снова указывает, что нельзя приянть аксиому, утверждающую существование для каждой высказывательной функции Теорема 5 еще раз подтверждает большое разнообразие кардинальных чисел: их так много, что нельзя образовать множества, содержащего по крайней мере по одному множеству каждой мощности.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 267. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (1)
(1) -е множество этой последовательности символом
-е множество этой последовательности символом  . Предположим, что существуют такие
. Предположим, что существуют такие 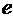 , что
, что  и
и  .
. тогда будет равномощно некоторой части множества
тогда будет равномощно некоторой части множества  , где
, где 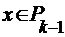 .
. равномощно какому-то подмножеству множества
равномощно какому-то подмножеству множества  .
. обладает свойством: для каждого
обладает свойством: для каждого  существует множество
существует множество  , не ранвомощное никакому подмножеству множества
, не ранвомощное никакому подмножеству множества 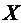 . (2)
. (2) не равномощна никакому
не равномощна никакому 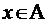 и никакому его подмножеству.
и никакому его подмножеству. . Тогда существует такая взаимно однозначная функция
. Тогда существует такая взаимно однозначная функция  , что
, что  . Согласно (2), существует множество
. Согласно (2), существует множество  , не равномощное никакому подмножеству множества
, не равномощное никакому подмножеству множества  . Т.к.
. Т.к.  , то
, то  , т.е.
, т.е.  , откуда
, откуда 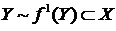 . Это противоречие и доказывает теорему.
. Это противоречие и доказывает теорему.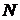 натуральных чисел, имеющего мощность
натуральных чисел, имеющего мощность  , построим множества
, построим множества (3),
(3), отлична от мощностей любого из множеств (3) и их подмножеств. Снова применяя теорему 3, получаем последовательность
отлична от мощностей любого из множеств (3) и их подмножеств. Снова применяя теорему 3, получаем последовательность (4),
(4), .
. , которое для каждого множества
, которое для каждого множества 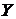 , равномощное множеству
, равномощное множеству  не равномощно никакому подмножеству множества
не равномощно никакому подмножеству множества  и, значит, не равномощно никакому подмножеству
и, значит, не равномощно никакому подмножеству 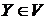 следует
следует  ).
).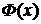 множества, состоящего из элементов, удовлетворяющих этой функции (смотреть главу II, §3).
множества, состоящего из элементов, удовлетворяющих этой функции (смотреть главу II, §3).