
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теорема 2. Любое подмножество счетного множества счетно.Теорема 3. Сумма двух счетных множеств счетна. Д о к а з а т е л ь с т в о. Т.к. случай, когда одно из данных множеств пусто, не представляет трудности, будем считать, что
Тогда сумма Можно доказать по индукции, что сумма любого конечного числа счетных множеств счетно. Следствие 4. Сумма конечного и счетного множества счетна. Теорема 5. Декартово произведение двух счетных множеств счетно. Д о к а з а т е л ь с т в о. Если Если одно из множеств Таким образом, утверждение данной теории следует из теоремы 2. Теорема 7. Если Д о к а з а т е л ь с т в о. По определению Таким образом, °Теорема 8. Если Д о к а з а т е л ь с т в о. Обозначим через Тогда, согласно аксиоме выбора, существует такая последовательность  Замечание. Необходимость применения аксиомы выбора в доказательстве теоремы 8 обусловлена тем, что хотя для каждого множества существует бесконечная последовательность, состоящая из всех его элементов, но для данного множества таких последовательностей бесконечно много и у нас нет способа выделения какой-то одной из них. Другими словами, у нас нет способа сопоставления каждому счетному множеству бесконечной последовательности, содержащей все его элементы. Примеры счетных множеств. Пример 1. Множество целых чисел счетно. Действительно, это множество представляет собой сумму Пример 2. Множество рациональных чисел счетно. В самом деле, последовательность Пример 3. Множество многочленов от одной переменной с целыми коэффицентами счетно. Действительно, каждому многочлену с целыми коэффицентами взаимно однозначно соответствует последовательность его коэффицентов, а множество всех конечных последовательностей целых чисел (согласно теореме 6) счетно. Пример 4. Множество алгебраических чисел счетно. Каждому многочлену соответствует конечная последовательность всех его корней: в качестве первого члена этой последовательности берем корень с наименьшим модулем и с наименьшим аргументом среди всех корней этого модуля; в качестве второго члена берем отличный от первого, с наименьшим возможным модулем и с наименьшим аргументом среди всех корней этого модуля и т.д. Согласно теореме 7, множество всех алгебраических чисел счетно. Этот результат можно получить из теоремы 8, но тогда пришлось бы пользоваться аксиомами выбора.
Шкала кардинальных чисел.
Теперь мы докажем, что кроме конечных кардинальных чисел и числа а существует бесконечно много других кардинальных чисел. Для этого докажем теорему, играющую большую роль во многих разделах теории множеств. Теорема 1 (о диагонали (Кантор)). Если область определения Д о к а з а т е л ь с т в о. Мы должны показать, что В случае
Представим множество если если же Эта интерпритация объясняет название «теоремы о диагонали». Разница в этом предельном случае будет хотя бы в одну точку
Применим теорему 1 для доказательства существования различных бесконечных мощностей. Теорема 2. Множество Д о к а з а т е л ь с т в о. Действительно, в противном случае существовала бы взаимно однозначная функция |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 296. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
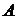 - множество значений последовательности
- множество значений последовательности 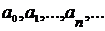 ,
, - множество значений последовательности
- множество значений последовательности 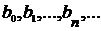 .
.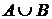 есть множество значений полседовательности
есть множество значений полседовательности 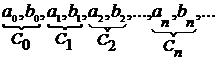 , и поэтому счетно.
, и поэтому счетно.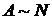 ,
, 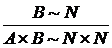 (в силу теоремы 1 §3, глава III).
(в силу теоремы 1 §3, глава III).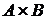 равномощно некоторому подмножеству произведения
равномощно некоторому подмножеству произведения 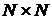 , т.е. подмножеству множества
, т.е. подмножеству множества 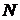 .
.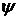 - бесконечная последовательность, члены которой – также бесконечные последовательности, то множество
- бесконечная последовательность, члены которой – также бесконечные последовательности, то множество  элементов x, являющихся членами последовательности
элементов x, являющихся членами последовательности 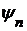 , счетно.
, счетно.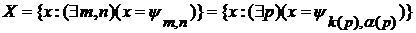 .
.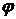 , определенной равенством
, определенной равенством 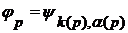 .
.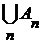 счетна.
счетна.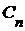 множество последовательностей
множество последовательностей 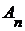 будет множеством значений. По условию
будет множеством значений. По условию 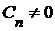 для каждого
для каждого  .
.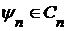 для каждого
для каждого 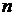 . Таким образом, сумма
. Таким образом, сумма 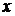 , для которых существуют такие
, для которых существуют такие 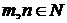 , что
, что 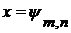 . В силу теоремы 7 это множество счетно.
. В силу теоремы 7 это множество счетно.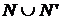 , где
, где 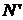 - множество чисел
- множество чисел 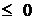 . Т.к.
. Т.к. 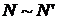 (равномощность этих множеств устанавливает функция
(равномощность этих множеств устанавливает функция 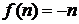 ), то множество
), то множество 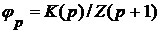 , содержит в качестве своих членов все положительные рациональные числа и только их. Значит, множество всех положительных рациональных чисел счетно, и поэтому (смотреть пример 1) множество всех рациональных чисел также счетно.
, содержит в качестве своих членов все положительные рациональные числа и только их. Значит, множество всех положительных рациональных чисел счетно, и поэтому (смотреть пример 1) множество всех рациональных чисел также счетно. функции
функции 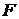 содержится в
содержится в  не является значением функции
не является значением функции  для всех
для всех 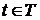 . Из определения множества
. Из определения множества 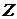 следует, что для
следует, что для 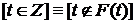 . Если
. Если 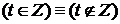 .
.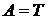 теорема 1 имеет наглядную геометрическую интерпритацию.
теорема 1 имеет наглядную геометрическую интерпритацию.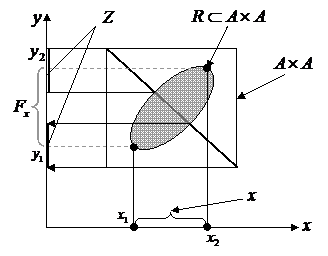

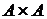 в виде квадрата (смотреть главу II, §4) и рассмотрим в нем множество
в виде квадрата (смотреть главу II, §4) и рассмотрим в нем множество 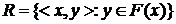 . Тогда
. Тогда 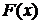 - проекция на ось одинат
- проекция на ось одинат 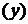 тех точек из
тех точек из  , абсциссы которых равны
, абсциссы которых равны 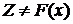 для всех
для всех 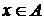 . В самом деле :
. В самом деле :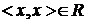 , то
, то 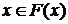 , но
, но 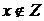 ,
,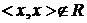 , то
, то 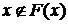 , но
, но 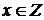 .
.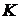 .
.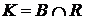 ,
, 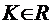 ,
, 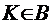 .
.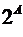 не равномощно ни самому
не равномощно ни самому  , ни его подмножеству.
, ни его подмножеству. с областью определения в
с областью определения в