
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Модели стационарных временных рядовЧасто экономические показатели, представленные временными рядами, имеют настолько сложную структуру, что моделирование таких рядов путем построения моделей тренда, сезонности и применения традиционных подходов не приводит к удовлетворительным результатам. Во временных рядах остатков прослеживаются статистические зависимости, которые можно моделировать. В последнее время большое внимание уделяется моделированию стационарных временных рядов, т.к. многие временные ряды могут быть приведены к стационарному виду после операции выделения тренда, фильтрации сезонной компоненты или взятия разности. Как правило, ряд остатков – это стационарный ряд. Наиболее распространенные модели стационарных рядов – модели авторегрессии и модели скользящего среднего.
Авторегрессионные модели. В авторегрессии каждое значение ряда находится в линейной зависимости от предыдущих значений. Если анализируемый динамический процесс зависит от значений, отстоящих на p временных лагов назад, то авторегрессионный процесс порядка p, т.е. AR(p):
где
Используя функцию оператора лага, можно представить авторегрессионную модель в виде:
где Ф( Для выполнения условия стационарности все корни многочлена Ф(  Рассмотрим простейший вариант линейного авторегрессионного процесса – модель авторегрессии 1-го порядка – AR(1), или марковский процесс[22]. Эта модель может быть представлена в виде:
где
Основные свойства Марковского процесса:
Значения частной автокорреляционной функции равны нулю для всех лагов Условие стационарности ряда для AR(1) определяется требованием к коэффициенту Из авторегрессионных процессов выше первого порядка в экономической практике часто встречаются так называемые процессы Юла. Они описываются с помощью модели AR(2):
Выражение для вычисления любого значения АКФ
Подставим в данное выражение значение
Эта система называется системой Юла – Уокера для AR(2). Из нее можно получить выражения для определения параметров
Условия стационарности процесса AR(2):
ЧАКФ для процесса AR(p) будет иметь ненулевые значения лишь при
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 494. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
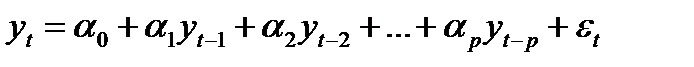 (8.7)
(8.7)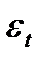 – «белый шум» с
– «белый шум» с 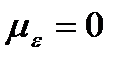 ;
;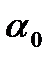 – свободный член (часто приравнивается к нулю (опускается)).
– свободный член (часто приравнивается к нулю (опускается)).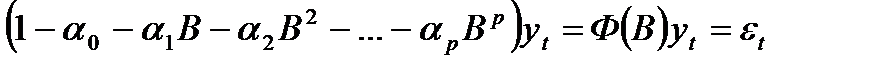 ,
,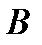 - оператор сдвига, т.е. преобразование ряда, смещающего его на один временной такт;
- оператор сдвига, т.е. преобразование ряда, смещающего его на один временной такт;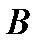 ) – оператор авторегрессии.
) – оператор авторегрессии.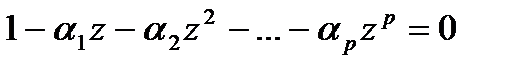 должны быть по модулю больше 1 и различны, т.е.
должны быть по модулю больше 1 и различны, т.е. 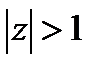 . Если
. Если 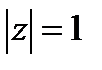 , процесс называется процессом единичного корня и является нестационарным.
, процесс называется процессом единичного корня и является нестационарным.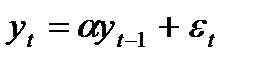 , (8.8)
, (8.8)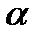 - числовой коэффициент,
- числовой коэффициент, 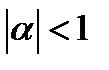 ,
,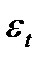 - последовательность случайных величин, образующих белый шум.
- последовательность случайных величин, образующих белый шум.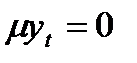 ;
;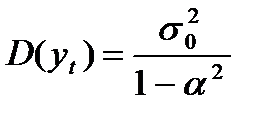 ; (8.9)
; (8.9)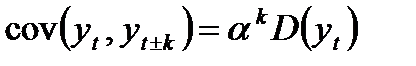 ;
;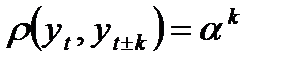 .
.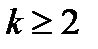 , что может быть использовано при подборе модели. Этот результат для теоретической ЧАКФ и может не выполняться для выборочной АКФ. Однако, если выборочные частные корреляции статистически незначимо отличаются от нуля при
, что может быть использовано при подборе модели. Этот результат для теоретической ЧАКФ и может не выполняться для выборочной АКФ. Однако, если выборочные частные корреляции статистически незначимо отличаются от нуля при 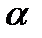 :
: 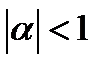 .
.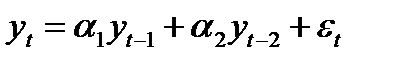 (8.10)
(8.10)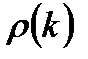 :
: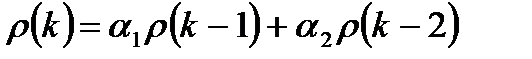 . (8.11)
. (8.11)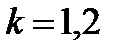 . С учетом того, что
. С учетом того, что 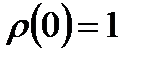 , а
, а 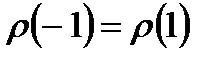 , получим:
, получим: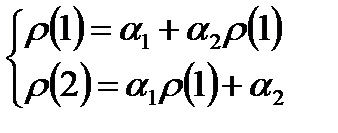 (8.12)
(8.12)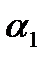 и
и 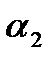 :
: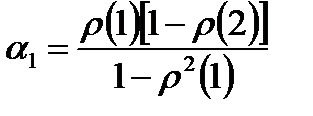 (8.13)
(8.13)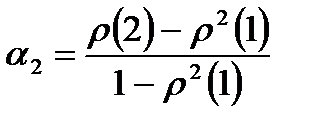 . (8.14)
. (8.14)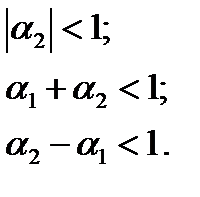 (8.15)
(8.15)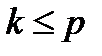 , а начиная с лага
, а начиная с лага 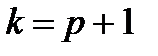 теоретическая ЧАКФ равна нулю. Это свойство становится ключевым при подборе порядка p авторегрессионной модели для конкретных экономических временных рядов.
теоретическая ЧАКФ равна нулю. Это свойство становится ключевым при подборе порядка p авторегрессионной модели для конкретных экономических временных рядов.