
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Доверительные границы трендаЕсли уравнение тренда рассматривается как выборочное, имеющее ошибки репрезентативности своих параметров, то можно рассчитать доверительные границы, внутри которых с заданной, достаточно большой вероятностью, проходит линия тренда в генеральной совокупности. Рассмотрим эту проблему на примере простейшего, линейного тренда. Оба его параметра, свободный член
Средняя ошибка репрезентативности параметра
Свободный член уравнения линейного тренда и среднее изменение за единицу времени – величины независимые, а, следовательно, по теореме сложения дисперсий независимых величин, дисперсия их суммы равна сумме дисперсий слагаемых, а среднее квадратическое отклонение (средняя ошибка) – корню квадратному из суммы дисперсий, то есть из суммы квадратов ошибок 
(5.15)
при Таким образом, ошибка тренда возрастает от середины базы его расчета (середина ряда) к его краям, образуя конусообразную зону вероятных значений генерального тренда (рис. 1.4)
Рис. 1.4. Доверительные границы генерального тренда
Чем сильнее колеблемость уровней и чем меньше база расчета тренда, тем шире доверительная зона генерального тренда, и тем быстрее она расширяется от середины ряда к его концам. Зона для параболического тренда расширятся при этом гораздо сильнее, чем для линейного тренда[14].
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 479. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и среднее изменение за единицу времени
и среднее изменение за единицу времени  имеют ошибки репрезентативности выборочных оценок. Свободный член уравнения тренда - это выборочная средняя величина уровней временного ряда, средняя ошибка репрезентативности которой
имеют ошибки репрезентативности выборочных оценок. Свободный член уравнения тренда - это выборочная средняя величина уровней временного ряда, средняя ошибка репрезентативности которой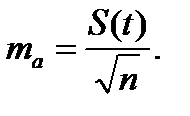 (5.13)
(5.13) (5.14)
(5.14) и
и  . Однако, мы рассматриваем ошибку не в статике, а в динамике. Средняя ошибка положения линии тренда за счет ошибки свободного члена – это константа для любой точки линии тренда, а средняя ошибка изменения уровня тренда за счет ошибки параметра
. Однако, мы рассматриваем ошибку не в статике, а в динамике. Средняя ошибка положения линии тренда за счет ошибки свободного члена – это константа для любой точки линии тренда, а средняя ошибка изменения уровня тренда за счет ошибки параметра 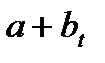 , и ошибка параметра
, и ошибка параметра  раз по сравнению с ошибкой в точке, где
раз по сравнению с ошибкой в точке, где  . Иначе говоря, ошибка линии тренда минимальна в середине базы его расчета – в середине временного ряда. В этой точке, где
. Иначе говоря, ошибка линии тренда минимальна в середине базы его расчета – в середине временного ряда. В этой точке, где  , средняя ошибка положения линии тренда равна ошибке его свободного члена, т.е.
, средняя ошибка положения линии тренда равна ошибке его свободного члена, т.е. 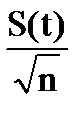 , а в любой иной точке тренда его средняя ошибка вычисляется по формуле:
, а в любой иной точке тренда его средняя ошибка вычисляется по формуле:
 в середине ряда. При нумерации периодов времени от начала ряда вместо
в середине ряда. При нумерации периодов времени от начала ряда вместо  в формулу следует подставить величину
в формулу следует подставить величину  .
.